La prueba de Kolmogorov es una prueba de bondad de ajuste, es decir, del grado en que la distribución observada difiere de otra distribución. Es una alternativa a la prueba Ji Cuadrado de bondad de ajuste cuanto el número de datos es pequeño. La prueba no debe ser aplicada si hay muchos empates.

a) Supuestos. Los datos están medidos al menos a nivel ordinal.

b) Hipótesis Nula: No hay diferencias entre las distribuciones comparadas.

c) Estadístico de contraste: D (mayor diferencia entre las frecuencias relativas de las distribuciones).

d) Distribución del estadístico de contraste: Específico dependiendo de la distribución con que se compare la distribución observada.

 

Ejemplo

Desean saber si una muestra de debe datos pertenece a una población normalmente distribuida. Los datos (ordenados de menor a mayor) son:

b) Hipótesis Nula: No hay diferencia estadísticamente significativa entre la distribución de la población a que pertenece la muestra y la distribución Normal.

Hipótesis Alternativa: Hay diferencia estadísticamente significativa entre la distribución de la población a que pertenece la muestra y la distribución Normal.

c) Estadístico de contraste. Obtención del estadístico de contraste:

Tipificar la muestra:

Obtener los valores típicos que corresponden a diez intervalos de una distribución Normal:

 

-1.28, -0.84, -0.52, -0.25, 0, 0.25, 0.52, 0.84, 1.28

(Valores que corresponden a los puntos cuya función de distribución Normal estandarizada son 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8 y 0.9)

Emparejar las distribuciones tipificadas hipotética (Normal en el ejemplo) y observada:

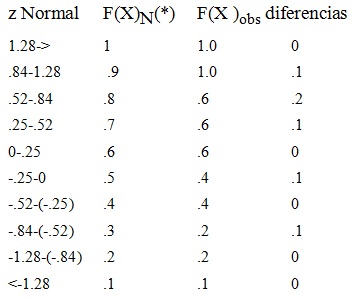
(Notas:

* F(X) se refiere al límite superior del intervalo.

* Los valores en la columna F(X)obs son funciones de la distribución Normal estandarizada y son los que correspondería a las puntuaciones observadas si ajustaran a la distribución Normal, es decir, si la Hipótesis Nula fuera verdadera)

D=0.2

e) Significación del estadístico de contraste: De acuerdo con las tablas de la prueba es igual a 0.81

f) Se acepta la Hipótesis Nula por ser mayor la significación del estadístico de contraste que el nivel previamente establecido (alfa= 0.05)