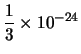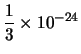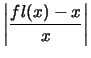Next: 3.3.2 Las operaciones básicas
Up: 3.3 Aritmética de punto
Previous: 3.3 Aritmética de punto
Estamos interesados en estimar el error en que se incurre al aproximar
un número real positivo x mediante un número de máquina del
MARC-32. Si representamos el número mediante:
en donde cada ai es 0 ó 1 y el bit principal es a1
= 1. Un número de máquina se puede obtener de dos formas:
- Truncamiento: descartando todos los bits excedentes
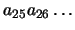 .
El número resultante, x' es siempre menor que
x (se encuentra a la izquierda de x en la recta real).
.
El número resultante, x' es siempre menor que
x (se encuentra a la izquierda de x en la recta real).
- Redondeo por exceso: Aumentamos en una unidad el último
bit remanente a24 y después eliminamos el exceso de bits como
en el caso anterior.
Todo lo anterior, aplicado al caso del MARC-32, se resume
diciendo que si x es un número real distinto de 0 dentro del
intervalo de la máquina, entonces el número de máquina x* más
cercano a x satisface la desigualdad:
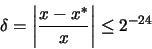 |
(20) |
que se puede escribir de la siguiente forma:
Ejemplo 6: ¿Cómo se expresa en binario el número x = 2/3? ¿Cuáles
son los números de máquina x' y x'' próximos en el
MARC-32?
El número 2/3 en binario se expresa como:
Los dos números de máquina próximos, cada uno con 24 bits, son:
| x' |
= |
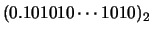 |
|
| x'' |
= |
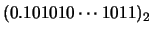 |
|
en donde x' se ha obtenido por truncamiento y x'' mediante
redondeo por exceso. Calculamos ahora las diferencias x - x' y x''
- x para estimar cual es el error cometido:
| x - x' |
= |
 |
|
| x'' - x |
= |
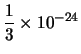 |
|
Por tanto, el número más próximo es
fl(x) = x'' y los errores de
redondeo absoluto y relativo son:
| |fl(x) - x| |
= |
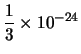 |
|
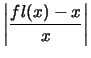 |
= |
2-25 < 2-24 |
|



Next: 3.3.2 Las operaciones básicas
Up: 3.3 Aritmética de punto
Previous: 3.3 Aritmética de punto
Wladimiro Diaz Villanueva
1998-05-11