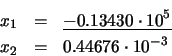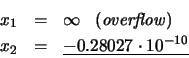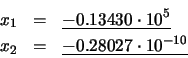Next: 3.4 Desbordamiento por exceso
Up: 3.3 Aritmética de punto
Previous: 3.3.1 Números de máquina
Vamos a analizar el resultado de operar sobre dos números en punto
flotante normalizado de l-dígitos de longitud, x e y, que
producen un resultado normalizado de l-dígitos. Expresaremos esta
operación como:
en donde op es +, -, 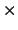 ó
ó 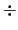 .
Supondremos que en
cada caso la mantisa del resultado es primero normalizada y después
redondeada (operación que puede dar lugar a un desbordamiento que
requeriría renormalizar el número). El valor de la mantisa redondeada
a p bits, qr, se define como (de una forma más rigurosa que en
el caso anterior):
.
Supondremos que en
cada caso la mantisa del resultado es primero normalizada y después
redondeada (operación que puede dar lugar a un desbordamiento que
requeriría renormalizar el número). El valor de la mantisa redondeada
a p bits, qr, se define como (de una forma más rigurosa que en
el caso anterior):
en donde la función redondeo por defecto
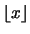 es el mayor entero menor o igual a x y la función
redondeo por exceso
es el mayor entero menor o igual a x y la función
redondeo por exceso
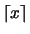 es el menor entero
mayor o igual a x. Para números enteros, esta función se traduce en
la bien conocida regla de sumar 1 en la posición p + 1. Teniendo en
cuenta sólo la mantisa, redondear de este modo da lugar a un intervalo
máximo del error de:
es el menor entero
mayor o igual a x. Para números enteros, esta función se traduce en
la bien conocida regla de sumar 1 en la posición p + 1. Teniendo en
cuenta sólo la mantisa, redondear de este modo da lugar a un intervalo
máximo del error de:
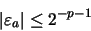 |
(21) |
y un error relativo máximo en el intervalo:
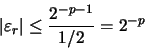 |
(22) |
Analizaremos ahora el error generado por cada una de las operaciones
básicas:
- Multiplicación.
- La operación de multiplicar dos números
expresados en punto flotante implica sumar los exponentes y
multiplicar las mantisas. Si la mantisa resultante no está
normalizada, se recurre a renormalizar el resultado ajustando
adecuadamente el exponente. Después, es necesario redondear la
mantisa a p bits. Para analizar el error de esta operación
supongamos dos números:
Tenemos entonces que el producto será:
xy = qx qy 2fx + fy
en donde el valor de la mantisa se encontrará en el rango:
ya que tanto x como y satisfacen la
ecuación (19). Por tanto, la normalización del
producto
qx qy implica un desplazamiento a la derecha de,
como máximo, una posición. La mantisa redondeada será entonces uno
de estos dos posibles valores:
en donde
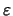 ,
que es el error de redondeo,
cumple la ecuación (21). Tenemos entonces:
,
que es el error de redondeo,
cumple la ecuación (21). Tenemos entonces:
en donde, de acuerdo con la ecuación (22),
tenemos:
Por tanto, la cota del error relativo en la multiplicación es la
misma que la que surge por redondear la mantisa.
- División.
- Para llevar a cabo la división en punto
flotante, se divide la mitad de la mantisa del numerador por la
mantisa del denominador (para evitar cocientes mayores de la
unidad), mientras que los exponentes se restan. Esto es:
Puesto que ambas mantisas satisfacen la
ecuación (18), el valor del cociente estará acotado
entre los límites:
Aplicando un análisis similar al empleado en el caso de la
multiplicación, obtenemos:
en donde, de acuerdo con la ecuación (22),
tenemos:
Es decir, la cota máxima del error relativo en la división, como en
el caso anterior, es la misma que la que surge por redondear la
mantisa.
- Adición y sustracción.
- La operación de suma o resta se
realiza del siguiente modo: se toma la mantisa del operando de menor
magnitud (supongamos que es y) y se desplaza
fx - fy posiciones a la derecha. La mantisa resultante es sumada (o restada)
y el resultado se normaliza y después se redondea. Es decir:
El análisis del error cometido en esta operación es más
complejo que los estudiados hasta ahora, por lo que no lo vamos a
ver en detalle. Sin embargo, el resultado final indica que la cota
máxima del error cometido en la adición y la sustracción viene dado
por:
En conclusión, en todas las operaciones aritméticas elementales en
punto flotante, el error absoluto del resultado es no mayor de 1 en el
bit menos significativo de la mantisa.
Sin embargo, los errores de redondeo se acumulan a medida que aumenta
el número de cálculos. Si en el proceso de calcular un valor se llevan
a cabo N operaciones aritméticas es posible obtener, en el mejor de
los casos, un error de redondeo total del orden de
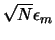 4 (que coincide con el caso en que los errores de
redondeo están aleatoriamente distribuidos, por lo que se produce una
cancelación parcial). Desafortunadamente, este error puede crecer muy
rápidamente por dos motivos:
4 (que coincide con el caso en que los errores de
redondeo están aleatoriamente distribuidos, por lo que se produce una
cancelación parcial). Desafortunadamente, este error puede crecer muy
rápidamente por dos motivos:
- Es muy frecuente que la regularidad del cálculo o las
peculiaridades del computador den lugar a que el error se acumule
preferentemente en una dirección; en cuyo caso el error de redondeo
se puede aproximar a
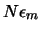 .
.
- En circunstancias especialmente desfavorables pueden existir
operaciones que incremente espectacularmente el error de redondeo.
Generalmente, este fenómeno se da cuando se calcula la diferencia
entre dos números muy próximos, dando lugar a un resultado en el
cual los únicos bits significativos que no se cancelan son los de
menor orden (en los únicos en que difieren). Puede parecer que la
probabilidad de que se de dicha situación es pequeña, sin embargo,
algunas expresiones matemáticas fomentan este fenómeno.
Veamos con un ejemplo los problemas comentados anteriormente. Hay dos
formas de calcular las soluciones de la familiar ecuación cuadrática:
ax2 + bx + c = 0
que son:
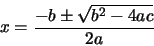 |
(23) |
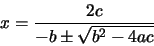 |
(24) |
Cualquiera de estas dos expresiones da problemas cuando a, c o
ambos, son pequeños. En estos casos, el valor del discriminante es muy
próximo al valor de b:
por lo que la diferencia
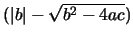 viene afectada de
un error de redondeo importante. En efecto, la ecuación (23)
evalúa bien la raíz más grande en valor absoluto, pero da pésimos
resultados al estimar la raíz menor en valor absoluto. Por otra parte,
la ecuación (24) calcula bien la raíz menor (siempre en
valor absoluto) pero no la raíz más grande.
viene afectada de
un error de redondeo importante. En efecto, la ecuación (23)
evalúa bien la raíz más grande en valor absoluto, pero da pésimos
resultados al estimar la raíz menor en valor absoluto. Por otra parte,
la ecuación (24) calcula bien la raíz menor (siempre en
valor absoluto) pero no la raíz más grande.
La solución del problema pasa por emplear una expresión mejor
condicionada. En este caso, es preferible calcular previamente:
![\begin{displaymath}
q = -\frac{1}{2} \left[b + \mathrm{sign}(b) \sqrt{b^{2} - 4ac}
\right]
\end{displaymath}](img111.gif) |
(25) |
y las dos raíces a partir de valor de q como:
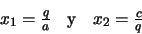 |
(26) |
Ejemplo: Calcular las raíces de la siguiente ecuación cuadrática:
ax2 + bx + c = 0
siendo:
Solución: Empleando la ecuación (23), obtenemos:
Sin embargo, empleando la expresión (24):
Por último, empleando las expresiones (25)
y (26) se obtienen ambas soluciones correctas:



Next: 3.4 Desbordamiento por exceso
Up: 3.3 Aritmética de punto
Previous: 3.3.1 Números de máquina
Wladimiro Diaz Villanueva
1998-05-11
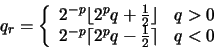
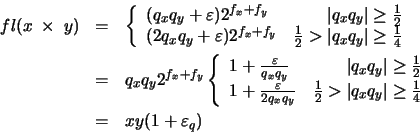
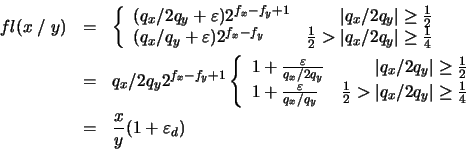
![]() 4 (que coincide con el caso en que los errores de
redondeo están aleatoriamente distribuidos, por lo que se produce una
cancelación parcial). Desafortunadamente, este error puede crecer muy
rápidamente por dos motivos:
4 (que coincide con el caso en que los errores de
redondeo están aleatoriamente distribuidos, por lo que se produce una
cancelación parcial). Desafortunadamente, este error puede crecer muy
rápidamente por dos motivos: