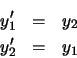
La mejor forma de ver este fenómeno es a través de un ejemplo. Supongamos el siguiente sistema de ecuaciones diferenciales:
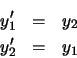
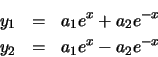
es posible determinar que el valor de las constantes a1 y a2 es: a1 = 0 & y & a2 = 1
Hasta este punto, las soluciones son exactas. Sin embargo, supongamos
que el sistema de ecuaciones anterior se resuelve empleando un método
numérico cualquiera con el fin de calcular los valores de las funciones
y1 y y2 en una secuencia de puntos ![]() y que el error del método da lugar a un valor de
y que el error del método da lugar a un valor de ![]() .
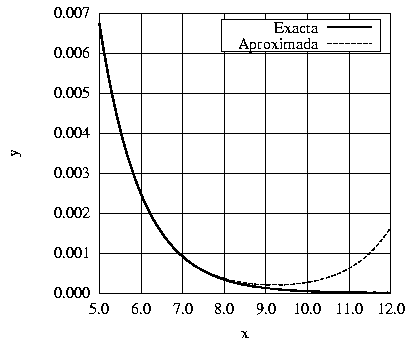
Ya que a1 multiplica a un exponencial creciente cualquier
valor, por pequeño que sea, de a1 dará
lugar a que el término ex domine sobre el término
e-x para valores suficientemente grandes de x
(ver figura (2)). La conclusión
que se obtiene es que no es posible calcular una solución al sistema
de ecuaciones diferenciales anterior que, para valores suficientemente
grandes de x, no de lugar a un error arbitrariamente grande en relación
con la solución exacta.
.
Ya que a1 multiplica a un exponencial creciente cualquier
valor, por pequeño que sea, de a1 dará
lugar a que el término ex domine sobre el término
e-x para valores suficientemente grandes de x
(ver figura (2)). La conclusión
que se obtiene es que no es posible calcular una solución al sistema
de ecuaciones diferenciales anterior que, para valores suficientemente
grandes de x, no de lugar a un error arbitrariamente grande en relación
con la solución exacta.
|
|
El problema anterior se dice que es inherentemente inestable, o empleando una terminología más común en cálculo numérico, se dice que está 'mal condicionado' (ill-conditioned).