6.1.5 Pivoteo

Sin embargo, los algoritmos de Gauss y Gauss-Jordan que acabamos de describir pueden dar lugar a resultados erróneos fácilmente. Por ejemplo, analicemos el siguiente sistema de ecuaciones, en el que $\epsilon$ es un número muy pequeño pero distinto de cero:

$$\begin{array}{llll} \left( \begin{array}{cc} \epsilon & 1 ... ...eft( \begin{array}{c} 1 \\ 2 \end{array} \right) \end{array}$$

Al aplicar el algoritmo gaussiano se obtiene el siguiente sistema triangular superior:

$$\begin{array}{llll} \left( \begin{array}{cc} \epsilon & 1 ... ...rray}{c} 1 \\ 2-\epsilon^{-1} \end{array} \right) \end{array}$$

y la solución es:

$$\left\{ \begin{array}{l} x_{2} = \frac{2-\epsilon^{-1}}{1-\... ...^{-1}} \\ x_{1} = (1-x_{2})\epsilon^{-1} \end{array}\right.$$

En el computador, si $\epsilon$ es suficientemente pequeño, los términos $2-\epsilon^{-1}$ y $1-\epsilon^{-1}$ se computarán como un mismo número, por lo que $x_{2} \approx 1$ y $x_{1} \approx 0$. Sin embargo, la solución correcta es:

$$\left\{ \begin{array}{l} x_{1} = \frac{1}{1-\epsilon} \appr... ...= \frac{1-2\epsilon}{1-\epsilon} \approx 1 \end{array}\right.$$

Tenemos entonces que la solución calculada es exacta para x₂ pero extremadamente inexacta para x₁.

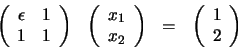
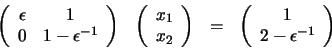
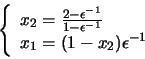
El problema anterior no radica en la pequeñez del término a_ii, sino en su pequeñez relativa respecto de los otros elementos de su fila. La conclusión que podemos extraer es que un buen algoritmo debe incluir el intercambio de ecuaciones cuando las circunstancias así lo exijan. Un algoritmo que cumple este requisito es el denominado eliminación gaussiana con pivoteo de filas escaladas.