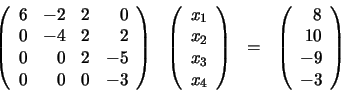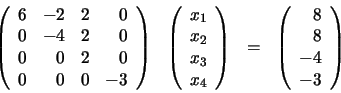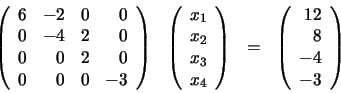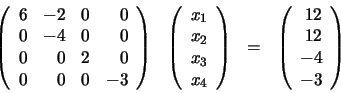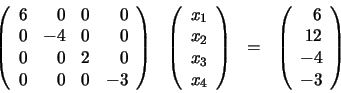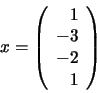Next: 6.1.5 Pivoteo
Up: 6.1 Métodos de resolución
Previous: 6.1.3 Eliminación gaussiana básica
6.1.4 Método de Gauss-Jordan
Como hemos visto, el método de Gauss transforma la matriz de
coeficientes en una matriz triangular superior. El método de
Gauss-Jordan continúa el proceso de transformación hasta obtener una
matriz diagonal unitaria (aij=0 para cualquier 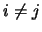 ).
).
Veamos el método de Gauss-Jordan siguiendo con el ejemplo empleado en
el apartado anterior. Aplicando el método de Gauss habíamos llegado a
la siguiente ecuación:
Ahora seguiremos un procedimiento similar al empleado en el método de
Gauss. Tomaremos como pivote el elemento a44=-3; multiplicamos la
cuarta ecuación por
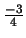 y la restamos a la primera:
y la restamos a la primera:
Realizamos la misma operación con la segunda y tercera fila,
obteniendo:
Ahora tomamos como pivote el elemento a33=2, multiplicamos la
tercera ecuación por
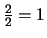 y la restamos a la primera:
y la restamos a la primera:
Repetimos la operación con la segunda fila:
Finalmente, tomamos como pivote a22=-4, multiplicamos la segunda
ecuación por
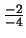 y la sumamos a la primera:
y la sumamos a la primera:
El sistema de ecuaciones anterior es, como hemos visto, fácil
de resolver. Empleando la ecuación (46) obtenemos las
soluciones:



Next: 6.1.5 Pivoteo
Up: 6.1 Métodos de resolución
Previous: 6.1.3 Eliminación gaussiana básica
Wladimiro Diaz Villanueva
1998-05-11
![]() ).
).
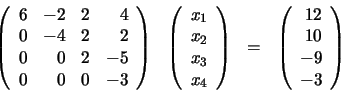
![]() y la restamos a la primera:
y la restamos a la primera: