-μ(
-μ( ))/σ(
))/σ( ) ,
) ,| ( |
n m |
) =
|
n(n-1)(n-2)...(n-(m-1))
m! |
= |
n!
m!(n-m)! |
(combinaciones
de n sobre m) |
| PB(m)
= ( |
n m |
)
pm
qn-m (distribución
binomial B(p,n)) |
 (distribución
multinomial)
(distribución
multinomial)| Teorema -1.2:
(a+b)n
= |
n ∑ . m=0. |
( | n m |
) am
bn-m (binomio
de Newton) |
| Teorema 1.2: |
n ∑ . m=0. |
PB(m) = 1. |
| Teorema 1.3:
para
todo m=1...n, ( |
n m |
)·m = n·( | n-1 m-1 |
) |
| Teorema 1.5:
para
todo m=2...n, m·( |
n-1 m-1 |
) = (n-1)·( | n-2 m-2 |
) + ( | n-1 m-1 |
) |
| Teorema -1.5: eμ = | ∞ ∑ m=0. |
μm/m! (desarrollo en serie de Taylor del exponencial) |
| Teorema 1.7: | ∞ ∑ m=0. |
PΠ(m) = 1. |
 o la desviación típica
muestral s(X)
[naturalmente, para los estadisticos se cumplen la mismas relaciones
que para los parámetros poblacionales correspondientes]. Y
llamamos distribución
muestral a la distribución de un estadístico en el
conjunto de todas las muestras de la población de un cierto
tamaño n. Los parámetros poblacionales de la
distribución muestral, como la media de las medias μ(
o la desviación típica
muestral s(X)
[naturalmente, para los estadisticos se cumplen la mismas relaciones
que para los parámetros poblacionales correspondientes]. Y
llamamos distribución
muestral a la distribución de un estadístico en el
conjunto de todas las muestras de la población de un cierto
tamaño n. Los parámetros poblacionales de la
distribución muestral, como la media de las medias μ( ),
la varianza de las medias σ2(
),
la varianza de las medias σ2( ) o la
media de las varianzas μ(s2(X)),
son
importantes para realizar estimaciones a partir del estadístico
de una muestra sobre el correspondiente parámetro poblacional. A
tal efecto, hay que tener en cuenta las siguientes relaciones:
) o la
media de las varianzas μ(s2(X)),
son
importantes para realizar estimaciones a partir del estadístico
de una muestra sobre el correspondiente parámetro poblacional. A
tal efecto, hay que tener en cuenta las siguientes relaciones: )=μ(X)
)=μ(X) )=σ2(X)/n
si las muestras son con reemplazamiento o la población es
infinita (aproximadamente, si es muy grande).
)=σ2(X)/n
si las muestras son con reemplazamiento o la población es
infinita (aproximadamente, si es muy grande). -μ(
-μ( ))/σ(
))/σ( ) ,
) , y
de la desviación típica s(X) en el conjunto de alumnos de
la asignatura, comenzaremos estimando la desviación
típica σ(X) de la población mediante la desviación
típica corregida
y
de la desviación típica s(X) en el conjunto de alumnos de
la asignatura, comenzaremos estimando la desviación
típica σ(X) de la población mediante la desviación
típica corregida 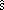 (X) para ser
insesgada. A partir del valor
estimado de σ(X) calcularemos la desviación típica
σ(
(X) para ser
insesgada. A partir del valor
estimado de σ(X) calcularemos la desviación típica
σ( )
de la distribución muestral mediante
la
fórmula de la Actividad 2.2. De la tabla
de la distribución t de Student obtendremos el coeficiente
de confianza t0'80(ν)
(deberemos fijarnos en
la figura que encabeza la tabla para determinar cuál es la
columna que corresponde a dicho coeficiente de confianza). Y finalmente
utilizaremos la expresión de la media t de la correspondiente
variable aleatoria normalizada y la condición
)
de la distribución muestral mediante
la
fórmula de la Actividad 2.2. De la tabla
de la distribución t de Student obtendremos el coeficiente
de confianza t0'80(ν)
(deberemos fijarnos en
la figura que encabeza la tabla para determinar cuál es la
columna que corresponde a dicho coeficiente de confianza). Y finalmente
utilizaremos la expresión de la media t de la correspondiente
variable aleatoria normalizada y la condición | Ejercicio
2.6: estudiar la correlación lineal en el caso |
|
¿X e Y
son
independientes? |
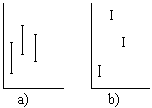 Actividad
2.5. estos procedimientos sean equivalentes la
dispersión
entre las muestras deberá ser proporcionada a la
dispersión
dentro de cada Si tenemos un
conjunto de muestras independientes obtenidas por diferentes
procedimientos,
en caso de que muestra (figura a). A fin de evaluarlo
trabajaremos con m muestras de tamaño n y llamaremos:
Actividad
2.5. estos procedimientos sean equivalentes la
dispersión
entre las muestras deberá ser proporcionada a la
dispersión
dentro de cada Si tenemos un
conjunto de muestras independientes obtenidas por diferentes
procedimientos,
en caso de que muestra (figura a). A fin de evaluarlo
trabajaremos con m muestras de tamaño n y llamaremos: j
y s(Xj
j
y s(Xj a
la
media
de la muestra de tamaño m·n resultante
de mezclar
las m muestras de tamaño n.
a
la
media
de la muestra de tamaño m·n resultante
de mezclar
las m muestras de tamaño n. =
∑
j
=
∑
j  j/m
.
j/m
.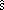 w2
= sw2·n/(n-1),
que
será un estimador insesgado de la varianza
poblacional σ2
.
w2
= sw2·n/(n-1),
que
será un estimador insesgado de la varianza
poblacional σ2
. j-
j- )2/m
= ∑ j
)2/m
= ∑ j  j2/m
-
j2/m
-  2
.
2
. j)2=σ2/n
, σ(
j)2=σ2/n
, σ( )2=σ2/(mn),
demostrar
)2=σ2/(mn),
demostrar j2)
= σ2/n +
(μ+αj)2.
j2)
= σ2/n +
(μ+αj)2. 2)
= σ2/(mn) +
μ2.
2)
= σ2/(mn) +
μ2.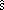 b2
= sb2·nm/(m-1)
.
b2
= sb2·nm/(m-1)
.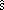 b2)
= σ2 +
n·∑ j αj2/(m-1)
.
b2)
= σ2 +
n·∑ j αj2/(m-1)
.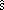 b2
será un estimador insesgado de la varianza
poblacional σ2
si y sólo si las poblaciones a las cuales pertenecen las
diferentes muestras
tienen todas la misma media (lo que llamamos hipótesis
nula en
la que todo αj =0),
cosa que naturalmente
pasará si todas las muestras pertenecen a la misma
población. En este caso, F=
b2
será un estimador insesgado de la varianza
poblacional σ2
si y sólo si las poblaciones a las cuales pertenecen las
diferentes muestras
tienen todas la misma media (lo que llamamos hipótesis
nula en
la que todo αj =0),
cosa que naturalmente
pasará si todas las muestras pertenecen a la misma
población. En este caso, F=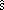 b2/
b2/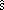 w2
deberá ser próximo a la unidad. En otro caso μ(
w2
deberá ser próximo a la unidad. En otro caso μ(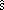 b2)>σ2
, y por lo tanto se puede prever que F sea mayor que la unidad.
b2)>σ2
, y por lo tanto se puede prever que F sea mayor que la unidad. 1,
1,
 2,...
2,... m),
de tamaño m, y que σ(
m),
de tamaño m, y que σ( j)2=σ2/n,
demostrar que si las muestras pertenecen a la misma población
se cumple el
j)2=σ2/n,
demostrar que si las muestras pertenecen a la misma población
se cumple el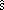 b2/
b2/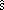 w2
tiene una distribución F de Snedecor con grados de libertad ν1=m-1,
ν2=m·(n-1)
.
w2
tiene una distribución F de Snedecor con grados de libertad ν1=m-1,
ν2=m·(n-1)
.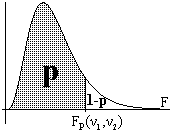 Actividad
2.13. Si tenemos m muestras independientes de tamaño
n y
Actividad
2.13. Si tenemos m muestras independientes de tamaño
n y  b2/
b2/ w2
> Fp(m-1
, m·(n-1)), siendo Fp(ν1, ν2)
el coeficiente crítico de la distribución F de Snedecor
con grados de libertad ν1
y ν2 tal
que la probabilidad de un valor menor o igual a este coeficiente sea
p, entonces podemos rechazar con un nivel de significación
β=1-p la hipótesis nula de que las
muestras pertenezcan a la misma población. Utilizaremos las tablas
de la distribución F de Snedecor (inversa) para
determinar el correspondiente coeficiente crítico.
w2
> Fp(m-1
, m·(n-1)), siendo Fp(ν1, ν2)
el coeficiente crítico de la distribución F de Snedecor
con grados de libertad ν1
y ν2 tal
que la probabilidad de un valor menor o igual a este coeficiente sea
p, entonces podemos rechazar con un nivel de significación
β=1-p la hipótesis nula de que las
muestras pertenezcan a la misma población. Utilizaremos las tablas
de la distribución F de Snedecor (inversa) para
determinar el correspondiente coeficiente crítico. b2/
b2/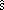 w2
<< 1? Aplicarlo a la resolución del
siguiente
w2
<< 1? Aplicarlo a la resolución del
siguiente| Teorema 3.2: Si para todo i≠k, xi≠xk, entonces p(x) = ∑ i=0 m fi | ∏
j≠i (x-xj) ∏ j≠i (xi-xj) |
| x
k |
1 |
2 |
4 |
5 |
| f
k |
0 |
2 |
12 |
21 |
| f[xi]
= |
fi | para
todo i=0,1...m |
| f[xi,xi+1,xj]
= |
f[xi+1,...xj]
- f[xi,...xj-1] xj - xi |
para
todo i=0,1...m-1,
j=i+1,...m |
| f[x0] f[x1] f[x2] f[x3] |
> f[x0,x1] > f[x1,x2] > f[x2,x3] |
> f[x0,x1,x2] > f[x1,x2,x3] |
> f[x0,x1,x2,x3] |
| k |
0 |
1 |
2 |
3 |
| x
k |
1 |
2 |
4 |
5 |
| f
k |
0 |
2 |
12 |
21 |
| x
k |
1 |
2 |
4 |
5 |
| f(x
k) |
0 |
2 |
12 |
21 |
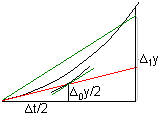
Actividad 3.17.
Teniendo en
cuenta el
| Teorema -3.6:
Para todo fcC r(R→R),
xcC1(R→R),
|
dr f
dtr |
(x(t)) = ﴾dx/dt﴿r |
dr f
dxr |
(x) |
| ε' = C' | dr f dtr |
(ζ) para
algún ζc[0,m], |
| ε = C | dr f dxr |
(ξ) para algún ξc[a,b] con C=hr+1 C' |
 Actividad
3.24.
El método de Euler daría un resultado exacto si la
derivada y',
representada por la pendiente de la curva, fuera constante (y por lo
tanto la segunda
derivada valiera cero). Si no es así, encontraremos
que la derivada
en el punto (t1,y1)
será f(t1,y1)=f(t0+∆t,y0+∆0y)≠f(t0,y0).
En este caso, podemos obtener una mejor aproximación si
calculamos
la derivada en el punto intermedio (t0+∆t/2,y0+∆0y/2)
y tomamos y1=y0+∆1y
con ∆1y=f(t0+∆t/2,y0+∆0y/2)·∆t,
y así sucesivamente (método
de Runge de segundo orden); en este caso el error es
proporcional a (∆t)3 .
Actividad
3.24.
El método de Euler daría un resultado exacto si la
derivada y',
representada por la pendiente de la curva, fuera constante (y por lo
tanto la segunda
derivada valiera cero). Si no es así, encontraremos
que la derivada
en el punto (t1,y1)
será f(t1,y1)=f(t0+∆t,y0+∆0y)≠f(t0,y0).
En este caso, podemos obtener una mejor aproximación si
calculamos
la derivada en el punto intermedio (t0+∆t/2,y0+∆0y/2)
y tomamos y1=y0+∆1y
con ∆1y=f(t0+∆t/2,y0+∆0y/2)·∆t,
y así sucesivamente (método
de Runge de segundo orden); en este caso el error es
proporcional a (∆t)3 .
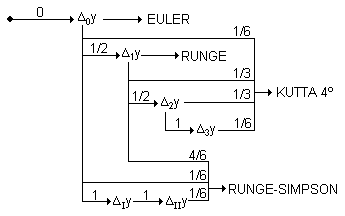
| ty yy |
t0. y0. |
t1
= t0+∆t y1 = ∆0y/6 + ∆1y/3 + ∆2y/3 + ∆3y/6. |
|||
| t y y' ∆0y ∆1y ∆2y ∆3y |
t0. y0. f(t,y) ∆0y |
t0+∆t/2. y0+∆0y/2. f(t,y) ∆1y |
t0+∆t/2. y0+∆1y/2. f(t,y) ∆2y |
t0+∆t y0+∆2y f(t,y) ∆3y |
|
| t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| x |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
| s |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
que expresaría una relación estructural de dependencia de s(t+1) respecto de x(t) y s(t) . |
| t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| x |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
| s |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
| y |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
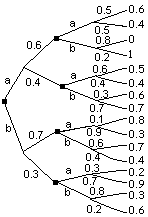
| Actividad
4.11. Un árbol de
decisión consiste en una bifurcación entre varias
decisiones posibles,
a raíz de cada una de las cuáles pueden producirse
distintos eventos
con determinadas probabilidades (o posibilidades), en respuesta a los
cuáles pueden a su vez tomarse distintas decisiones, y
así
sucesivamente, como se indica en las figuras adjuntas. Al final de cada
rama hay que evaluar su probabilidad (o posibilidad) así como
los
resultados obtenidos en relación a los objetivos previamente
definidos,
a fin de determinar una estrategia racional de decisiones sucesivas. Ejercicio 4.9: determinar la estrategia óptima de acuerdo con el árbol de decisión superior adjunto, donde los cuadrados indican bifurcación entre decisiones, se indica la probabilidad de cada evento, y al final de cada rama se indica el correspondiente resultado o probabilidad de satisfacción. Evaluar la expectativa de probabilidad de satisfacción después de cada decisión. Imaginar una posible aplicación de dicho arbol de decisión, o bien elaborar otro árbol de decisión para algún problema. NOTA: recordad que las probabilidades condicionales se multiplican, y las probabilidades de opciones alternativas se suman. |
 |
| BASIC | C | octave/MatLab | |
| matrices | x(3), y(2)(3) | x[3], y[2][3], {3,5,7,9} | x(3), y(2,3), [3,5,7,9], [3;5;7;9], 3:2:9 |
| suma | x+y | x+y | x+y |
| resta | x-2 | x-2 | x-2 |
| producto | x*y | x*y | x*y, x.*y |
| cociente | x/y | x/y | x/y, x./y |
| potencia | 2^3 | pow(2.,3.) | 2^3, 2.^3 |
| raíz cuadrada | SQR(9) | sqrt(9.) | sqrt(9) |
| asignación de un valor | x=3 | x=3; | x=3; x=3 |
| condición de igualdad | x=y | x==y | x==y |
| desigualdades | x>y, y>=2, x<y, x<>y | x>y, y>=2, x<y, x!=y | x>y, y>=2, x<y, x~=y |
| negación | NOT p | !p | ~p |
| conjunción | p AND q | p && q | p & q |
| disyunción | p OR q | p || q | p | q |
| condicional |
if p then
... else ... end if |
if(p) {...} else {...} |
if
p ... else ... end |
| bucle | for
i=0 to 10 step 2 .... next i |
for(i=0;i<=10;i+=2) {...} |
for
i=0:2:10 ... end |
| mostrar un valor | print
"x=";x; print "x=";x |
printf("x=%f",x); printf("x=%f\n",x); |
fprintf('x=%f',x);
x fprintf('x=%f\n',x); x |
| introducir un dato | Input
"x=",x x=InputBox("x=") |
printf("x="); scanf("%f",&x); | x=input('x='); |
 ctividad 5.2.
Antes de redactar un programa en un lenguaje de programación
determinado conviene confeccionar un diagrama de flujos en el que se
indique el
orden de ejecución de las distintas instrucciones. Para ello
cada
instrucción se representa dentro de un rectángulo,
excepto los
condicionales que se representan dentro de un rombo, como se indica en
la figura adjunta, y se indica con flechas el orden de
ejecución. El
inicio del programa se indica con un círculo, y su final con un
rectángulo ovalado. Los bucles aparecerán como un
circuito cerrado con
una condición de salida.
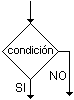
ctividad 5.2.
Antes de redactar un programa en un lenguaje de programación
determinado conviene confeccionar un diagrama de flujos en el que se
indique el
orden de ejecución de las distintas instrucciones. Para ello
cada
instrucción se representa dentro de un rectángulo,
excepto los
condicionales que se representan dentro de un rombo, como se indica en
la figura adjunta, y se indica con flechas el orden de
ejecución. El
inicio del programa se indica con un círculo, y su final con un
rectángulo ovalado. Los bucles aparecerán como un
circuito cerrado con
una condición de salida.| moderadamente el
consumo
energético y (3) reducir
drásticamente el consumo energético, en relación a
los siguientes escenarios: (a) fuentes de energía actualmente
existentes, (b) descubrimiento de una fuente de energía
radicalmente nueva y (c) posibilidad de trasladarse a otro planeta
virgen con abundancia de recursos, suponiendo que las probabilidades de
los escenarios son P(a)=0'6, P(b)=0'3, P(c)=0'1 y que las
probabilidades
condicionales de conseguir el objetivo de que la humanidad viva
satisfactoriamente
vienen dadas por la tabla adjunta. |
|
|||||||||||||||||||||
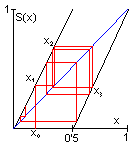
| Ejercicio 6.5:
definimos el operador Shift mediante S(x)=2x si 0≤x<0'5,
S(x)=2x-1 si 0'5≤x<1, según se muestra en la figura adjunta.
En la figura inferior se indica la generación gráfica de
los sucesivos valores de xt.
Si representamos
x en sistema binario (con 0s y 1s), para obtener S(x) deberemos
simplemente desplazar los bits (0s y 1s) un lugar a la izquierda y
descartar la parte entera si aparece. ¿Que valores de x
generarían una sucesión periódica? Comprobar que
el operador Shift cumple las propiedades de: a) Sensibilidad a las condiciones iniciales (para δ=0'01 en sistema binario). b) Densidad de puntos periódicos. c) Mezcla. A tal efecto dividiremos la clase en dos grupos,
|
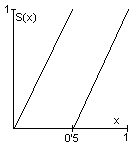  |