Essent f '(m,r) = m + (m-1)/(r-1) el denominador del pes normalitzat per al Sistema de Resta Major, s'acompleix que, per a r³2 i m>1,
Podem expressar també el denominador del pes normalitzat per al Sistema de Resta Major per
Naturalment, si r=2, a(r)=2 , corresponent al sistema de Saint Lagué, mentre que limr®¥ a(r) =1 , corresponent a la Regla d'Hondt. En general serà
Comparació de les condicions de garantia:
Si recordem que el sistema de Resta Major es el que dóna una millor aproximació a la proporcionalitat exacta i que la Regla d'Hondt tendeix a primar a la majoria, podem suposar que el Sistema de Saint Lagué tendisca a primar a les minories: de fet, si més no en sistemes de quocient major, quan major siga el denominador del pes normalitzat, serà menor la proporció que garanteix l'obtenció d'un lloc: el denominador del pes normalitzat, a(m-1)+1 , augmentarà amb el paràmetre a per a tot m>1, al temps que el denominador de la corresponent quota repartidora, a(n+1-r)+r , augmentarà també amb aquest paràmetre... sempre que r<n+1.
Per a Resta Major el corresponent denominador de la quota repartidora val g'(n,r)=n·r/(r-1) . Podem comprovar que aquest valor correspon a la quota repartidora d'un sistema de quocient major amb paràmetre variable a(r)=r/(r-1). En efecte,
Si r=2 valdrà g'(n,2)=2n, coincidint, naturalment, amb el corresponent a Saint Lagué.
Si r=n+1, g'(n,n+1) = n·(n+1)/n = n+1, que coincideix amb el corresponent a la Regla d'Hondt. Però en aquest cas el corresponent a Saint Lagué val també 2(n+1)-r=2(n+1)-(n+1)=n+1.
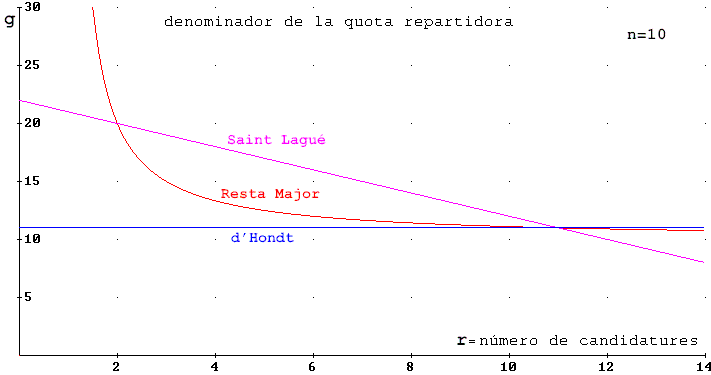
Per a valors intermedis de r la quota repartidora normalitzada amb Resta Major tindrà un valor intermedi entre les de Saint Lagué i Hondt, com es pot veure en la figura:

Observem que per a 2<r<n+1 el denominador amb Saint Lagué és major, i per tant menor la quota repartidora. Això permet obtenir el primer lloc amb un número de vots inferior al de Resta Major, sistema que dóna una millor aproximació a la proporcionalitat exacta, i pot arribar a vulnerar la proporcionalitat estricta.
Suposem per exemple que amb 100 votants per a 10 llocs una candidatura obté 52 vots. Com la seua proporció exacta és 10x52/100=5'2, d'acord amb una proporcionalitat estricta hauria d'obtenir com a mínim 5 llocs. Però si els altres 48 votants atorguen 8 vots en primera posició a cadascú de 6 candidats diferents, cadascú d'aquests obtindrà una puntuació de 8. I com el 5é de l'altra candidatura obté una puntuació de 52/(2x5-1) = 52 / 9 = 5'78, ja no resulta elegit, i la candidatura amb 52 vots obté únicament 4 llocs.
Observem que, amb 7 candidatures, la quota repartidora amb Saint Lagué és 100/(2x11-7)=100/15=6'67, de manera que 8 vots en primera posició garanteixen l'elecció.
Pel contrari, amb el mateixos vots, aplicant la Regla d'Hondt el 6é candidat de la candidatura amb 52 vots tindria una puntuació de 52/6=8'67>8, i resultaria elegit. La candidatura amb 52 vots obtindria així 6 llocs, i els altres 4 s'els haurien de sortejar entre els 6 candidats que havien rebut 8 vots en primera posició.
Observem que la quota repartidora amb la Regla d'Hondt és 100/11=9'09, independentment del número de candidatures, de manera que 8 vots en primera posició no garanteixen l'elecció.
Això respecta la proporcionalitat estricta, però no és la millor aproximació a la proporcionalitat exacta. Aquesta la dóna el sistema de Resta Major: la candidatura amb 52 vots té un cocient enter de 5, corresponent-li un mínim de 5 llocs, i una resta de 0'2; però com a cada candidatura amb 8 vots li correspondria una proporció exacta de 10x8/100=0'8, les seues restes són superiors, i per tant s'haurien de sortejar els 5 llocs restants.
Observem que, amb 7 candidatures, el denominador del pes normalitzat amb Resta Major per al 5é candidat és 5+(5-1)/(7-1)=5+4/6=5'67, i per tant la seua puntuació seria 52/5'67=9'18>8, amb una quota repartidora de 100x6/70=8'57, resultant per tant elegit. Ara bé, el denominador del pes normalitzat per al 6é candidat és 6+(6-1)/(7-1)=6+5/6=6'83, i per tant la seua puntuació seria 52/6'83=7'61<8, no resultant elegit.
Assenyalem, per altra banda, que la "ventaja" que dóna Saint Lagué a les candidatures minoritàries no s'acompleix si r>n+1. Suposem per exemple que els 48 votants restants s'hagueren distribuït no entre 6, sinó entre 24 candidatures, amb 2 vots cadascuna (el 2% del total). En aquest cas, com el 10é candidat de la candidatura amb 52 vots obté una puntuació de 52/(2x10-1)=52/19=2'74>2, resultarà elegit, i la candidatura amb 52 vots coparà els 10 llocs. Amb la Regla d'Hondt passaria el mateix (52/10=5'2>2)
Això no pot passar amb el sistema de Resta Major, per tal com
aquest és un sistema de proporcionalitat forta, i amb una proporció
exacta de 5'2 una candidatura no pot obtenir menys de 5 ni més de
6 llocs. De fet la seua resta de 0'2 és igual a la de les altres
candidatures, 10x2/100=0'2, de manera que els restants 5 llocs s'els haurien
de sortejar entre les 25 candidatures.
Comparació de les condicions de possibilitat:
Observem per altra banda que, encara que la condició de garantia per al sistema de Resta Major corresponga al d'un sistema de quocient major amb paràmetre variable a(r)=r/(r-1), la condició de possibilitat amb aquest sistema de quocient major serà
Per tant, si el número r de candidatures és diferent a 2 i a (n-1)/(m-1) , els sistema de Resta Major no és matemàticament equivalent al sistema de quocient major amb paràmetre variable a(r)=r/(r-1)
Si r=2, el sistema de Resta Major sí es matemàticament equivalent al corresponent sistema de quocient major, coincident amb el de Saint Lagué.
Pel contrari, en cas que el número de candidatures siga r=(n-1)/(m-1) , la condició de possibilitat coincidirà per un valor determinat m=1+(n-1)/r , però no per a la resta. Per tant, els sistemes tampoc seran matemàticament equivalents.
Suposem per exemple que n=4; en aquest cas, com r i m han de ser números naturals, han de valer r=3, m=2. El paràmetre a(r) valdrà per tant a(3)=3/2=1'5 , i el denominador corresponent serà f(m)=1'5m-0'5 .
Suposem ara que per a 4 llocs tenim tres candidatures que obtenen respectivament 23, 14 i 3 vots. Per Resta Major, les seues proporcions exactes seran respectivament 4x23/40=2'3, 4x14/40=1'4 i 4x3/40=0'3. Per tant, correspondran 2 llocs a la primera candidatura i 2 llocs a la segona.
Pel contrari, si apliquem el corresponent sistema de quocient major, tindrem
| m | f(m)=1'5m-0'5 | 23/f(m) | 14/f(m) | 3/f(m) |
| 1 | 1 | 23 | 14 | 3 |
| 2 | 2'5 | 9'2 | 5'6 | |
| 3 | 4 | 5'75 |
Certament, les condicions de possibilitat i de garantia per al segon lloc són les mateixes amb els dos sistemes. De fet, amb 14 de 40 vots i una proporció de 14/40=0'35 s'acompleix la condició de possibilitat (0'35>0'333) per al segon lloc, però no la condició de garantia (0'35<0'417). I s'obté amb el sistema de Resta Major, però no amb el sistema de quocient major corresponent. Pel contrari, amb 23 de 40 vots i una proporció de 23/40=0'575 les condicions de possibilitat per al tercer lloc difereixen amb els dos sistemes: no es donen amb el sistema de Resta Major (0'575<0'583), però sí amb el sistema de quocient major corresponent (0'575>0'533). I s'obté amb el sistema de quocient major corresponent, però no amb el sistema de Resta Major.
Per tant, podem concloure que si hi ha més de dos candidatures
aquests dos sistemes no són equivalents. I caldria precisar que
quan parlem de sistemes de classificació
de paperetes per Resta Major, realment es tracta de sistemes de classificació
de paperetes pel sistema de quocient major corresponent, amb paràmetre
variable a(r)=r/(r-1), amb les mateixes condicions de garantia però
diferents condicions de possibilitat amb més de dues candidatures.
Comparació de les condicions d'obtenció:
En tot cas, en el marge entre la proporció de vots que possibilita l'obtenció d'un lloc i la proporció de vots que la garanteix hi ha una variabilitat que pot determinar també diferents condicions d'obtenció d'un lloc en diferents sistemes electorals.
A tal efecte, examinarem quina candidatura obté un lloc per un sistema de quocient major amb paràmetre a quan el sistema de Resta Major dóna empat. En aquest cas, si dues candidatures obtenen respectivament unes proporcions p1 i p2 de vots, haven n llocs a distribuir, suposarem que
Aleshores, per Resta Major aquestes candidatures tindran garantides respectivament s1 i s2 llocs, i estaran empatades per al lloc següent (el que l'obtinguen directament o no o hagen de desempatar dependrà de les restes de les demés candidatures si hi hi i de quants llocs resten per distribuir). Examinarem per tant el resultat que dóna un sistema de quocient major de paràmetre a per a la seua obtenció, respectivament, del llocs m1=s1+1 i m2=s2+1 . A tal efecte, haurem de comprovar si
Ara bé, m1=s1+1=n·p1-e+1, i igualment m2=n·p2-e+1 . Per tant, aquesta desigualtat és equivalent a
Per tant, si a·e<1 la desigualtat s'acomplirà si p1 > p2, i pel contrari si a·e>1 s'acomplirà si p1 < p2 . En altres paraules: si e<1/a guanya la candidatura majoritària, i si e>1/a guanya la candidatura minoritària. En cas que e=1/a, estaran empatades.
Per tant, en el cas de la Regla d'Hondt (a=1), com sempre e<1, en cas d'empat per Resta Major guanya sempre la candidatura majoritària.
Pel que fa al sistema de Saint Lagué (a=2), si e<0'5 guanya la candidatura majoritària, i si e>0'5 guanya la candidatura minoritària. Observem que en el cas de dues candidatures, r=2, si hi ha empat de restes ha de ser e=0'5, i per tant hi ha empat també amb el sistema de Saint Lagué (que amb dues candidatures és equivalent a Resta Major). I naturalment, per a que puga haver empat de restes amb e>0'5, és necessari que el número de llocs pendents de distribuir per restes (igual a Si=1:r ei )siga major que 2 .
En cas del sistema de quocient major amb paràmetre variable a(r)=r/(r-1), amb r candidatures, si e<(r-1)/r guanyarà la candidatura majoritària, si e>(r-1)/r guanyarà la candidatura minoritària, i si e=(r-1)/r estaran empatades.
Ara bé, suposem que es disputen un número de restes k=Si=1:r ei £ r-1 (per tal com tot ei<1). Aleshores, per a que una candidatura amb resta e>(r-1)/r puga perdre directament el lloc restant caldria que haguera altres k candidatures amb restes iguals o majors que e. Però en aquest cas s'acompliria k ³ (k+1)e > (k+1)(r-1)/r, que és equivalent a k·r>k·e-k+r-1, i per tant a k>r-1, el qual és impossible. Per tant, una candidatura amb resta e>(r-1) mai pot perdre directament el lloc restant: si hi ha 2 candidatures amb empat en la resta e>(r-1)/r, ambdues obtindran un lloc més.
Si e=(r-1)/r, únicament es produirà empat amb el sistema de quocient major amb a(r)=r/(r-1) si es disputen k=r-1 restes i les r candidatures estan empatades.
Per tant, amb aquest sistema una candidatura minoritària amb resta empatada mai obté directament el lloc en disputa, i únicament podria empatar amb totes les demés candidatures alhora. Així doncs, encara que les condicions de garantia són les mateixes que amb el sistema de Resta Major, les condicions d'obtenció d'un lloc beneficien a la majoria, encara que no tant com amb la Regla d'Hondt.