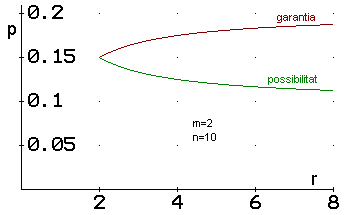
Figura 1
Garantia i possibilitat amb el sistema de Resta Major
en funció del número de candidatures
Garantia d'obtenir representació:
Si es presenten un total de r candidatures, una candidatura té la garantia d'obtenir com a mínim m de n llocs si la seua proporció de vots supera a la que donaria un empat entre les r candidatures per als darrers r-1 llocs, si per a aquesta és indiferent la forma com es distribuisquen els llocs entre les demés candidatures (condició d'indiferència) i els llocs s'assignen cadascú per separat en funció del número de vots a cada candidatura.
En efecte, en tal cas necessàriament alguna de les altres candidatures tindrà una proporció de vots inferior a la de l'empat, que manera que restarien r-1 candidatures per a distribuir-se els r-1 llocs.
Naturalment, allò que importa és
la proporció entre el total dels vots vàlids a
candidatures,
sense tenir en compte els vots nuls o en blanc.
Possibilitat d'obtenir representació:
Si es presenten un total de r candidatures, una candidatura té la possibilitat d'obtenir com a mínim m de n llocs si la seua proporció de vots no és inferior a la que donaria un empat entre les r candidatures per al darrer lloc, si per a aquesta és indiferent la forma com es distribuisquen els llocs entre les demés candidatures (condició d'indiferència).
En efecte, si fora inferior necessariament alguna de les altres candidatures tindria una proporció de vots superior a la de l'empat, de manera que tindria precedència per al darrer lloc. I per altra banda, en cas d'empat la possibilitat d'obtenir el darrer lloc dependrà de la manera de resoldre-ho.
Naturalment, si hi ha únicament 2
candidatures,
la condició de garantia i la de possibilitat és la
mateixa
llevat del cas d'empat, per tal com r-1=1 .
Els raonaments anteriors no són directament aplicables en sistemes en llista oberta en que no hi ha pròpiament candidatures globals, sinò candidats o candidates individuals. Ni tampoc en sistemes majoritaris, purs o corregits, en que els llocs s'elegeixen en blocs i no cadascú per separat. En aquest darrer cas, pot aplicar-se el raonament als blocs i no als llocs per separat.
Suposem per exemple que tenim un sistema majoritari corregit en el qual cada candidatura inclou 3 noms ordenats per a elegir 5 llocs. En aquest cas hi ha dos blocs: els primers 3 llocs per a la primera majoria, i els darrers 2 llocs per a la segona majoria. Aleshores, si hi ha 3 candidatures que obtenen el mateix número de vots, empataran per als dos blocs. De manera que si alguna de les 3 candidatures obtinguera més de la tercera part dels vots, tindria la garantia d'obtenir con a mínim el segon bloc. Per altra banda, com en el cas de triple empat aquest es produeix també per al primer bloc, obtenir més de la tercera part donaria també la possibilitat d'obtenir el primer bloc. Per exemple, si una candidatura obté 21 de 60 vots té la garantia d'obtenir si més no els darrers 2 llocs (si, per exemple, les altres dos candidatures obtenen 22 i 17 vots, respectivament), però també podria obtenir els primers 3 llocs (si, per exemple, obtenen 20 i 19 vots, respectivament).
En tot cas, en allò que segueix estudiarem sistemes
electorals
no majoritaris amb candidatures tancades. El resultat d'aquest estudi
es
podrà aplicar per al disseny de sistemes electorals
proporcionals
en llista oberta.
D'acord amb aquest sistema, si hi ha r candidatures i cada candidatura i obté una proporció de pi vots per a n llocs, se l'assigna inicialment la part entera si de pi·n, i es calcula la resta
La condició que garanteix que una candidatura obtinga per Resta Major m de n llocs és que obtinga una proporció de vots
Si escrivim el segon termini de la primera desigualtat com
Per altra banda, la condició que possibilita que una candidatura obtinga per Resta Major m de n llocs és que obtinga una proporció de vots
L'interval entre la proporció de possibilitat i la de
garantia
és un àmbit d'incertesa, per tal com l'obtenció o
no dels m llocs depen de la manera com es distribuisquen els
vots
restants entre les demés candidatures.
En aquest cas, en efecte, si la candidatura A obté una proporció de vots de 0.2, la candidatura B una proporció de 0.47 i la candidatura C una proporció de 0'33 vots, en el cas de n=7 llocs al multiplicar aquestes proporcions per 7 s'obté 1.40, 3.29 i 2.31 respectivament, i per tant la candidatura A obté 2 llocs, per tal com la seua resta, 0.40, és major que les altres. Tanmateix, en el cas de n=8 llocs, al multiplicar les proporcions per 8 s'obté 1.60, 3.76 i 2.64 respectivament, de manera que la candidatura A solament obté 1 lloc, per tal com la seua resta, 0.60, és inferior a les altres.
Per això, el sistema descrit de Resta Major no és
adequat
per a utilitzar-ho directament per a ordenar candidatures si aquestes
són
més de 2 (com hem assenyalat, en el cas de 2 candidatures les
proporcions
de garantia i possibilitat coincideixen, i per tant no hi ha franja
d'incertesa),
encara que aquesta ordenació és possible de forma
unívoca
utilitzant un algoritme adequat. Tanmateix,
com la corresponent proporció de garantia sí disminueix
uniformement
amb el número n de llocs, sí pot utilitzar-se com
a referència per a ordenar candidatures
en
llista oberta.
Direm que un sistema electoral és proporcional en sentit feble quan, en cas que totes les candidatures hagen obtés una proporció de vots que corresponga a un número exacte de representants (és a dir, que pi·n siga un número enter per a tot i=1:r), aquest és el que obtenen (és a dir, mi=pi·n).
Direm que un sistema electoral és proporcional en sentit estricte o simplement proporcional quan cada candidatura obté com a mínim un número de representants que difereix en menys de la unitat de la part proporcional exacta corresponent a la seua proporció de vots (és a dir, p·n-1<m). Això s'acomplirà si i solament si la proporció de vots que garanteix m llocs és inferior o igual a m/n . En efecte, en altre cas podria donar-se que, essent m' un número enter igual o inferior a p·n, obtingués un número de llocs m<m', amb el qual m≤p·n-1 .
Direm que un sisteme electoral és proporcional en sentit fort quan el número de representants que obté cada candidatura difereix en menys de la unitat de la part proporcional exacta corresponent a la seua proporció de vots (és a dir, p·n-1<m<p·n+1). Això s'acomplirà si i solament si la proporció de vots que garanteix m llocs és inferior o igual a m/n i la proporció de vots que possibilita m llocs és superior a (m-1)/n .
Naturalment, tot sistema electoral proporcional en sentit fort ho és en sentit estricte. I tambó ho és en sentit feble: si la proporció exacta correspon a un número enter i s'obtingués un número diferent de representants, la diferència seria com a mínim d'una unitat.
La proporcionalitat estricta també implica proporcionalitat feble: si a totes les candidatures les correspon com a proporció exacta un número enter i alguna tingués un número superior de representants, altra hauria de tenir un número inferior, com a mínim d'una unitat menys que la proporció exacta.
Per altra banda, si un sistema electoral és proporcional en sentit feble i hi ha únicament 2 candidatures, per a aquestes s'acompliran també les condicions de proporcionalitat forta: en efecte, si per a una candidatura la proporció de vots és p=m/n, per a l'altra serà p'=(n-m)/n, i per tant, al correspondre en els dos casos la proporció exacta a uns números enters de representants (m i n-m, respectivament), aquestos seran els que obtindran; per tant, la proporció de garantia per a m llocs ha de ser inferior a m/n i per tant a (m+1)/n; però si la proporció de vots fora p=(m-1)/n, obtindria m-1 i no m representants, i per tant la proporció de possibilitat para m llocs ha de ser superior a (m-1)/n , acomplint-se per tant les dos condicions de proporcionalitat forta.
Per tant, la distinció entre proporcionalitat forta, estricta i feble s'aplica únicament als casos de més de 2 candidatures.
És immediat que el sistema de Resta Major és proporcional en sentit feble: si pi·n és un número enter per a tota candidatura i=1:r, aleshores totes les restes valdran zero i per a totes les candidatures
Podem comprobar que el sistema de Resta Major és també proporcional en sentit fort: la proporció de vots que garanteix m llocs és
Per altra banda, podem mesurar el grau de
proporcionalitat d'un sistema electoral per la distància
global entre les proporcions exactes que correspondrien al conjunt de
candidatures
i la distribució de lloc entre elles.
Sistemes electorals de quocient major:
Ara bé, com hem assenyalat el sistema de Resta Major no és adequat per a utilitzar-ho directament per a ordenar candidatures si aquestes són més de 2. Per a aquesta ordenació es poden utilitzar sistemes de quocient major.
Un sistema electoral de quocient major es basa en una sèrie de divisors f(m) per a cada posició m en una candidatura, tal que f(m) és positiu i monòton creixent si m≥1, de manera que al candidat que ocupa la posició m en una candidatura que obté una proporció p de vots se li assigna una puntuació igual al quocient p/f(m) , i es van atorgant successivament els llocs als candidats que tenen major quocient fins a esgotar els n llocs a distribuir.
Per tal com el sistema electoral és equivalent si es multipliquen tots els divisors per un número constants positiu, podem imposar, sense pérdua de generalitat, que f(1)=1 .
Per a obtenir la proporció de vots la superació de la qual garanteix l'obtenció de m de n llocs per una candidatura, haurem d'analitzar la situació en la qual es produeix un empat entre r candidatures per als darrers r-1 llocs. En aquest cas, si totes les candidatures i=1:r obtingueren el lloc mi per al qual estan empatades s'haurien atribuït un lloc més dels existents, és a dir,
Aquest valor de l determinarà la proporció
Aleshores, si f(m) és una funció contínua per a tot m≥0, aquesta relació s'haurà d'acomplir també si, per tot i=1:r-1, mi=0 . Aleshores, prenent mr=m , s'acomplirà
En aquest cas, efectivament,
Per la seua banda, per a obtenir la proporció de vots que dóna possibilitat d'obtenció de m de n llocs per una candidatura, haurem d'analitzar la situació en la qual es produeix un empat entre r candidatures per al darrer lloc. En aquest cas, si totes les candidatures i=1:r obtingueren el lloc mi per al qual estan empatades s'haurien atribuït r-1 llocs més dels existents, és a dir,
Naturalment, si el número de candidatures és r=2, la condició de possibilitat coincideix amb la condició de garantia
Per a que un sistema de quocient major siga proporcional en sentit feble, s'hauria d'acomplir que si per a tota candidatura i=1:r el producte mi=n·pi és un número enter aleshores cada candidatura i obté exactament n·pi llocs i per tant s'hauria d'acomplir que, per a tot parell de candidatures i,j=1:r, si pi>0
Per altra banda, si el número r de candidatures no està limitat, la proporció de vots que dóna possibilitat d'obtenir m de n llocs es pot fer tan petita con es vulga incrementant r, i per tant els sistemes de quocient major que estem estudiant no seran proporcionals en sentit fort.
Per a determinar si són proporcionals en sentit estricte haurem d'analitzar si la proporció a partir de la qual estan garantits m de n llocs és inferior a (m+1)/n.
Amb a≥1, aquesta proporció,
Si a=1, la inequació es redueix a
Si a>1, hem d'examinar el discriminant de la corresponent equació de segon grau en m, que és igual a
Tanmateix, per a cada sistema electoral de quocient major definit pels divisors f(m)=a·m+1-a amb a>1 podem trobar intervals de valors de n per als quals sí estiga garantida la proporcionalitat estricta. Aquests intervals estaran formats pels valors de n compresos entre dos arrels reals de l'equació
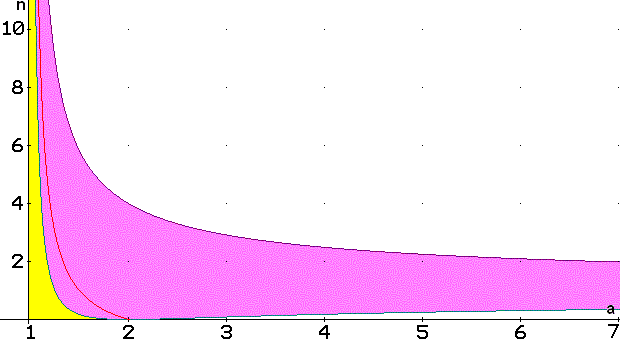
Ara bé, per les propietats de les equacions de segon grau, la condició de proporcionalitat estricta solament deixarà d'acomplir-se per a valors de m enters positius compresos entre les dos eventuals arrels de la corresponent equació de segon grau en m . Però, per a n>0 i a>1, el termini independent d'aquesta equació és
Per altra banda, les dos arrels que limiten l'interval sombrejat en lila tendeixen a 1 quan el paràmetre a tendeix a infinit, de manera que per a n=1 està garantida la proporcionalitat estricta per a qualsevol valor de a major o igual que la unitat.
Així doncs, per a cada valor de a podrem acotar inferiorment els valors de n per als quals es pot vulnerar la proporcionalitat estricta. Per exemple, si a=1.5 això podria passar únicament a partir de n=6, i si a=2 podria passar únicament a partir de n=4 .
Per altra banda, per a determinar el número de candidatures necessàries per a la vulneració de la proporcionalitat estricta caldrà estudiar la possibilitat d'acompliment de la desigualtat
Si a>1, aquesta condició de vulneració de la proporcionalitat s'acomplirà quan
Aquests arrels es poden obtenir gràficament per la intersecció entre l'hipèrbola en funció de m corresponent a l'expressió de la dreta de la condició de vulneració de la proporcionalitat i la recta en funció de m corresponent a l'expressió de la dreta de la desigualtat
Ara bé, es pot veure que l'expressió de la dreta de la condició de vulneració de la proporcionalitat que ens dóna la cota inferior del número r de candidatures que permet aquesta vulneració augmenta amb el número n de llocs i disminueix amb el número m de representants de la candidatura. Per tant, per a cada sistema de quocient major amb paràmetre a i cada número n de llocs a elegir podrem acotar inferiorment el número r de candidatures que permet vulnerar la proporcionalitat estricta, prenent el major valor enter de m que possibilita aquesta vulneració amb n llocs.
Podriem ara estudiar, per a cada sistema de quocient major amb paràmetre a, el mínim valor del número r de candidatures que permet vulnerar la proporcionalitat amb el mínim numero n de llocs tal com es mostrava en la Figura 3. Ara bé, la cota inferior del número r de candidatures que permet vulnerar la proporcionalitat depen estrictament del quocient
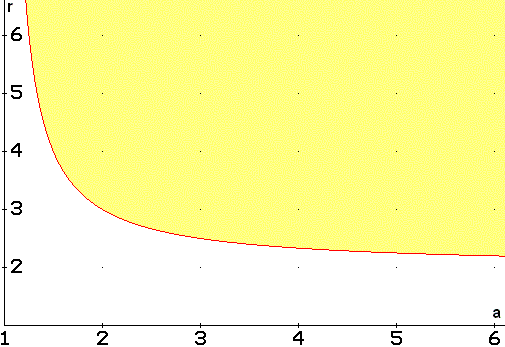
Figura 5
Valors globals del número r de
candidatures
que permeten la vulneració de la proporcionalitat.
Anem a veure ara dos casos particulars de sistemes electorals de
quocient
major:
És el sistema electoral de quocient major amb a=1, és a dir, amb denominador f(m)=m.
En aquest cas, la condició de garantia d'obtenir m de n llocs és
Per la seua banda, la condició de possibilitat d'obtenir m de n llocs amb r candidatures és
Si r=2, l'expressió de la dreta de les condicions de possibilitat i garantia coincideixen.
Per la seua banda, i com ja hem assenyalat, la Regla d'Hondt és un sistema de proporcionalitat estricta: la condició corresponent no pot vulnerar-se.
Ara bé, la Regla d'Hondt, com tots els sistemes de quocient
major,
no és un sistema de proporiconalitat forta. I el seu grau
de proporcionalitat és inferior al del sistema de Resta
Major.
És el sistema de quocient major amb a=2, és a dir, amb denominador f(m)=2m-1
La seua condició de garantia d'obtenir m de n llocs amb r candidatures és
Per la seua banda, la condició de possibilitat d'obtenir m de n llocs amb r candidatures és
Cal assenyalar que en el cas de dos candidatures, r=2, les condicions de garantia i possibilitat són, respectivament,
La condició de proporcionalitat estricta amb el Sistema de Saint Lagué és
Per exemple, si n=4, la proporcionalitat estricta es pot vulnerar amb m=2 i 4 o més candidatures. I si n=3, la condició de proporcionalitat estricta es pot vulnerar amb m=2 i 5 o més candidatures, o amb m=3 i 4 o més candidatures.
Per això, el sistema de Saint Lagué no és
adequat
per a distribuir llocs. Ara bé, el sistema de Saint Lagué
sí es pot utilitzar per a ordenar llocs, per tal com les
estratègies
de dispersió controlada de vots únicament
poden guanyar llocs en la cua a costa de perdre-l`s en la
capçalera.