2.2 Ecuaciones de la Dinámica de Fluidos Perfectos

Ecuación de Continuidad :

$\begin{displaymath} \frac{\partial \rho}{\partial t} + \vec{\nabla} . (\rho \... ..._{V} \rho dV = \int \int_{\Sigma} \rho \vec{v} d \vec{\Sigma} \end{displaymath}$ (1)

$\Longrightarrow$ Conservación de la masa
$\Longrightarrow$ Flujo incompresible $\Longleftrightarrow$ $\vec{\nabla} . \vec{v} = 0$ $\Longleftrightarrow$ $d\rho/dt = 0$
Ecuación de Euler:

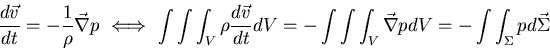$\begin{displaymath} \frac{d \vec{v}}{dt} = - \frac{1}{\rho} \vec{\nabla} p \... ...{V} \vec{\nabla} p dV = - \int \int_{\Sigma} p d \vec{\Sigma} \end{displaymath}$ (2)

$\Longrightarrow$ $- \vec{\nabla} p dV$ es la fuerza que ejerce el fluido que rodea cada elemento de volumen sobre dicho elemento de volumen
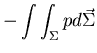$\Longrightarrow$ $\displaystyle{ - \int \int_{\Sigma} p d \vec{\Sigma} }$ es la fuerza total que ejerce el fluido sobre el volumen V
$\Longrightarrow$ Ecuación del movimiento (de un elemento de volumen del fluido)

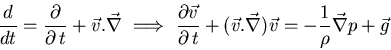$\begin{displaymath} \frac{d }{dt} = \frac{\partial }{\partial t} + \vec{v} . ... ...nabla}) \vec {v} = - \frac{1}{\rho} \vec{\nabla} p + \vec{g} \end{displaymath}$ (3)

$\Longrightarrow$ siendo $\vec{g}=(1/\rho)\vec{f}$ un campo de fuerzas (por unidad de masa) exterior.
$\Longrightarrow$ Campo gravitatorio: $\vec{g} = - \vec{\nabla} \Phi$ con $\Phi$ solución de la ecuación de Poisson.
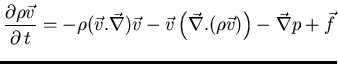
Ecuación de continuidad $\Longrightarrow$ $\displaystyle{\frac{\partial \rho \vec{v} }{\partial t}} = - \rho (\vec{v} ... ...vec{v} \left(\vec{\nabla} . (\rho \vec {v}) \right) - \vec{\nabla} p + \vec{f}$
i) Multiplicando escalarmente por un vector fijo $\vec{e}$ , ii) integrando en el volumen , y iii) aplicando el teorema de la divergencia:

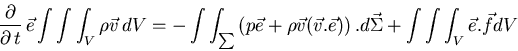$\begin{displaymath} \frac{\partial}{\partial t} \vec{e} \int \int \int_V \... ...ight) . d \vec{\Sigma} + \int \int \int_V \vec{e} . \vec{f} dV \end{displaymath}$ (4)

La cantidad $p \vec{e} + \rho \vec{v} (\vec{v} . \vec{e})$ es el flujo, a través de la frontera, $\sum = \partial V$ , de la componente de la densidad de momento en la dirección $\vec{e}$
Ecuación de la energía:
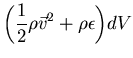Sean $\displaystyle{\left(\frac{1}{2} \rho \vec{v}^2 + \rho \epsilon \right)} dV$ las contribuciones a la energia cinética e interna de un elemento de volumen del fluido ( $\epsilon$ = energia interna específica).

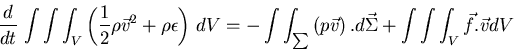$\begin{displaymath} \frac{d}{dt} \int \int \int_V \left(\frac{1}{2} \rho \ve... ...ight) . d \vec{\Sigma} + \int \int \int_V \vec{f} . \vec{v} dV \end{displaymath}$ (5)

i) Desarrollando la derivada total, ii) aplicando el teorema de la divergencia en la integral de supericie, y iii) agrupando términos bajo la divergencia $\Longrightarrow$ La igualdad anterior debe verificarse para todo volumen:

$\begin{displaymath} \frac{\partial }{\partial t} \left(\frac{1}{2} \rho \vec{... ...o \epsilon + p\right) \vec{v} \right] = \rho \vec{g} . \vec{v} \end{displaymath}$ (6)

La cantidad 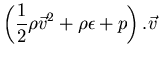$\displaystyle{\left(\frac{1}{2} \rho \vec{v}^2 + \rho \epsilon + p\right) . \vec{v} }$ es el flujo de energía a través de la frontera.
Las ecuaciones de la dinámica de fluidos ideales como un
sistema hiperbólico de leyes de conservación:

$\fbox{\parbox[c]{6.cm}{ \begin{displaymath} \frac{\partial {\bf u}}{\partial ... ...ial {\bf f}^{i}({\bf u})}{\partial x^{i}} = {\bf s}({\bf u}) \end{displaymath}}}$

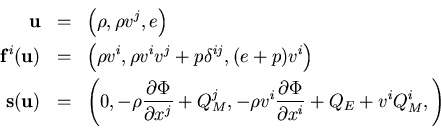
$\begin{eqnarray*} {\bf u} & = & \left( \rho , \rho v^j, e \right) \nonumber \\ ... ...{\partial x^{i}} } + Q_E + v^{i} Q^{i}_M, \right) \nonumber \\ \end{eqnarray*}$

donde u es el vector de variables conservadas, ${\bf f}^{i}({\bf u})$ son los flujos en cada dirección , s(u) son las fuentes, y $Q^{i}_M, Q_E$ son los términos fuentes en las ecuaciones, respectivamente, de la densidad de momento y de energía, debidos al acoplamiento materia-radiación (en el supuesto de considerar fenómenos de transporte). Una ecuación de estado $p = p(\rho,\epsilon)$ cierra el sistema.
Flujo isoentrópico: $\Longrightarrow$ La entropía se conserva en espacio y tiempo
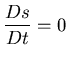$\Longrightarrow$ $\displaystyle{\frac{Ds}{Dt} = 0}$ , $\displaystyle{\frac{D}{Dt} \equiv \frac{\partial}{\partial t} + \vec{v} . \vec{\nabla}}$
Flujo adiabático: $\vec{v} . \vec{\nabla} s = 0$ $\Longrightarrow$ La entropía se conserva a lo largo de las trayectorias $\Longleftarrow$ Ecuación de la energía (fluido perfecto) y estacionario
Fluido perfecto, estacionario, en un campo de fuerzas externo conservativo, $\vec{g}$
$\Longrightarrow$ $\vec{g} = - \vec{\nabla} \Phi$
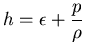$\Longrightarrow$ $h = \displaystyle{\epsilon + \frac{p}{\rho}}$ es la entalpía específica

$\fbox{\parbox[b]{12cm}{ \begin{center}{\bf Teorema de Bernouilli:} $\cal B$... ...isplaystyle{\frac{1}{2} \vec{v}^{2} + \Phi + h } = cte.$\end{center}}}$

$\Longrightarrow$ $\cal B$ es constante a lo largo de las trayectorias
$\Longrightarrow$ Flujo isoentrópico: $\vec{\nabla}$ $\cal B$ $= \vec{v} \times \vec{\omega}$ , $\vec{\omega} = \vec{\nabla} \times \vec{v}$
$\Longrightarrow$ $\cal B$ constante a lo largo de las trayectorias
$\Longrightarrow$ $\cal B$ constante a lo largo de las líneas de vorticidad
$\Longrightarrow$ $\cal B$ constante en espacio (si el flujo es irrotacional)
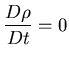Flujo incompresible: $\Longrightarrow$ $\displaystyle{\frac{D\rho}{Dt} = 0}$ , $\Longleftrightarrow$ $\vec{\nabla} . \vec{v} = 0$
$\Longrightarrow$ Si $\rho (t=0, \vec{r}) = cte$ $\rightarrow$ $\rho (t, \vec{r}) = cte \forall t , \forall \vec{r}$
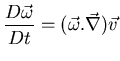
$\Longrightarrow$ $\displaystyle{\frac{D\vec{\omega}}{Dt} = (\vec{\omega} . \vec{\nabla}) \vec{v}}$ $\Longrightarrow$
El flujo de un fluido perfecto incompresible e irrotacional permanece irrotacional $\rightarrow$ Flujo potencial

$\fbox{\parbox[b]{10cm}{ \bf Flujo Potencial: \begin{displaymath} \vec{v} = \vec{... ...nd{displaymath}\begin{displaymath} \Delta \phi = 0 \nonumber \end{displaymath}}}$
Equilibrio Hidrostático
$\vec{v} = 0$ & estacionario $\Longrightarrow$

$\begin{displaymath} - \frac{1}{\rho} \vec{\nabla} p + \vec{g} = 0 \end{displaymath}$ (7)

$\Longrightarrow$ Campo gravitatorio: $\vec{g} = - \vec{\nabla} \Phi$ , con $\Phi$ solución de la ecuación de Poisson: $\Delta \Phi = 4 \pi G \rho$

$\Updownarrow$

Aplicando el operador divergencia a ambos lados de (7)

$\fbox{\parbox[b]{3.95in}{ {\bf Ecuaci\'on de Equilibrio Hidrost\'atico:} \begin{... ...left(\frac{1}{\rho} \vec{\nabla} p \right)} = - 4 \pi G \rho \end{displaymath}}}$

$\Longrightarrow$ Simetría esférica (coordenadas esféricas):

$\fbox{\parbox[b]{4.95in}{ \begin{displaymath} \displaystyle{\frac{1}{r^2} \frac... ...eft(\frac{r^2}{\rho} \frac{dp}{dr} \right)} = - 4 \pi G \rho \end{displaymath}}}$

$\Longrightarrow$ Integrando una vez (en la variable ) y dado que:

$\begin{displaymath} m(r) = \displaystyle{\int_0^r 4 \pi r^2 \rho dr} \Longl... ...ghtarrow \displaystyle{\frac{dm}{dr} = 4 \pi r^2 \rho } \end{displaymath}$ (8)

$\fbox{\parbox[b]{10cm}{ \begin{displaymath} \displaystyle{\frac{dp}{dr} = - G \... ...r^2 \rho } \end{displaymath}\begin{displaymath} p = p(\rho) \end{displaymath}}}$

$\Longrightarrow$ Condiciones de contorno:
A) Centro : $\Longrightarrow$ Superficie: $p(R) = p_{sup}$
B) Mixtas : $m(0)=0, m_{sup} = M$ $\Longrightarrow$ Variable independiente $r \rightarrow m$

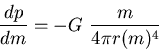$\begin{displaymath} \displaystyle{\frac{dp}{dm} = - G \frac{m}{4 \pi r(m)^4}} \end{displaymath}$ (9)

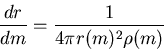$\begin{displaymath} \displaystyle{\frac{dr}{dm} = \frac{1}{ 4 \pi r(m)^2 \rho(m)} } \end{displaymath}$ (10)

$\Longrightarrow$ Versión relativista (TOV):

$\begin{displaymath} { \displaystyle{\frac{dp}{dr} = - G \frac{m(r) \rho(... ...\pi r^3 p }{m} \right] \left[1-\frac{2m}{r}\right]^{-1} }} \end{displaymath}$ (11)

$\Longrightarrow$ Energía Gravitacional:

$\fbox{\parbox[b]{3.95in}{ \begin{displaymath} \Omega = - G \displaystyle{\int_0^M \frac{m(r)}{r} dm} \end{displaymath}}}$
Teorema del Virial
Ecuación de Euler (descripción lagrangiana):

$\begin{displaymath} \frac{d \vec{v}}{dt} = - \frac{1}{\rho} \vec{\nabla} p + \ve... ... \vec{r}}{dt^{2}} = - \frac{1}{\rho} \vec{\nabla} p + \vec{g} \end{displaymath}$ (12)

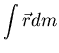
Aplicamos el operador: $\displaystyle{\int \vec{r} dm}$

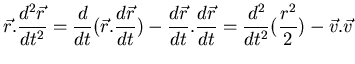$\displaystyle \Longrightarrow$ $\displaystyle \vec{r} . \frac{d^{2} \vec{r}}{d t^{2}} = \frac{d}{dt} (\vec{r}. ... ...ac{d \vec{r}}{dt} = \frac{d^{2}}{dt^{2}} (\frac{r^{2}}{2} ) - \vec{v} . \vec{v}$

$\displaystyle \Longrightarrow$ $\displaystyle \int dm \left( \vec{r} . \frac{d^{2} \vec{r}}{d t^{2}} \right) = \frac{1}{2} \frac{d^{2} I}{dt^{2}} - 2 T$

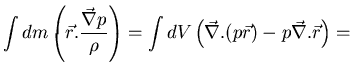$\displaystyle \Longrightarrow$ $\displaystyle \int dm \left( \vec{r} . \frac{\vec{\nabla} p}{\rho} \right) = \int dV \left(\vec{\nabla} . (p \vec{r}) - {p} \vec{\nabla} . \vec{r} \right) =$

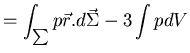$\displaystyle = \int_{\sum} p \vec{r} . d \vec{\Sigma} - 3 \int p dV$

$\fbox{\parbox[b]{12cm}{ \begin{displaymath} \frac{1}{2} \frac{d^{2} I}{d t^{2}} ... ...\sum} p \vec{r} . d \vec{\Sigma} + \int \vec{r} . \vec{g} dm \end{displaymath}}}$

$\begin{displaymath} \vec{g} = - \vec{\nabla} \Phi \Longrightarrow \int \vec{r} . \vec{g} dm = \Omega \end{displaymath}$ (13)

i) Estático, ii) $p_{sup} = 0$ $\Longrightarrow$

$\fbox{\parbox[b]{6cm}{ \begin{displaymath} 3 (\gamma - 1) U + \Omega = 0 \end{displaymath}}}$
Colapso gravitatorio
I. Polvo: p= 0 $\Longrightarrow$

$\begin{displaymath} \frac{d^{2} r}{dt^{2}} = - \frac{G m(r)}{r^{2}} \end{displaymath}$ (14)

$\Longrightarrow$ $t=0, r=r_0 , v=0, \rho = \rho_0$ (constante en ) $\rightarrow$
$\rightarrow$ $m (r_0) = (4/3) \pi r_0^{3} \rho_0$ (constante en )
Dado que:

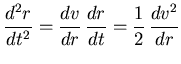$\displaystyle \frac{d^{2} r}{dt^{2}} = \frac{d v}{dr} \frac{d r}{dt} = \frac{1}{2} \frac{dv^{2}}{dr}$

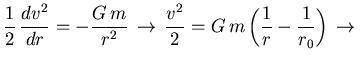$\displaystyle \Longrightarrow$ $\displaystyle \frac{1}{2} \frac{dv^{2}}{dr} = - \frac{G m}{r^{2}} \righta... ...c{v^{2}}{2} = G m \left(\frac{1}{r} - \frac{1}{r_0} \right) \rightarrow$

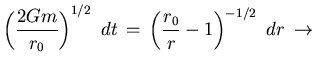$\displaystyle \rightarrow$ $\displaystyle \left(\frac{2Gm}{r_0}\right)^{1/2} dt = \left(\frac{r_0}{r} - 1 \right)^{-1/2} dr \rightarrow$

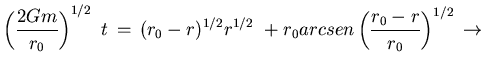$\displaystyle \rightarrow$ $\displaystyle \left(\frac{2Gm}{r_0}\right)^{1/2} t = (r_0 - r)^{1/2}... .../2} + r_0 arcsen \left(\frac{r_0 - r}{r_0} \right)^{1/2} \rightarrow$

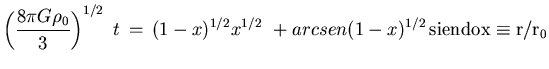$\displaystyle \rightarrow$ $\displaystyle \left(\frac{8 \pi G \rho_0}{3}\right)^{1/2} t = (1 - x)^{1/2} x^{1/2} + arcsen(1 - x)^{1/2} \rm {siendo} x\equiv r/r_0$

Tiempo característico hidrodinámico, $\tau_{\rho}$ $\Longrightarrow$ Haciendo en la expresión anterior:

$\fbox{\parbox[b]{7cm}{ \begin{displaymath} \tau_{\rho} = \left(\frac{3 \pi}{32 G \rho_0}\right)^{1/2} \end{displaymath}}}$

Para el Sol, haciendo $\rho_0 \approx <\rho>_{\odot}$ $\rightarrow$ $\tau_{\rho} \approx 1 hora$

II. Colapso homólogo de polítropos: $p = k\rho^{\gamma}$

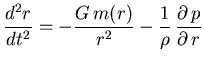$\displaystyle \Longrightarrow$ $\displaystyle \frac{d^{2} r}{dt^{2}} = - \frac{G m(r)}{r^{2}} - \frac{1}{\rho} \frac{\partial p}{\partial r}$

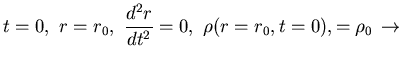$\displaystyle \Longrightarrow$ $\displaystyle t=0, r=r_0 , \displaystyle{\frac{d^{2} r}{dt^{2}}} = 0, \rho (r=r_0, t=0), = \rho_0 \rightarrow$

$\displaystyle \rightarrow$ $\displaystyle p (t=0) = k\rho_0^{\gamma} \equiv p_0$

$\Longrightarrow$ Homólogo: $\rho (t) = \rho_0 (r_0/r)^{3}$ $\Longrightarrow$ $p = p_0 (r_0/r)^{3\gamma}$

$\begin{displaymath} \frac{1}{\rho} \frac{\partial p}{\partial r} = \left... ...c{r_0}{r} \right)^{3 \gamma - 4} \left(\frac{1}{r^{2}} \right) \end{displaymath}$ (15)

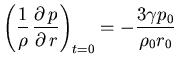
En es: $\displaystyle{\left(\frac{1}{\rho} \frac{\partial p}{\partial r}\right)_{t=0} = - \frac{3 \gamma p_0}{\rho_0 r_0}}$
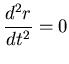
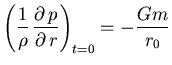
En es: $\displaystyle{\frac{d^{2} r}{dt^{2}}} = 0$ $\rightarrow$ $\displaystyle{ \left(\frac{1}{\rho} \frac{\partial p}{\partial r}\right)_{t=0} = - \frac{G m}{r_0} }$
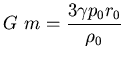
De las dos anteriores expresiones $\Longrightarrow$ $\displaystyle{ G m = \frac{3 \gamma p_0 r_0}{\rho_0} }$
$\rightarrow$ es constante en
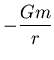
Sustituyendo en (15) y sacando factor común el término $\displaystyle{ - \frac{G m}{r} }$

$\fbox{\parbox[b]{4.5in}{ \begin{displaymath} \displaystyle{ \frac{d^{2} r}{dt^{2... ...left( 1 - \left(\frac{r_0}{r}\right)^{3 \gamma - 4}\right) } \end{displaymath}}}$

$\Longrightarrow$ Valor crítico de $\gamma: \gamma_c = 4/3$

III. Masa de Jeans:

$\begin{displaymath} \frac{\partial \rho}{\partial t} + \vec{\nabla} . (\rho \vec {v}) = 0 \end{displaymath}$ (16)

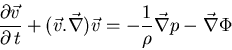$\begin{displaymath} \frac{\partial \vec{v} }{\partial t} + (\vec{v} . \vec{\n... ...vec {v} = - \frac{1}{\rho} \vec{\nabla} p - \vec{\nabla} \Phi \end{displaymath}$ (17)

$\begin{displaymath} \Delta \Phi = 4 \pi G \rho \end{displaymath}$ (18)

$\Longrightarrow$ Linealizando: ${\cal Q} = {\cal Q}_0 + \lambda {\cal Q}_1$ (para: $\cal Q$ = $\rho, p, \vec{v}, \Phi$ )
$\Longrightarrow$ Suponiendo: $\rho_0 = cte.$ , $\vec{v}_0 = 0$
$\Longrightarrow$ Eliminando $\vec v$ y $\Phi$

$\fbox{\parbox[b]{4.5in}{ \begin{displaymath} \displaystyle{ \left(\Delta - \frac... ...+ \frac{4 \pi G \rho_0}{c_s^{2}}\right) \rho_1 = 0 } \end{displaymath}}}$

$\Longrightarrow$ $c_s^{2} = p_1/\rho_1$ es el cuadrado de la velocidad local del sonido ( $c_s^{2} \sim T$ , para gas ideal).
$\Longrightarrow$ Ensayando una solución tipo ondas planas:

$\begin{displaymath} \rho_1 = A exp \{ i (\vec{k} \vec{r}-\omega t)\} \end{displaymath}$ (19)

se obtiene la relación de dispersión: $\omega^{2} = k^{2} c_s^{2} - 4 \pi G \rho_0$

$\Longrightarrow$ Valor crítico: $\omega^{2} = 0$ $\rightarrow$

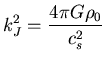$\displaystyle \rightarrow$ $\displaystyle k_J^{2} = \frac{4 \pi G \rho_0}{ c_s^{2}}$

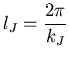$\displaystyle \rightarrow$ $\displaystyle l_J = \frac{2 \pi}{k_J}$

$\displaystyle \rightarrow$ $\displaystyle M_J \sim \rho_0 l_J^{3} \sim \rho_0^{-1/2} T^{3/2} \textrm{ (gas ideal).}$

$\Longrightarrow$ Inestabilidad (perturbaciones crecen exponencialmente en el tiempo)
$\fbox{\parbox[b]{4.cm}{ \begin{displaymath} M > M_J \end{displaymath}}}$

$\Longrightarrow$ Estimaciones: $l_J \approx 8 \times 10^{7} \rho^{-1/2} T^{1/2} cm.$ (gas ideal).
$\rightarrow$ Componente caliente y tenue: $l_J \approx 3 \times 10^{3} pc$
$\rightarrow$ Componente fría y densa: $l_J \approx 10 pc$

Nebulosas Oscuras (Medio Interestalar)

Propiedades Glóbulos Nubes

Pequeños Grandes Intermedias Grandes

$M/M_{\odot}$ $\ge$ 0.1 3 800 1.8 $\times 10^{4}$

R (pc) 0.03 0.25 4 20

n ( $H/cm^{3}$ ) $\ge$ 4 $\times$ $10^{4}$ 1.6 $\times 10^{3}$ 100 20

$\displaystyle \Longrightarrow$		$\displaystyle \vec{r} . \frac{d^{2} \vec{r}}{d t^{2}} = \frac{d}{dt} (\vec{r}. ... ...ac{d \vec{r}}{dt} = \frac{d^{2}}{dt^{2}} (\frac{r^{2}}{2} ) - \vec{v} . \vec{v}$
$\displaystyle \Longrightarrow$		$\displaystyle \int dm \left( \vec{r} . \frac{d^{2} \vec{r}}{d t^{2}} \right) = \frac{1}{2} \frac{d^{2} I}{dt^{2}} - 2 T$
$\displaystyle \Longrightarrow$		$\displaystyle \int dm \left( \vec{r} . \frac{\vec{\nabla} p}{\rho} \right) = \int dV \left(\vec{\nabla} . (p \vec{r}) - {p} \vec{\nabla} . \vec{r} \right) =$
		$\displaystyle = \int_{\sum} p \vec{r} . d \vec{\Sigma} - 3 \int p dV$

		$\displaystyle \frac{d^{2} r}{dt^{2}} = \frac{d v}{dr} \frac{d r}{dt} = \frac{1}{2} \frac{dv^{2}}{dr}$
$\displaystyle \Longrightarrow$		$\displaystyle \frac{1}{2} \frac{dv^{2}}{dr} = - \frac{G m}{r^{2}} \righta... ...c{v^{2}}{2} = G m \left(\frac{1}{r} - \frac{1}{r_0} \right) \rightarrow$
$\displaystyle \rightarrow$		$\displaystyle \left(\frac{2Gm}{r_0}\right)^{1/2} dt = \left(\frac{r_0}{r} - 1 \right)^{-1/2} dr \rightarrow$
$\displaystyle \rightarrow$		$\displaystyle \left(\frac{2Gm}{r_0}\right)^{1/2} t = (r_0 - r)^{1/2}... .../2} + r_0 arcsen \left(\frac{r_0 - r}{r_0} \right)^{1/2} \rightarrow$
$\displaystyle \rightarrow$		$\displaystyle \left(\frac{8 \pi G \rho_0}{3}\right)^{1/2} t = (1 - x)^{1/2} x^{1/2} + arcsen(1 - x)^{1/2} \rm {siendo} x\equiv r/r_0$

$\displaystyle \rightarrow$		$\displaystyle k_J^{2} = \frac{4 \pi G \rho_0}{ c_s^{2}}$
$\displaystyle \rightarrow$		$\displaystyle l_J = \frac{2 \pi}{k_J}$
$\displaystyle \rightarrow$		$\displaystyle M_J \sim \rho_0 l_J^{3} \sim \rho_0^{-1/2} T^{3/2} \textrm{ (gas ideal).}$

Propiedades		Glóbulos		Nubes
	Pequeños	Grandes	Intermedias	Grandes
$M/M_{\odot}$	$\ge$ 0.1	3	800	1.8 $\times 10^{4}$
R (pc)	0.03	0.25	4	20
n ( $H/cm^{3}$ )	$\ge$ 4 $\times$ $10^{4}$	1.6 $\times 10^{3}$	100	20

$\displaystyle \Longrightarrow$		$\displaystyle \frac{d^{2} r}{dt^{2}} = - \frac{G m(r)}{r^{2}} - \frac{1}{\rho} \frac{\partial p}{\partial r}$
$\displaystyle \Longrightarrow$		$\displaystyle t=0, r=r_0 , \displaystyle{\frac{d^{2} r}{dt^{2}}} = 0, \rho (r=r_0, t=0), = \rho_0 \rightarrow$
$\displaystyle \rightarrow$		$\displaystyle p (t=0) = k\rho_0^{\gamma} \equiv p_0$