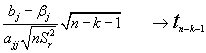
INFERENCIAS SOBRE EL MODELO LINEAL

Inferencia sobre un parámetro.

Contraste de hipótesis sobre un regresor.

Contrastes lineales sobre un conjunto de regresores.

Contraste de significación de los regresores.

Contraste de validez del modelo/ significación general/ Anova

Inferencias sobre un parámetro

Teniendo en cuenta los resultados anteriores resulta sencillo diseñar los métodos para la realización de inferencias sobre uno de los "regresores", b_j .

           Intervalo de confianza (1-a) para b_j:

               teniendo en cuenta que: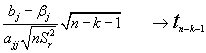

si llamamos S_bj al error standard del estimador ,esto es, a todo lo que divide a (bj-b_j) en la expresión anterior; el intervalo de confianza para bj resulta (para un N.C. de 1-a):

bjÎ [bj - t_a/2 S_bj ; bj + t_a/2 S_bj] con (1-a) de confianza

Para el caso particular del M.L.S. los intervalos de confianza para los coeficientes a y b serán respectivamente:

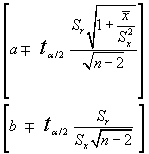
Ejemplo: En el ejemplo visto con anterioridad: El regresor para la primera variable explicativa (precio por kilo)e ra b₂=-1.44765.La raiz cuadrada del elemento 2,2 de (X'X)-1, a₂₂=(0.000746)1/2=0.027313,la "cuasi-desviación típica residual":S_r (n/n-k-1)^1/2= 8.451406,de forma que que el error standard del estimador es: S_b2= 0.230912

Si queremos construir un intervalo de confianza para un nivel del 99%: t_0.005 (12-2-1 g.l.)=3.25 de forma que el intervalo quedará:

b₂Î [-1.44765- 3.25. 0.230912 ; 1.44765+ 3.25. 0.230912 ]

b₂Î [-2.198114; 0.697186]

Contrastes de hipótesis sobre un regresor.

Basándonos en la distribución de (bj-bj)/ S_bj podremos igualmente contrastar hipótesis sobre el regresor bj

Si la hipótesis nula es: Ho: bj= bj* ya sea la alternativa uni o bilateral, el estadístico (bj-bj* )/ S_bj ,supuesta cierta la hipótesis nula tendrá una distribución t de Student(con n-k-1 g.l.) y podremos diseñar el contraste de la manera habitual que ya conocemos.

ejemplo

Contrastes lineales sobre un conjunto de regresores.

En muchos casos prácticos podemos estar interesado en contrastar una hipótesis no ya sobre el valor que toma un regresor,sino sobre cómo se comportan un conjunto de varios regresores.Si la hipótesis a contrastar consiste en que un conjunto de regresores verifican una cierta relación lineal esto puede llevarse a cabo a partir del procedimiento general que exponemos a continuación:

Una o varias relaciones lineales entre un conjunto de regresores puede expresarse de forma general de la siguiente manera:
Db = h

Donde el vector (k+1) dimensional b es el vector de parámetros (regresores) del modelo;h es un vector r-dimensional ,donde r es el número de relaciones lineales que estamos considerando; y, por último la matriz D de dimensión (r´k+1) es una matriz de coeficientes.

Así por ejemplo si queremos expresar sobre un modelo con 4 regresores (b₀,b₁,b₂,b₃)las siguientes 2 relaciones lineales:

b₁+b₂= 1 y b₁-2b₃= 0 podrá hacerse como:

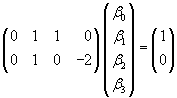
Teniendo en cuenta esto es facil ver que la hiótesis nula de que un conjunto de regresores verifican una o más relaciones lineales puede expresarse como:

H₀: Db = h

Es igualmente sencillo probar que si pre-multiplicamos el vector de estimadores b por la matriz D el resultado será un vector aleatorio

r-dimensional cuya distribución será normal ya que es una transformación lineal (forma lineal) del vector b que seguía una distrución normal:

(b --> N_k+1[ b ; s² (X'X)^-1])

El vector de medias del vector Db será E(Db)=DE(b)=Db=h (siempre que la hipótesis sea cierta).

y la matriz de varianzas será

Var (Db)= D.Var (b) D'= s² D(X'X)^-1D'

Así pues, si la hipótesis nula es cierta: Db --> N_r [ h , s² D(X'X)^-1D']

Puede apreciarse que la distribución de este estadístico vectorial depende del parámetro desconocido s .Para evitar este problema puede actuarse de la siguiente manera:

Aplicando el teorema de Cochran es inmediato que la forma cuadrática:

1/s². (Db-h)' [D(X'X)^-1D']^-1 (Db-h) sigue una c²   con r grados de libertad

Si consideramos que 1/s² . e'e sigue una c² con n-k-1 g.l.

y asumiendo la independencia entre ambas variables aleatorias:

                        el estadístico:

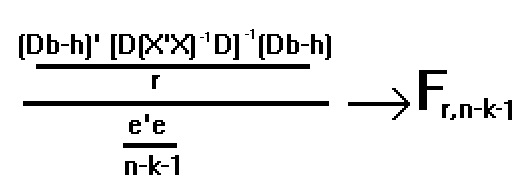
Bajo el supuesto de que la hipótesis nula es cierta.

Así pues evaluando este estadístico y comparandolo con el valor crítico correspondiente para el nivel de significación requerido:

si F > F_a rechazaremos la hipótesis que supone la presencia de esa relación lineal, y en caso contrario, la aceptaremos

ejemplo

Contrastes de significación de los regresores

Un tipo particularmente importante de contrastes de hipótesis sobre los regresores (ya sea sobre 1 o sobre varios de ellos) es el contraste de la hipótesis nula de que el (o los) regresor(es) considerado(s) son cero frente a la alternativa bilateral de que son distintos de cero.En estos casos, si llegamos a rechazar la hipótesis nula quedará establecido que el regresor es significativo queriendo decirse que existirá una relación lineal significativa entre la variable a explicar y la(s) variable(s) explicativa asociada al regresor (o regresores) sujeto(s) a debate.

Suele llamarse contraste de significación a este tipo de contraste.Cuando se trata de un contraste individual se llevará a cabo mediante un contraste t de Student bilateral.

Una medida de la significación o significatividad de un parámetro (regresor) suele darse a través del valor del nivel de significación necesario para rechazar la hipótesis de nulidad;de forma que cuanto más pequeño sea este valor más significativo es el regresor.

Un caso particular importante de los contrastes de significación es aquel en el que se consideran (a la vez)todos los regresores (excepción hecha del termino independiente).Este contraste constituye una prueba de la validez global del modelo y recibe el nombre de "contraste de significación general", de validez general (y, también de análisis de la varianza de la regresión)

Contraste de validez general (significación general)(ANOVA)

Como acabamos de comentar se trata de análizar la significación de todos los regresores a la vez, lo que equivale a analizar la validez general del modelo,la fuerza de la relación lineal existente entre la variable y y las variables x,la significación de la correlación lineal múltiple; todo ello es equivalente.

Como también hemos comentado se trata, en el fondo de contrastar la hipótesis:

H₀: b₁=b₂=b₃=. . . = b_k= 0

Podemos plantearlo, exactamente igual que el contraste general de hipótesis lineales sobre un conjunto de regresores.

H₀: Db = h

Aquí la matriz D sería la matriz identidad de orden k (con 1 elemento menos que el número total de parámetros k+1) y el vector h sería el vector 0 de orden k.

Pudiéndose expresar la hipótesis como:

H₀:I_kb = 0_k

y si llamamos b al vector de orden k formado por los regresores excluyendo el término independiente podemos expresar la hipótesis como: (igualmente a su estimador lo llamamos b y llamamos X a la matriz de los datos de x excluida la primera columna de unos)

H₀: b= 0

Al ser la matriz D la identidad y el vector h el vector cero, el estadístico del contraste quedaría:

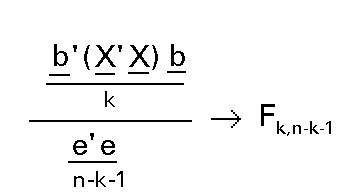
Si tenemos en cuenta que la regresión muestral era: Xb=y* y que pasaba por el centro de gravedad, entonces: b' X' X b será n veces la varianza debida a la regresión:

b' X' X b = n S²y*=n S²yR² . (Donde R² es el coeficiente de determinación muestral)

Por otro lado:e'e es n veces la varianza residual:

e'e= n Sr² = n Sy²(1- R²).

A partir de estos dos hechos es muy facil ver que el estadístico del contraste queda como:

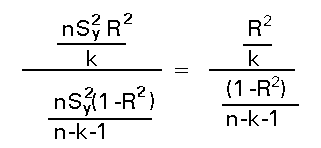
Que bajo el supuesto de la hipótesis nula seguirá una distribución F_k,n-k-1

Es interesante observar que en el caso del M.L.S. , con k=1, y ante la coincidencia del coeficiente de determinación y el cuadrado del coeficiente de correlación, nos encontramos con el estadístico del contraste de incorrelación, cuya distribución no probamos y aquí haya una demostración.

El planteamiento de este contraste admite un esquema ANOVA, en el siguiente sentido: La variación total (muestral) de la y (nS_y²) puede descomponerse en variación debida a la regresión

( b'X'Xb = n S²y*=n Sy²R² ) más la variación residual o no explicada

(e'e= n Sr² = n Sy²(1- R²)).