DISTRIBUCIÓN ![]() de PEARSON
de PEARSON
Esta distribución , junto con la t de Student y la F de Snedercor (además de la normal) son de fundamental importancia para el desarrolo de la inferencia estadística . Como las otras dos , es la distribución de una cierta característica de los datos obtenidos aleatoriamente a partir de una distribución normal . En consecuencia puede hacerse derivar de un proceso experimental de seleción aleatoria, aunque tambien puede ponerse en relación con las distribuciones Eulerianas.
Se define la ![]() con n grados de libertad , como la distribución
que sigue la variable suma de los cuadrados de n variables normales (tipificadas) [0;1]
independientes.
con n grados de libertad , como la distribución
que sigue la variable suma de los cuadrados de n variables normales (tipificadas) [0;1]
independientes.
Así , dadas n variables aleatorias independientes ![]() tales que :
tales que :
![]()
![]() las variables
las variables 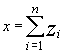 seguirá una
seguirá una ![]() con n grados de libertad.
con n grados de libertad.
Dado que la ![]() es la suma de n normales tipificadas al cuadrado podemos
afirmar , por el motivo de ser precisamente cuadrados ,que el campo de
actuación-variación de la variable así distribuída será siempre positivo .La forma de
la función de densidad y distribución variarán según los grados de libertad , siendo
su forma habitual la campaniforme, así
es la suma de n normales tipificadas al cuadrado podemos
afirmar , por el motivo de ser precisamente cuadrados ,que el campo de
actuación-variación de la variable así distribuída será siempre positivo .La forma de
la función de densidad y distribución variarán según los grados de libertad , siendo
su forma habitual la campaniforme, así
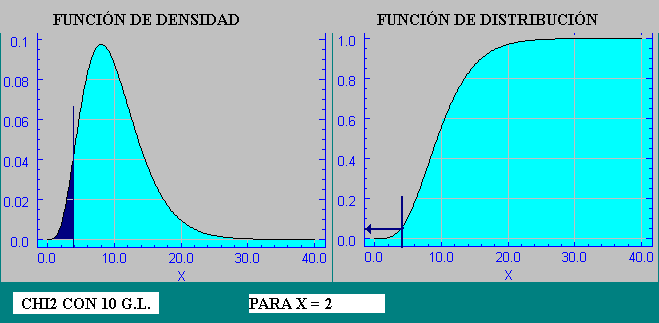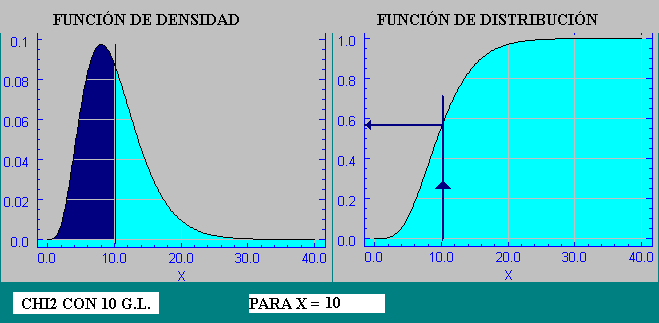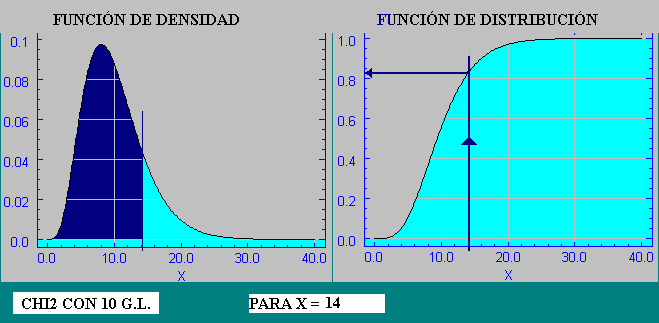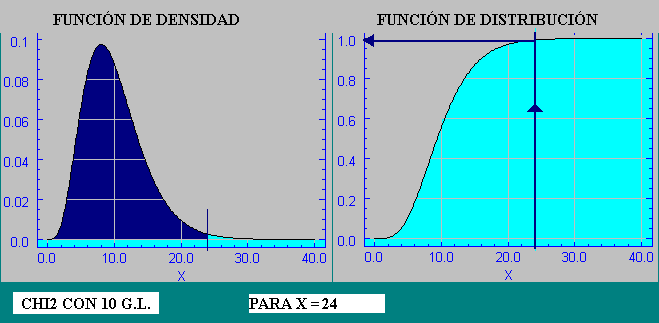
El cálculo de las diversas probabilidades para los diferentes valores de la variable X , se explicita normalmente en tablas desarrolladas para los diversos valores de grados de libertad ; nosotros planteamos un script (programa) para su cálculo directo . (Ir a script de la chi2)
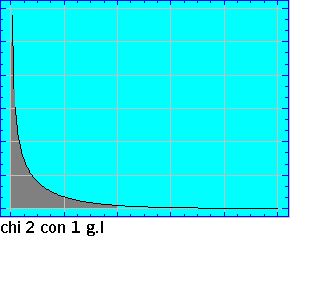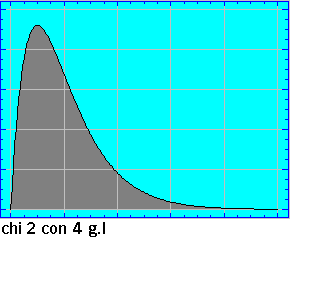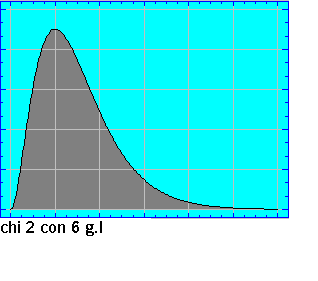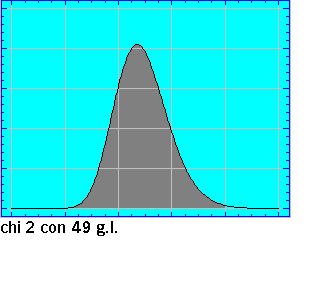 Como hemos dicho ,la representacíón grafíca de la
distribución ( su forma) varía según los valores que tome su parámetro n (grados
de libertad); así y como puede observarse en el gráfico animado , para grados de
libertad bajos ( sobre todo para un g.l.) el conjunto de la probabilidad queda muy
próxima al valor cero de la variable ; de esta característica surge , para algunos tipos
de contrastes que utilizan la Chi2 , la corrección
de Yates
Como hemos dicho ,la representacíón grafíca de la
distribución ( su forma) varía según los valores que tome su parámetro n (grados
de libertad); así y como puede observarse en el gráfico animado , para grados de
libertad bajos ( sobre todo para un g.l.) el conjunto de la probabilidad queda muy
próxima al valor cero de la variable ; de esta característica surge , para algunos tipos
de contrastes que utilizan la Chi2 , la corrección
de Yates
La función de densidad de la ![]() vendrá dada por :
vendrá dada por :
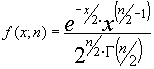 :
:
siendo ![]() una distribución gamma de Euler
de parémetro
una distribución gamma de Euler
de parémetro ![]() y
y
siendo n ( número de grados de libertad) el
único párametro de la distribución ![]()
La función generatriz de momentos vendrá dada por
![]() partiendo de ella podemos establecer, por aplicación del teorema de los momentos ,que la media vendrá
establecida en
partiendo de ella podemos establecer, por aplicación del teorema de los momentos ,que la media vendrá
establecida en ![]() siendo la varianza
siendo la varianza ![]()
La distribución JHI-2 (chi 2) cumple el teorema de adición para su parámetro n (grados de libertad) , así la suma de dos chi2 con n y m grados de libertad respectivamente , no será otra cosa que una chi2 con (n+m) grados de libertad . Es lógico pensar que si una chi2 con n grados de libertad es la suma de n normales tipificadas(independientes) al cuadrado ; y que una chi2 con m grados de libertad es la suma de m normales tipificadas(independientes) al cuadrado , la suma de ambas será , obviamente, la suma de (m+n) normales tipificadas (independientes) al cuadrado : es decir, una chi2 con (n+m) grados de libertad.