Teorema Central del Límite ; convergencia de la distribución de Poisson

Realmente se trata de un caso particular de aplicación del T.C.L. forma Lindeberg-Lévy ; la particularidad reside en que las variables aleatorias que forman la sucesión son o se distribuyen según una Poisson de parámetro l . El hecho de que lo tratemos aquí radica en su utilidad y practicidad , y así:

Dada una sucesión de variables aleatorias {X_n}    donde X_i ® Poisson(l ) por lo que la media común es l y su varianza común , también

        En aplicación del TCL tendremos que

            La sucesión definida como :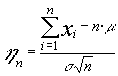

                                                converge en distribución a una N[0,1]

Dado que la distribución de Poisson cumple el teorema de adición para el parámetro l , tendremos que:

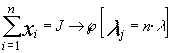                 de donde conoceremos que
        y la desviación típica será

                    por lo que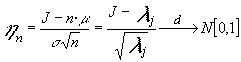

De donde se deduce que una distribución de Poisson cuando l tiende a infinito converge a una normal con media l y desviación típica raíz de l