Teorema de Glivenko-Cantelli (ley fuerte de los grandes números)
Si consideramos una muestra
como una sucesión de variables aleatorias {Xn}
que procede de ser un subconjunto
de la población , tomada ésta como otra sucesión de tamaño mayor
(máximo-completa-segura) . Evidentemente con la misma función de probabilidad para todas
las variables de la sucesión (muestra) ; el teorema de Glivenko-Cantelli nos indica que
la función de distribución de probabilidad común a las variables de la sucesión
muestra , convergen de manera "casi segura" a la
verdadera función de distribución de la población , así :
Si denominamos DI a las
máximas diferencias que pueden existir entre los valores que proporciona una función de
distribución (muestra-sucesión) y otra (función de distribución de la población)
tendremos que se cumple que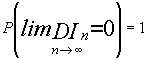 
luego 