Convergencia de sucesiones de variables aleatorias.
Convergencia
casi-segura
Convergencia en
probabilidad
Convergencia en media
cuadrática
Convergencia en ley ( o
distribución)
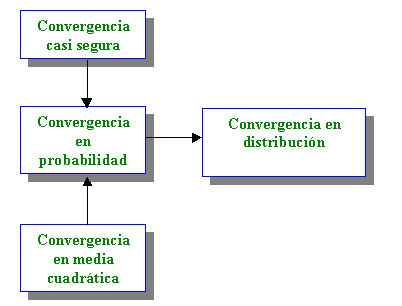
Relaciones de implicación entre los diversos tipos de
convergencia
Consideramos una sucesión infinita de variables aleatorias {Xn} : {X1,X2,…,Xn,…}
Donde cada Xi es una variable aleatoria con su correspondiente distribución de probabilidad. , puede darse el caso que la sucesión converja a una variable aleatoria (límite) X , con una distribución de probabilidad asociada.
Por ejemplo: {Xn} con Xn ® B(n,p) para n=1,2,….
Así, y definidas todas las variables aleatorias que componen la sucesión sobre el mismo espacio probabilístico ; dicha sucesión podrá converger a una variable aleatoria X de distintas maneras o tipos :
Convergencia casi-segura
Convergencia en probabilidad
Convergencia en media cuadrática
Convergencia en ley ( o distribución)
Así :
Una sucesión de variables
aleatorias, {Xn} , converge con probabilidad 1, o de forma casi segura,
a una variable aleatoria X ( que puede degenerar en una constante K) cuando se cumple que:
![]()
Una
sucesión de variables aleatorias, {Xn} , converge en probabilidad ,
a una variable aleatoria X ( que puede degenerar en una constante K) cuando se cumple que:
"e
>0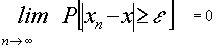
o bien considerando su complementario
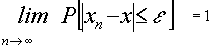
de esta forma interpretaremos que ![]()
cuando en el límite , la probabilidad de que sucesión de variables aleatorias y aquella
a la que converge difieran (en valor absoluto) en un valor mayor e (pequeño) es cero ( o complementariamente).
Ha de tenerse en cuenta en este caso que la
sucesión sólo implica a la sucesión de las probabilidades de los sucesos y no a las
variables en sentido matemático
Una sucesión de variables aleatorias, {Xn} , converge en media cuadrática,
a una variable aleatoria X (que puede degenerar en una constante K) cuando se cumple que:
![]()
de esta forma interpretaremos que ![]()
cuando en el límite , la dispersión de la sucesión de variables aleatorias tomando como
origen de ésta la variable a la que converge , es 0. Es de importancia notar que
pueden plantearse diversos tipos de convergencias en media dependiendo del orden r del
exponente (en este caso 2)
Una sucesión de variables aleatorias, {Xn} , converge en ley o en
distribución
a una variable aleatoria X , cuando se cumpla alguna de las siguientes condiciones , en el
convencimiento de que si se cumple una se cumplirán las restantes :
a) Si para toda función real g se verifica que :
![]()
b)
Si para todo número real t se cumple que : ![]()
c)
Si para todo par de puntos a y b ; tales que b > a se cumple que :
![]()
![]()
de esta forma interpretaremos que ![]()
cuando en el límite el comportamiento de la función de distribución de la sucesión de
variables aleatorias y la de aquella a la que converge son iguales .
Existen relaciones de implicación (demostrables) entre los diversos tipos de convergencia :
Así :
La convergencia en media cuadrática implica la convergencia en probabilidad , no siendo cierto (generalmente) el comportamiento inverso :
Luego ![]()

![]()
La convergencia casi
segura implica la convergencia en probabilidad , no siendo cierto (generalmente) el
planteamiento inverso :
Luego ![]()

![]()
La convergencia en
probabilidad implica la convergencia en distribución , no siendo cierto (generalmente) el
planteamiento contrario :
Luego ![]()

![]()
Esquemáticamente quedaría :