ESTIMACIÓN PUNTUAL
ESTIMACIÓN PUNTUAL
1.Introducción:Estimación y Estimador
En este tema se analizan las formas adecuadas para el establecimiento del conocimiento numérico o abstracto de un parámetro de una población , y que evidentemente nos es desconocido , partiendo ,claro está, de la información suministrada por la muestra.
LA ESTIMACION , como
proceso, consiste en que dada una población que siga una distribución de cierto tipo con
función de probabilidad (de cuantía o de densidad) f( X,
) dependiente de un parámetro
o varios desconocido(s) " ", aventurar en base a los datos muestrales el valor que toma o puede
tomar el parámetro o parámetros .
UN ESTIMADOR 
(x) es una
función de una muestra genérica
x=[x 1,x2 , ,...,x n ], es decir , un estadístico que utilizaremos para estimar el valor del parámetro . Por tanto es una variable aleatoria y será necesario para la estimación conocer la distribución muestral del estimador.
UNA ESTIMACION será el valor concreto que
tomará el estimador al aplicar la muestra concreta obtenida y será ,por tanto ,la
solución concreta de nuestro problema. (Cuando no haya lugar para la confusión
designaremos al estimador, a veces, como en vez de (x) )
LA TEORIA DE LA ESTIMACION se ocupará, dentro del marco de la perspectiva clásica, de estudiar las características deseables de los estimadores permitiéndonos escoger aquel estimador que reúna más propiedades ventajosas para que realicemos buenas estimaciones .
2.Propiedades de los Estimadores
INSESGADEZ: un estimador es insesgado o centrado cuando verifica que
E( ) = . (Obsérvese que deberíamos
usar (x)
y no , pues hablamos de estimadores y no de estimaciones pero como no cabe
la confusión ,para simplificar , aquí , y en lo sucesivo usaremos ) . En caso contrario se dice
que el estimador es sesgado . Se llama sesgo a
[se designa con B de BIAS ,sesgo en inglés]
Como ejemplo podemos decir que : la media muestral es un estimador insesgado de la media de la población (y lo es sea cual fuere la distribución de la población) ya que:
si el parámetro a estimar es
y establecemos como estimador de
tendremos que 
luego la
media muestral es un estimador insegado de la media poblacional.
En cambio la varianza muestral es un estimador
sesgado de la varianza de la población , ya que: si utilizamos como estimador de 
la varianza muestral 
es decir : 
tendremos que 
que es el
parámetro a estimar .
existe pues un sesgo que será
Dado que la varianza muestral no es un estimador de la varianza poblacional con propiedades de insesgadez , conviene establecer uno que si las tenga ; este estimador no es otro que la cuasivarianza muestral , de ahí su importancia ;así
la cuasivarianza es en función de la varianza
y tomada como estimador
tendríamos que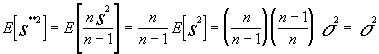 
dado que la esperanza del estimador coincide con el parámetro a estimar podemos decir que la cuasivarianza muestral es un estimador insesgado de la varianza de la población.
No obstante , y dado que ,cuando el tamaño de la muestra tiende a infinito el sesgo tiende a cero, se dice que el estimador es asintóticamente insesgado o asintóticamente centrado: podemos establecer que :
Por tanto la
varianza muestral es un estimador sesgado pero asintóticamente insesgado de la varianza
de la población.
CONSISTENCIA
. Un estimador es consistente si converge en probabilidad al parámetro a estimar . Esto es:
si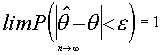 
LINEALIDAD.
Un estimador es lineal si se obtiene por combinación lineal de los elementos de la muestra ; así tendríamos que un estimador lineal sería :
EFICIENCIA.
Un estimador es eficiente u óptimo cuando posee varianza mínima o bien en términos relativos cuando presenta menor varianza que otro . Quedando claro que el hecho puede plantearse también en términos más coherentes de Error Cuadrático Medio (ECM). Tendríamos que :
ECM(
) =
por lo expresado podemos
aventurar que un estimador insegado , luego 
es el único capaz de generar eficiencia. (ir a cota de Cramer-Rao)
SUFICIENCIA . Un
estimador es suficiente cuando 
no depende del
parámetro a estimar .
En términos más simples : cuando se aprovecha toda la información muestral. (ir a teorema de
caracterización Neyman-Fisher)
MÉTODO POR ANALOGÍA. Consiste en aplicar la misma expresión formal del parámetro poblacional a la muestra , generalmente , estos estimadores son de cómoda operatividad , pero en ocasiones presentan sesgos y no resultan eficientes . Son recomendables , para muestras de tamaño grande al cumplir por ello propiedades asintóticas de consistencia.
METODO DE LOS MOMENTOS. Consiste en tomar como estimadores de los momentos de la población a los momentos de la muestra . Podríamos decir que es un caso particular del método de analogía. En términos operativos consiste en resolver el sistema de equivalencias entre unos adecuados momentos empíricos(muestrales) y teóricos(poblacionales).
Ejemplo :
conocemos que la media poblacional de una determinada variable x depende de un parámetro K que es el que realmente queremos conocer (estimar). Así
por el método de los momentos tendríamos
que
de donde 
ESTIMADORES MAXIMO-VEROSIMILES. La verosimilitud consiste en otorgar a un estimador/estimación una determinada "credibilidad" una mayor apariencia de ser el cierto valor(estimación) o el cierto camino para conseguirlo(estimador).
En términos probabilísticos podríamos hablar de que la verosimilitud es la probabilidad de que ocurra o se dé una determinada muestra si es cierta la estimación que hemos efectuado o el estimador que hemos planteado.
Evidentemente , la máxima verosimilitud , será aquel estimador o estimación que nos arroja mayor credibilidad .En situación formal tendríamos :
Un estimador máximo-verosímil es el que se obtiene maximizando la función de verosimilitud (likelihood) de la muestra
Que es la función de probabilidad (densidad o cuantía) que asigna la
probabilidad de que se obtenga una muestra dependiendo del (o de los)parámetro(s) " " pero
considerada como función de . Si la distribución de la población es tal que su densidad
depende de uno o más parámetros 
, la probabilidad (densidad) de cada
realización muestral xi
(con i=1,2,..,n) será: 
y, a partir de aquí podremos obtener la
función de verosimilitud de la muestra
Si el muestreo es simple:
por ser independientes cada una de las realizaciones muestrales.
El estimador que maximice
será el estimador máximo-verosímil (E.M.V.) Y será aquel valor/expresión para el que se verifique la derivada :
Si lo planteado fuera EMV de varios parámetros 
las expresiones serían. .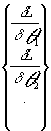 
Debido a que la función de verosimilitud es a fin de cuentas una función de probabilidad ,será una función definida no negativa y por lo tanto alcanzará su máximo en los mismos puntos que su logaritmo . Por esta razón suele maximizarse
en lugar de la propia función de verosimilitud . Suele hacerse esto en todos aquellos casos en los que la función de verosimilitud depende de funciones exponenciales.
Obtener el E.M.V. del parámetro l de una distribución de Poisson
Para una muestra de tamaño n tendremos que la función de de verosimilitud será:
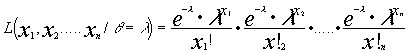
maximizar L será equivalente a maximizar el numerador de L
si llamamos L' a dicho numerador y tomamos logaritmos tendremos que es
tomando logaritmos 
maximizando dicho logaritmo :
uego el estimador máximo verosímil de 
En una población normal estimar por el método de máxima
verosimilitud los parámetros 
.
la función de verosimilitud será:
·
······
=
= 
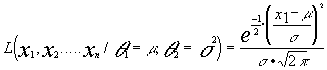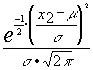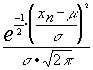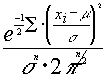
maximizar L es equivalente a maximizar ln L .
Maximizando :
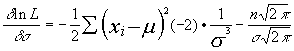= 0
despejando : de la primera : 
de la segunda : 
el estimador(MV) de la media poblacional será la media de la población mientras que el
de la varianza poblacional corresponderá a su homónima muestral . Ambos estimadores
reúnen casi-todas las propiedades salvo en el caso de la varianza muestral que es
asintóticamente insesgada.