ir a intervalos  
ir a scripts de realización

   Dado un nivel de confianza 1 - a ,   conocemos que el intervalo de confianza para la media de una distribución normal
                    con varianza conocida es :

                            Podemos establecer el error "e" como la amplitud del intervalo es decir :

                                  determinar , por tanto, el tamaño muestral consistirá en:
  una vez establecido el error que se quiere cometer ,despejar "n" de la expresión que anteriormente hemos establecido :
                                    así                

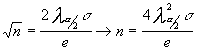
Hemos indicado que el error e , es la amplitud del intervalo ; en muchos manuales se especifica como e=el semi-intervalo ó la semi-holgura . Que no es más que lo mismo, pues dos veces la semi-holgura es , evidentemente , la holgura total , por tanto su amplitud. En otros se trata al error  , e,  como simplemente la semi-holgura ; la semi-amplitud. Lógicamente todos los planteamientos son correctos ; solo hemos de poner cuidado a la hora de concluir la expresión correcta del tamaño muestral .

Así : un error de e=4 supone un error=amplitud del intervalo=8 y el error medido como semi-amplitud sería de 4.

Para todos los intervalos que hemos visto es posible el cálculo del tamaño muestral si prefija el error admisible ; no vamos a realizar el desarrollo de todos .Nos centramos por su importancia en el tamaño muestral necesario para la construcción de un intervalo de confianza para la proporción de una característica con un determinado error prefijado , así

Si establecemos construir un intervalo de confianza para la p de una característica con un determinado nivel de confianza 1-a  ; y un determinado error "e" de un tanto por uno ; y con muestreo aleatorio simple . Tendremos que :

              dado que el intervalo es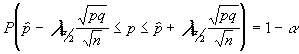        

                   y dado que el error es   e = a mplitud del intervalo   =   despejando n

                           obtendríamos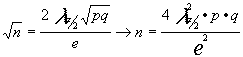          

Como es habitual el cálculo de n se realiza previamente al muestreo y precisamente se realiza el muestreo para conseguir información sobre la proporción p con la que se da una característica en una población , por lo que parece difícil que se conozca dicha p necesaria para conseguir el tamaño muestral para estimar precisamente p , de ahí que poniéndonos en el caso más desfavorable (varianza poblacional máxima) tomemos p=q=0.5 ; habitual precisión que se hace en las fichas técnicas de las encuestas.

Recurrentemente y por facilidad operativa suele plantearse, para este tipo de cálculos de tamaños muestrales , el nivel de confianza en el 95,5 % , la razón es que los valores de  ; (ir a tabla de la normal) por lo que para una semi-holgura determinada de error la expresión sería la                 
                                     siendo ,recordemos ,     la semi-amplitud en tanto por uno.

Calcular el tamaño muestral necesario para llevar a cabo un m.a.s. para determinar un intervalo para la proporción de personas vegetarianas si el error que estamos dispuestos a admitir es del más menos 3%. A) nivel de confianza 90%. B) nivel de confianza 95.5%.

A)          e=     amplitud del intervalo            (ir a script de realización)

              nivel de confianza 1-a =0.9      por lo que (ir a tabla de la normal)   1.645    
                                     luego tomando   p=q=0.5

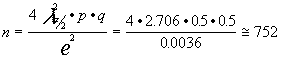
B)             la semi-holgura sería 0.03 semi-amplitud                        (ir a script de realización)

                                nivel de confianza 1-a =0.995   por lo que    (ir a tabla de la normal)

                       así                     

Si el intervalo a construir parte de un muestreo irrestricto (sin reemplazamiento) el cálculo del tamaño muestral partiría de la expresión: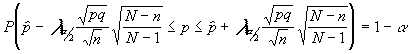 

conocido el error "e" que estamos dispuestos a conocer y conocida también la población (su tamaño), N, así como el nivel de confianza . Tendríamos que

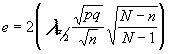                                                     de donde despejaríamos n para conseguir el tamaño muestral. Es evidente que es mucho más cómodo despejar n para cada caso específico que plantear una expresión general , por lo que recomendamos que así se haga . Las afirmaciones que se vertieron sobre "p" y su valor en el caso de m.a.s. son de aplicación , también ,en este caso. (ir a script de realización para p=q=0.5)       (ir a script de realización para información sobre p)