CONTRASTES DE UNA COLA

ir a contrastes
scripts (funcionan de manera bilateral y unilateral)

Hasta ahora hemos visto visto contrastes en los que la hipótesis nula era una hipótesis simple (la hipótesis de que el parámetro tomase un determinado valor), que se enfrentaba a la hipótesis alternativa (compuesta) (lo que equivalía a no establecer una alternativa concreta a la hipótesis sujeta a contraste).

Sin embargo,en muchos casos prácticos concretos nos interesará contrastar  

frente a la hipótesis alternativa de o bien

Cuando nos interese saber si podemos considerar que y nos vaya a reportar las mismas,o aún mejores , consecuencias el que , nos interesará hacer el contraste
Cuando nos interese saber si podemos considerar que y nos vaya a reportar las mismas ,o aún mejores consecuencias el que ,nos interesará hacer el contraste

En estos dos nuevos casos la base teórica para la decisión de aceptación o no de H ₀ va a ser la misma que en el caso ya estudiado de Pero, en la medida en que el rechazo de la hipótesis nula supone la aceptación de una hipótesis alternativa bien diferente ,el diseño de los criterios de aceptación van a diferir :va a diferir la construcción de la región crítica y de la región de aceptación (no rechazo).

De esta manera. Dado un nivel de significación , prefijado, trabajaremos con la distribución muestral de un estadístico adecuado ,T, cuya distribución dependa del parámetro sujeto a contraste para determinar la región crítica y de aceptación ,de forma que, como en el caso ya estudiado:

La región de aceptación verifique que y la región crítica que ,siendo, evidentemente, ambas complementarias.
Si los datos muestrales concretos son tales que: no rechazamos H₀

mientras que si rechazamos H₀ luego aceptamos H₁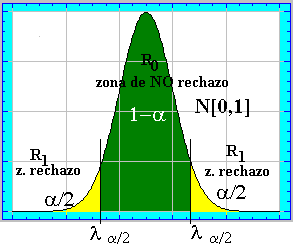

En el caso estudiado anteriormente, en el medida en que la distribución de T solía ser simétrica y en la que, como es lógico, estábamos interesados en hacer constrastes "duros"(severos con la hipótesis nula) elegíamos de todos los posibles pares de regiones "aceptación / crítica" precisamente aquél que nos ofrecía una región crítica de mayor amplitud y una región de aceptación de menor amplitud. Esto nos llevaba a elegir el intervalo centrado de probabilidad 1-a como región de aceptación, y como región crítica (zona de rechazo) las dos colas simétricas de probabilidad a /2.
En la medida en que rechazar suponía aceptar y teniendo en cuenta que la mayor parte de las distribuciones de los estadísticos están centradas en el auténtico valor del parámetro, esta determinación de las zonas de aceptación y rechazo era consecuentemente consistente con las características de nuestro contraste: un resultado muestral alejado de la zona central tanto por la izquierda como por la derecha nos da cuenta de que q debe ser significativamente distinto de q ₀ (por defecto o por exceso). El rechazo de H₀ supone aceptar que q ¹ q ₀ , e igual nos da que lo más verosímil sea que q > q ₀ (los datos muestrales caen en la cola de la derecha) que sea q < q ₀ (los datos muestrales caen en la cola de la izquierda).

Sin embargo al considerar el contraste del tipo :
el hecho que los datos muestrales (valor de T) caigan en la región critica R₁ nos lleva a considerar más verosímil H₁ , y, evidentemente, sólo es más verosímil H₁ frente a H₀ si los datos muestrales difieren significativamente por defecto de la zona central.

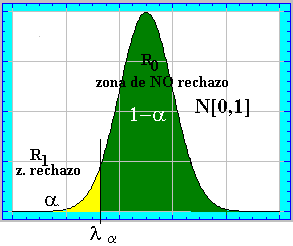
Esta argumentación nos conduce a que diseñemos una región crítica de "una sola cola" (cola de la izquierda). Región crítica que, recordemos debe seguir verificando que
. Es decir :

Ante el ejemplo de contraste :

H : µ = µ₀
H : µ < µ₀

En una población normal y varianza conocida para muestreo aleatorio simple con un determinado nivel de significación ; tendremos que si el estadístico   T=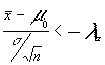      rechazaremos H₀ luego aceptaremos H₁
                   en caso contrario si T=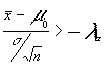 no rechazaremos H₀
Evidentemente si esto ocurre con el contrate especificado de ésta manera será por analogía lo contrario en el caso de plantearse el contraste de la siguiente forma :

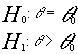                   Así que los datos muestrales den lugar a un valor que se encuentre en la región crítica R₁ , nos lleva considerar más verosímil H₁ y ,lógicamente , sólo es más verosímil H₁ frente a H₀ si los datos muestrales difieren significativamente por exceso de la zona central.

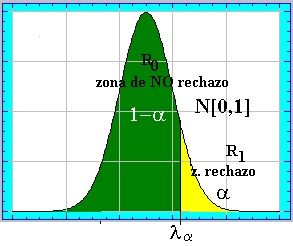
De forma análoga al caso anterior, esta argumentación nos conduce a que diseñemos una región crítica "de una sola cola" (cola de la derecha). Región crítica que deberá seguir cumpliendo que

y, por tanto, la región de aceptación será su complementaria y cumplirá que

Así, por ejemplo, ante un contraste:

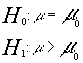
                             en una población normal con varianza desconocida y muestra pequeña

                                si   T=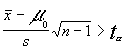     rechazaremos la hipótesis nula aceptando la alternativa

en cambio si T=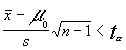       no rechazaremos la hipótesis nula rechazando ,obviamente , la alternativa de que la media es mayor que el valor hipotético planteado. Evidentemente en este caso las zonas de aceptación y rechazo parten de la t de Student ( n-1 grados de libertad) pues , como ya vimos , es lo debe utilizarse si la población es normal , conocemos la varianza y la muestra es pequeña.  (ir a ejemplo)