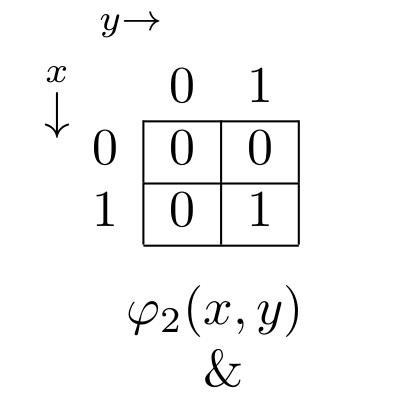\documentclass[titlepage]{amsbook}
\usepackage{amsbsy,amsmath,amssymb}
\usepackage{tikz}
\begin{document}
\begin{center}
{\Large Wahrheitstabelle}
\vspace*{2cm}
\begin{tabular}{ccccccccc}
%%%NEGACIÓ
\begin{tikzpicture}
\node (mat) at (0,0) {
$\begin{array}{cc}
\\
\cline{2-2}
0 & \multicolumn{1}{|r|}{1} \\
\cline{2-2}
1 & \multicolumn{1}{|r|}{0} \\
\cline{2-2}\end{array}$};
\node (x) at (-0.85, 0.35) {${\overset{x}{\downarrow}}$};
\end{tikzpicture}
&&
%%%CONJUNCIÓ
\begin{tikzpicture}
\node (mat) at (0,0){
$\begin{array}{ccc}
& 0 & 1 \\
\cline{2-3}
0 & \multicolumn{1}{|r|}{0} & \multicolumn{1}{r|}{0} \\
\cline{2-3}
1 & \multicolumn{1}{|r|}{0} & \multicolumn{1}{r|}{1} \\
\cline{2-3}\end{array}$};
\node (x) at (-0.85, 0.35) {${\overset{x}{\downarrow}}$};
\node (y) at (-0.35, 0.85) {$\scriptstyle{y\rightarrow}$};
\end{tikzpicture}
&&
%%%DISJUNCIÓ
\begin{tikzpicture}
\node (mat) at (0,0) {
$\begin{array}{ccc}
& 0 & 1 \\
\cline{2-3}
0 & \multicolumn{1}{|r|}{0} & \multicolumn{1}{r|}{1} \\
\cline{2-3}
1 & \multicolumn{1}{|r|}{1} & \multicolumn{1}{r|}{1} \\
\cline{2-3}\end{array}$};
\node (x) at (-0.85, 0.35) {${\overset{x}{\downarrow}}$};
\node (y) at (-0.35, 0.85) {$\scriptstyle{y\rightarrow}$};
\end{tikzpicture}
&&
%%%IMPLICACIÓ
\begin{tikzpicture}
\node (mat) at (0,0) {
$\begin{array}{ccc}
& 0 & 1 \\
\cline{2-3}
0 & \multicolumn{1}{|r|}{1} & \multicolumn{1}{r|}{1} \\
\cline{2-3}
1 & \multicolumn{1}{|r|}{0} & \multicolumn{1}{r|}{1} \\
\cline{2-3}\end{array}$};
\node (x) at (-0.85, 0.35) {${\overset{x}{\downarrow}}$};
\node (y) at (-0.35, 0.85) {$\scriptstyle{y\rightarrow}$};
\end{tikzpicture}
&&
%%%DOBLE IMPLICACIÓ
\begin{tikzpicture}
\node (mat) at (0,0) {
$\begin{array}{ccc}
& 0 & 1 \\
\cline{2-3}
0 & \multicolumn{1}{|r|}{1} & \multicolumn{1}{r|}{0} \\
\cline{2-3}
1 & \multicolumn{1}{|r|}{0} & \multicolumn{1}{r|}{1} \\
\cline{2-3}\end{array}$};
\node (x) at (-0.85, 0.35) {${\overset{x}{\downarrow}}$};
\node (y) at (-0.35, 0.85) {$\scriptstyle{y\rightarrow}$};
\end{tikzpicture}
\\ %%%FINAL DE LA PRIMERA LÍNIA
$\ \ \ \ \ \varphi_1(x)$
&&
$\ \ \ \ \ \varphi_2(x,y)$
&&
$\ \ \ \ \ \varphi_3(x,y)$
&&
$\ \ \ \ \ \varphi_4(x,y)$
&&
$\ \ \ \ \ \varphi_5(x,y)$
\\ %%%FINAL DE LA SEGONA LÍNIA
$\ \ \ \ \ \ \sim$
&&
$\ \ \ \ \ \ \&$
&&
$\ \ \ \ \ \ \vee$
&&
$\ \ \ \ \ \ \rightarrow$
&&
$\ \ \ \ \ \ \leftrightarrow$
\\ %%%FINAL DE LA TERCERA LÍNIA
\end{tabular}
\end{center}
\end{document}