Recull de qüestions

Àlgebra Lineal i Geometria I – 2015/2023

Les qüestions recopilades en aquest recull han estat proposades pels professors i professores responsables de l’assignatura d’Àlgebra Lineal i Geometria I del Grau en Matemàtiques i del Doble Grau en Física i Matemàtiques de la Universitat de València i han aparegut com a preguntes d’examen d’aquesta assignatura o com a qüestions proposades al Programa d’Estudiants Correctors de la Facultat de Ciències Matemàtiques de la Universitat de València.

Podeu descarregar els enunciats d’aquest recull.
Podeu proposar les vostres solucions enviant per correu el corresponent codi $LATEX$.

1. Sistemes d’equacions

Qüestió 1.1

Siga $\mathsf{A}\in {\mathrm{M}}_n(\mathbb{K})$ una matriu de rang $n$ i $\mathsf{B}\in {\mathrm{M}}_{n,1}(\mathbb{K})$. És cert que el sistema d’equacions $\mathsf{AX}=\mathsf{B}$ és compatible?

Solució

Notem que $\mathrm{rang}(\mathsf{A})\le \mathrm{rang}(\mathsf{A}\mid \mathsf{B})\le \mathrm{rang}(\mathsf{A})+1$. A més, com la matriu ampliada $[\mathsf{A}\mid \mathsf{B}]$ en aquest cas és una matriu en ${\mathrm{M}}_{n,n+1}(\mathbb{K})$, trobem que $\mathrm{rang}(\mathsf{A}\mid \mathsf{B})\le n$.

Com, per hipòtesi, $\mathrm{rang}(\mathsf{A})=n$, concloem que $\mathrm{rang}(\mathsf{A})=\mathrm{rang}(\mathsf{A}\mid \mathsf{B})=n$.

Així, per Rouché-Frobenius, el sistema és compatible determinat.

– Andrea Muñoz Ros.

Qüestió 1.2

Siga $\mathsf{AX}=\mathsf{B}$ l’expressió matricial d’un sistema d’$n$ equacions amb $m$ incògnites. És cert que si $n\le m$ aleshores el sistema no és compatible determinat? Justifica la resposta.

Solució

Un sistema d’aquest tipus pot ser compatible determinat. Així la proposició no és certa. Si $n=m$ i $\mathrm{rang}(\mathsf{A})=\mathrm{rang}(\mathsf{A}\mid \mathsf{B})=m$ aleshores, per Rouché-Frobenius, tindrem un sistema compatible determinat.

– Paula Domènech Tomàs.

Qüestió 1.3

Dóna dos sistemes d’equacions sobre un cos $\mathbb{K}$ amb la mateixa matriu de coeficients de forma que un dels sistemes siga compatible i l’altre incompatible.

Solució

Es consideren els sistemes $\mathcal{S}$ i $\mathcal{T}$ sobre $\mathbb{R}$, on $$\begin{array}{ccccc}\begin{array}{rcl}x+y& =& 1\\ 2x+2y& =& 2\end{array}\}& (\mathcal{S})& & \begin{array}{rcl}x+y& =& 1\\ 2x+2y& =& 3\end{array}\}& (\mathcal{T})\end{array}$$ Són sistemes que tenen la mateixa matriu de coeficients. El sistema $\mathcal{S}$ és compatible indeterminat i el sistema $\mathcal{T}$ és incompatible.

– Marta Ribera Ramos.

Qüestió 1.4

Defineix matriu esglaonada reduïda per files.

Solució

Una matriu és esglaonada per files si:

1. La primera entrada no nul·la de cada fila és un $1$. A aquesta entrada l’anomenarem pivot.

2. El pivot de cada fila es troba estrictament a la dreta dels pivots de les files anteriors.

3. Si alguna fila és nul·la, aquesta es troba baix del tot.

Direm que una matriu esglaonada per files és esglaonada reduïda per files si, a més,

4. Les entrades que queden per damunt de cada pivot són $0$.

– Marta Ribera Ramos.

Qüestió 1.5

Siga $\mathcal{S}$ un sistema d’$m$ equacions lineals amb $n$ incògnites sobre $\mathbb{R}$ que admet dues solucions diferents. Demostra que $\mathcal{S}$ té infinites solucions i construeix-les explícitament a partir de les dues solucions donades.

Solució

Siga $\mathsf{AX}=\mathsf{B}$ la representació matricial del sistema $\mathcal{S}$. Suposem que ${\mathsf{X}}_1$ i ${\mathsf{X}}_2$ són dues solucions diferents del sistema $\mathcal{S}$. Així ${\mathsf{AX}}_1=\mathsf{B}$ i ${\mathsf{AX}}_2=\mathsf{B}$. Restant aquestes dues solucions trobem que ${\mathsf{X}}_1-{\mathsf{X}}_2$ és una solució no nul·la del sistema homomogeni associat a $\mathcal{S}$, ja que $$\mathsf{A}({\mathsf{X}}_1-{\mathsf{X}}_2)=\mathsf{B}-\mathsf{B}=\mathsf{0}.$$ Per a cada paràmetre $\lambda \in \mathbb{R}$, tindrem que $\lambda ({\mathsf{X}}_1-{\mathsf{X}}_2)$ també serà solució del sistema homomogeni associat, ja que $$\mathsf{A}(\lambda ({\mathsf{X}}_1-{\mathsf{X}}_2))=\lambda (\mathsf{B}-\mathsf{B})=\lambda \mathsf{0}=\mathsf{0}.$$ Finalment, per a cada paràmetre $\lambda \in \mathbb{R}$, definim ${\mathsf{X}}_{\lambda }={\mathsf{X}}_1+\lambda ({\mathsf{X}}_1-{\mathsf{X}}_2).$

Notem que ${\mathsf{X}}_{\lambda }$ és una solució del sistema $\mathcal{S}$, ja que $$\mathsf{A}{\mathsf{X}}_{\lambda }=\mathsf{A}({\mathsf{X}}_1+\lambda ({\mathsf{X}}_1-{\mathsf{X}}_2))=\mathsf{B}-\lambda \mathsf{0}=\mathsf{B}.$$ Per tant, $\mathcal{S}$ admet infinites solucions.

– Marta Ribera Ramos.

Qüestió 1.6

Siga $\mathcal{S}$ un sistema lineal d’$m$ equacions amb $n$ incògnites sobre un cos $\mathbb{K}$. Demostra que si $\mathcal{S}$ és un sistema compatible determinat aleshores $m\ge n$.

Solució

Sense solució.

2. Espais vectorials

Qüestió 2.1

Defineix espai vectorial.

Solució

Donat un cos $\mathbb{K}$, un $\mathbb{K}$-espai vectorial és una estructura algebraica del tipus $(V,+,\cdot ,0)$, on

• $V$ és un conjunt, els elements del qual s’anomenen vectors.
• $0$ és un vector en $V$, que s’anomena vector zero.
• La suma, denotada $+$, és una operació binària del tipus $+:V\times V⟶V$ que satisfà les propietats associativa i commutativa, té al vector zero com a neutre i satisfà que tot vector té un oposat per a la suma. Es pot demostrar que, per a cada vector $v\in V$, el seu oposat és únic. El denotarem per $-v$. És a dir, per a tot $u,v,w\in V$ es té que $$\begin{array}{rl}u+(v+w)& =(u+v)+w;\\ u+v& =v+u;\\ 0+v& =v+0=v;\\ v+(-v)& =(-v)+v=0.\end{array}$$ Estes quatre lleis fan de $(V,+,0)$ un grup abelià.
• El producte per escalar, denotat per $\cdot$, és una operació del tipus $\cdot :\mathbb{K}\times V⟶V$ satisfent, per a tot $\alpha ,\beta \in \mathbb{K}$ i per a tot $u,v\in V$, les següents quatre lleis $$\begin{array}{rl}(\alpha +\beta )v& =\alpha v+\beta v;\\ \alpha (u+v)& =\alpha u+\alpha v;\\ \alpha (\beta v)& =(\alpha \beta )v;\\ 1v& =v.\end{array}$$

– Marta Ribera Ramos.

Qüestió 2.2

Defineix conjunt de vectors linealment independent. Dóna un exemple d’un conjunt de vectors linealment independent d’${\mathbb{R}}^3$ format per dos vectors. Emprant la definició, demostra que aquest conjunt és linealment independent.

Solució

Siga $V$ un $\mathbb{K}$-espai vectorial i $S\subseteq V$ un subconjunt.

Direm que $S$ és linealment independent si tota combinació lineal del tipus $${\lambda }_1{s}_1+{\lambda }_2{s}_2+\cdots +{\lambda }_n{s}_n=0,$$ amb $n\in \mathbb{N}$, ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n\in \mathbb{K}$ i $s_1,s_2,\cdots ,s_n\in S$, necessàriament implica que ${\lambda }_1={\lambda }_2=\cdots ={\lambda }_n=0.$

En ${\mathbb{R}}^3$ considerem el conjunt de vectors $S=\{(1,0,0),(0,1,0)\}$.

Anem a demostrar que $S$ és linealment independent.

Siga una combinació lineal del tipus $$\lambda (1,0,0)+\mu (0,1,0)=(0,0,0).$$ D’aquesta darrera igualtat concloem que $(\lambda ,\mu ,0)=(0,0,0).$

Així, necessàriament, $\lambda =\mu =0.$

Per tant, $S$ és un conjunt de dos vectors linealment independent.

– Marta Ribera Ramos.

Qüestió 2.3

Dóna un exemple de sistema generador que no siga base.

Solució

Considerem el subconjunt d’${\mathbb{R}}^3$ $$S=\{(1,0,0),(0,1,0),(0,0,1),(1,1,1)\}.$$ Notem que $S$ és sistema generador d’${\mathbb{R}}^3$ perquè tota tupla $(x,y,z)$ d’${\mathbb{R}}^3$ es pot escriure com a combinació lineal dels vectors en $S$, per exemple $$(x,y,z)=x(1,0,0)+y(0,1,0)+z(0,0,1)+0(1,1,1).$$ No obstant, $S$ no és base ja que $S$ no és linealment independent.

Notem que $$(1,0,0)+(0,1,0)+(0,0,1)-(1,1,1)=(0,0,0)$$ és una combinació lineal dels vectors en $S$ igualada a zero on no tots els escalars són zero.

– Marta Ribera Ramos.

Qüestió 2.4

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^2$ i es consideren paràmetres $a,b\in \mathbb{R}$. Demostra que el subconjunt d’${\mathbb{R}}^2$ següent és un subespai vectorial d’${\mathbb{R}}^2$ per a tota elecció dels paràmetres $a$ i $b$. Determina en funció dels paràmetres $a$ i $b$ la corresponent dimensió. $$W=\{(x,y)\in {\mathbb{R}}^2\mid ax+by=0\}.$$

Solució

Sense solució.

Qüestió 2.5

Siga $\mathsf{AX}=\mathsf{0}$ un sistema d’equacions lineals homogeni, amb $\mathsf{A}\in {\mathrm{M}}_n(\mathbb{K})$. Demostra que el conjunt de solucions del sistema és un subespai vectorial de ${\mathbb{K}}^n$.

Solució

Notem que $\mathsf{0}$ és una solució del sistema, ja que $\mathsf{A}\mathsf{0}=\mathsf{0}$.

Siguen ${\mathsf{X}}_1$ i ${\mathsf{X}}_2$ dues solucions del sistema i siguen $\alpha$ i $\beta$ escalars en $\mathbb{K}$.

Volem vore que $\alpha {\mathsf{X}}_1+\beta {\mathsf{X}}_2$ és solució del sistema.

En efecte $$\mathsf{A}(\alpha {\mathsf{X}}_1+\beta {\mathsf{X}}_2)=\alpha {\mathsf{AX}}_1+\beta {\mathsf{AX}}_2=\alpha \mathsf{0}+\beta \mathsf{0}=\mathsf{0}.$$

Per tant, el conjunt de solucions del sistema és un subespai vectorial.

Qüestió 2.6

Dóna un sistema generador d’${\mathbb{R}}^3$ que no siga base.

Solució

Mireu la solució de la qüestió 2.3.

– Marta Ribera Ramos.

Qüestió 2.7

Siga $V$ un $\mathbb{K}$-espai vectorial, $\mathcal{B}$ una base de $V$ i $W\le V$ un subespai vectorial. És cert que existeix un subconjunt ${\mathcal{B}}^{\prime }\subseteq \mathcal{B}$ de forma que ${\mathcal{B}}^{\prime }$ és base de $W$?

Solució

Sense solució.

Qüestió 2.8

Dóna un conjunt de vectors linealment independent d’${\mathbb{R}}^3$ que no siga base.

Solució

Considerem el conjunt $S=\{(1,0,0),(0,1,0)\}$.

En la solució de la Qüestió 2.2 s’ha demostrat que és un conjunt de vectors linealment independent.

No és base perquè no és maximal per a la condició de ser linealment independent.

Notem que $S$ està inclós estrictament en la base canònica, $S\subset {\mathcal{B}}_{\mathrm{c}}^{(3)}$, i ${\mathcal{B}}_{\mathrm{c}}^{(3)}$ és linealment independent.

– Marta Ribera Ramos.

Qüestió 2.9

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^2$ i els següents subconjunts $$\begin{array}{rl}S& =\{(x,y)\in {\mathbb{R}}^2\mid x^2+y^2=1\};\\ T& =\{(x,y)\in {\mathbb{R}}^2\mid x>100,y>100\}.\end{array}$$ És cert que $S$ i $T$ són subespais vectorials de ${\mathbb{R}}^2$? Dóna bases per a $⟨S⟩$ i $⟨T⟩$.

Solució

Sense solució.

Qüestió 2.10

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen $U,W\le V$. Demostra que les següents afirmacions són equivalents.

1. La suma és directa, és a dir, $U\oplus W$;
2. Per a tot $u\in U$ i per a tot $w\in W$, si $u+w=0$, aleshores $u=w=0$;
3. Tot vector $v\in U+W$ s’escriu de forma única.

Solució

Sense solució.

Qüestió 2.11

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen $S,T\subseteq V$ subconjunts de $V$. Raona sobre la veritat o falsedat de les següents afirmacions.

• Si $S$ i $T$ són linealment independents, aleshores $S\cup T$ és linealment independent.
• Si $S$ i $T$ són linealment independents, aleshores $S\cap T$ és linealment independent.

Solució

Sense solució.

Qüestió 2.12

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen $S,T\subseteq V$ subconjunts de $V$. Raona sobre la veritat o falsedat de les següents afirmacions.

• Si $S$ i $T$ són sistemes generadors, aleshores $S\cup T$ és sistema generador.
• Si $S$ i $T$ són sistemes generadors, aleshores $S\cap T$ és sistema generador.

Solució

Sense solució.

Qüestió 2.13

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen $U,W\le V$ subespais vectorials. Siguen ${\mathcal{B}}_U$ i ${\mathcal{B}}_W$ bases d’$U$ i $W$, respectivament, tals que ${\mathcal{B}}_U\cap {\mathcal{B}}_W=\varnothing$. Demostra que si ${\mathcal{B}}_U\cup {\mathcal{B}}_W$ és base de $V$, aleshores $V=U\oplus W$.

Solució

Sense solució.

Qüestió 2.14

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $n$ i siga $W\le V$ un subespai vectorial de $V$ de dimensió $n-1$. Raona sobre la veritat o falsedat de les següents afirmacions

• Si $S\subseteq V$ és un subconjunt de $V$ que conté a $W$ estrictament, és a dir $W\subset S\subseteq V$, aleshores $S=V$.
• Si $U\le V$ és un subespai vectorial de $V$ que conté a $W$ estrictament, és a dir $W\subset U\subseteq V$, aleshores $U=V$.

Solució

Sense solució.

Qüestió 2.15

Siga $V$ un $\mathbb{K}$-espai vectorial finitament generat. Demostra que si $\{v,w\}\subseteq V$ és un conjunt de vectors linealment independent, aleshores ${\dim }_{\mathbb{K}}(V)\ge 2$.

Solució

Sense solució.

Qüestió 2.16

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^2$. Determina si el següent subconjunt de vectors és un subespai vectorial $$W=\{(x,1)\in {\mathbb{R}}^2\mid x\in \mathbb{R}\}.$$

Solució

Sense solució.

Qüestió 2.17

Siga $\mathbb{K}$ un cos i siguen natural $m,n\in \mathbb{N}$. Determina bases per als $\mathbb{K}$-espais vectorials

1. ${\mathbb{K}}^n;$
2. ${\mathrm{M}}_{mn}(\mathbb{K});$
3. ${\mathbb{K}}_{\le n}[x].$

Solució

Sense solució.

Qüestió 2.18

Demostra que si $V$ és un $\mathbb{K}$-espai vectorial i $U\le V$ és un subespai vectorial, aleshores $0\in U$.

Solució

Sense solució.

Qüestió 2.19

Defineix conjunt de vectors linealment independent maximal.

Solució

Sense solució.

Qüestió 2.20

Sobre l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^3$ es considera el subespai vectorial $U=⟨(1,1,1),(1,2,3)⟩\le {\mathbb{R}}^3$. Troba, si és possible, un subespai vectorial $W\le {\mathbb{R}}^3$ de dimensió $1$ tal que ${\mathbb{R}}^3=U+W$.

Solució

Sense solució.

Qüestió 2.21

Troba tots els subespais vectorials d’${\mathbb{R}}^2$ que continguen els vectors $(1,1)$ i $(0,1)$.

Solució

Sense solució.

Qüestió 2.22

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $3$. Demostra que, per a tot $1\le i\le 3$, existeixen subconjunts $S_i\le V$ tals que $|S_i|=i$, ${\dim }_{\mathbb{K}}⟨S_i⟩=i$ de forma que $S_1\subseteq S_2\subseteq S_3$.

Solució

Sense solució.

Qüestió 2.23

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen subconjunts $S\subseteq T\subseteq V$. Demostra que si $S$ és sistema generador, aleshores $T$ és sistema generador.

Solució

Sense solució.

Qüestió 2.24

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $\mathcal{B}=\{e_1,\cdots ,e_n\}$ una base de $V$. Demostra que $\mathcal{B}$ és un conjunt de vectors linealment independent maximal.

Solució

Sense solució.

Qüestió 2.25

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $U\le V$ un subespai vectorial. Demostra que existeix un subespai vectorial $W\le V$ tal que $V=U\oplus W$.

Solució

Sense solució.

Qüestió 2.26

Dóna un exemple de sistema generado d’${\mathbb{R}}^3$ que no siga base. Demostra que és sistema generador i que no és base.

Solució

Sense solució.

Qüestió 2.27

Siga $V$ un $\mathbb{K}$-espai vectorial i $G\subseteq V$ un sistema generador. És cert que qualsevol vector de $V$ pot escriure’s de forma única com a combinació lineal dels vectors en $G$? Justifica la resposta.

Solució

Sense solució.

Qüestió 2.28

Siga $V$ un $\mathbb{K}$-espai vectorial i $S,T{\subseteq }_{\mathrm{f}}V$ subconjunts finits de $V$ tals que $S\cup T$ és linealment independent i $S\cap T=\varnothing$. És cert que $⟨S⟩\cap ⟨T⟩=\{0\}$?

Solució

Sense solució.

Qüestió 2.29

Sobre l’$\mathbb{R}$-espai ${\mathbb{R}}^2$ es consideren els subconjunts següents $$\begin{array}{rl}S& =\{(x,y)\in {\mathbb{R}}^2\mid x+y=1\};\\ T& =\{(x,y)\in {\mathbb{R}}^2\mid x+y=0\}.\end{array}$$ Determina bases per a $⟨S⟩$ i $⟨T⟩$.

Solució

Sense solució.

Qüestió 2.30

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $n\in \mathbb{N}$. Siga $\{e_1,\cdots ,e_n\}$ una base de $V$ i siga $\{e_1,{\bar{e}}_1\}$ un conjunt de vectors linealment independent en $V$. És cert que el conjunt $\{{\bar{e}}_1,e_2,\cdots ,e_n\}$ és una base de $V$?

Solució

Sense solució.

Qüestió 2.31

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $n\in \mathbb{N}$. Demostra que, si $v\in V-\{0\}$, aleshores existeix un subespai vectorial $W\le V$ de dimensió $n-1$ tal que $V=⟨v⟩\oplus W$.

Solució

Sense solució.

Qüestió 2.32

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen $W,U\le V$ subespais vectorials de $V$. Demostra que $⟨W\cup U⟩=W+U$.

Solució

Sense solució.

Qüestió 2.33

És cert que tot sistema generador d’${\mathbb{R}}^3$ és base? Justifica la resposta.

Solució

Sense solució.

Qüestió 2.34

Troba subespais $W,U\le {\mathbb{R}}^2$ tals que ${\mathbb{R}}^2=W\oplus U$.

Solució

Sense solució.

Qüestió 2.35

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^2$ i una base $\mathcal{B}=\{e_1,e_2\}$ d’ ${\mathbb{R}}^2$. Es considera la matriu $$\mathsf{A}=\left[\begin{array}{cc}1& -1\\ 2& 0\end{array}\right]\in {\mathrm{M}}_2(\mathbb{R})$$ Determina

1. Una base $\bar{\mathcal{B}}$ d’ ${\mathbb{R}}^2$ per a la qual $\mathsf{A}$ és la matriu canvi de base de $\mathcal{B}$ a $\bar{\mathcal{B}}$.
2. Una base $\bar{\mathcal{B}}$ d’ ${\mathbb{R}}^2$ per a la qual $\mathsf{A}$ és la matriu canvi de base de $\bar{\mathcal{B}}$ a $\mathcal{B}$.

Solució

Sense solució.

Qüestió 2.36

Siga $V$ un $\mathbb{K}$-espai vectorial finitament generat. Defineix dimensió de $V$. Què garantitza que aquesta definició tinga sentit?

Solució

Sense solució.

Qüestió 2.37

Demostra que els següents conjunts són base d’${\mathbb{R}}^3$. $$\begin{array}{rl}\mathcal{B}& =\{(-1,2,1),(1,0,1),(0,1,0)\};\\ \bar{\mathcal{B}}& =\{(1,0,0),(0,0,1),(0,1,1)\}.\end{array}$$ Determina la matriu canvi de base de $\mathcal{B}$ a $\bar{\mathcal{B}}$.

Solució

Sense solució.

Qüestió 2.38

És cert que si $U$ i $W$ són subespais vectorials d’ ${\mathbb{R}}^2$ no nuls i distints entre sí, aleshores ${\mathbb{R}}^2=U+W$? Justifica la reposta.

Solució

Sense solució.

Qüestió 2.39

Siga $p\in \mathbb{P}$ un nombre primer i $n\in \mathbb{N}$. Siga $V$ un ${\mathbb{Z}}_p$-espai vectorial de dimensió $n$. Determina $\mid V\mid$.

(Ajuda: ${\mathbb{Z}}_p$ és un cos amb $p$ elements.)

Solució

Sense solució.

Qüestió 2.40

Per a l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^2$ es consideren les bases ${\mathcal{B}}_1=\{(1,0),(1,1)\}$ i ${\mathcal{B}}_2=\{(2,1),(1,2)\}$. Calcula les coordenades en la base ${\mathcal{B}}_2$ del vector que té coordenades ${\mathsf{X}}_1$ en la base ${\mathcal{B}}_1$, on $${\mathsf{X}}_1=\left[\begin{array}{c}1\\ 1\end{array}\right]\in {\mathrm{M}}_{2,1}(\mathbb{R})$$

Solució

Sense solució.

Qüestió 2.41

Siga $W\le {\mathbb{R}}^2$ tal que $(1,1)\in W$ i tal que $W\ne {\mathbb{R}}^2$. És cert que $(0,1)\in W$? Justifica la resposta.

Solució

Sense solució.

Qüestió 2.42

Troba tots els subespais $W$ d’ ${\mathbb{R}}^2$ tals que $(1,1)$ i $(1,0)$ pertanyen a $W$.

Solució

Sense solució.

Qüestió 2.43

Per a l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^2$ es consideren les bases $$\begin{array}{rl}{\mathcal{B}}_1& =\{(1,0),(1,1)\};\\ {\mathcal{B}}_2& =\{(2,1),(1,2)\}.\end{array}$$ Pots trobar un vector que tinga les mateixes coordenades respecte a ${\mathcal{B}}_1$ i a ${\mathcal{B}}_2$?

Solució

Sense solució.

Qüestió 2.44

Siga $V$ un $\mathbb{K}$-espai vectorial, $n\in \mathbb{N}$, $v_1,\cdots ,v_n$ vectors en $V$ i ${\lambda }_1,\cdots ,{\lambda }_n,{\mu }_1,\cdots ,{\mu }_n$ escalars en $\mathbb{K}$. És cert que si $${\lambda }_1{v}_1+\cdots +{\lambda }_n{v}_n={\mu }_1{v}_1+\cdots +{\mu }_n{v}_n$$ aleshores ${\lambda }_i={\mu }_i$, per a tot $1\le i\le n$?

Solució

Sense solució.

Qüestió 2.45

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen $U,W\le V$. Siguen $S,T\subseteq V$ sistemes generadors d’ $U$ i de $W$, respectivament. És cert que $S\cup T$ és sistema generador per a $U+W$?

Solució

Sense solució.

Qüestió 2.46

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $U\le V$. Demostra que existeix un subespai $W\le V$ tal que $V=U\oplus W$.

Solució

Sense solució.

Qüestió 2.47

Es considera l’ $\mathbb{R}$-espai vectorial ${\mathbb{R}}^4$ i el subespai $U\le {\mathbb{R}}^4$ donat per $$U=⟨(1,1,1,1),(1,2,3,4)⟩.$$ Troba raonadament un subespai vectorial $W\le {\mathbb{R}}^4$ de forma que ${\mathbb{R}}^4=U\oplus W$.

Solució

Sense solució.

Qüestió 2.48

Siga $V$ un $\mathbb{K}$-espai vectorial. Siga $S=\{v_1,\cdots ,v_n\}\subseteq V$ tal que tot vector de $V$ pot escriure’s de forma única com a combinació lineal dels vectors d’ $S$. És cert que $S$ és una base de $V$?

Solució

Sense solució.

Qüestió 2.49

Siga $V$ un $\mathbb{K}$-espai vectorial i $U,W\le V$ tals que $V=U+W$. Siga $v\in V-U$. És cert que $v\in W$?

Solució

Sense solució.

Qüestió 2.50

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $W\le V$ un subespai vectorial. Siga ${\mathcal{B}}_W$ una base de $W$ i $v$ un vector en $V-W$. Demostra que ${\mathcal{B}}_W\cup \{v\}$ és linealment independent.

Solució

Sense solució.

Qüestió 2.51

Es considera $\mathbb{R}[x]$, l’$\mathbb{R}$-espai vectorial de polinomis amb indeterminada $x$ i coeficients en $\mathbb{R}$. Es considera $p(x)$ un polinomi en $\mathbb{R}[x]$ de grau $k\in \mathbb{N}$ amb $k\ge 1$. Es consideren els següents subconjunts $$U=\{q(x)\in \mathbb{R}[x]\mid p(x)\mid q(x)\};W={\mathbb{R}}_{\le k-1}[x].$$ Demostra que 1. $U$ i $W$ són subespais vectorials d’$\mathbb{R}[x]$; 2. $\mathbb{R}[x]=U\oplus W$. Pots emprar la Divisió Euclidiana per als polinomis en $\mathbb{R}[x]$.

Solució

Sense solució.

Qüestió 2.52

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^4$ i els següents subespais vectorials $$\begin{array}{rl}{W}_1& =\{(x,y,z,t)\in {\mathbb{R}}^4|\begin{array}{rcl}x+2y& =& 0\\ x+2z-t& =& 0\\ -y+t& =& 0\end{array}\};\\ W_2& =\{(x,y,z,t)\in {\mathbb{R}}^4|\begin{array}{rcl}-2x-y+t& =& 0\\ 2z-t& =& 0\\ -y+t& =& 0\end{array}\};\\ W_3& =⟨(1,2,-1,0),(0,1,3,2),(-1,-1,4,2)⟩.\end{array}$$

1. Determina una base per a cada subespai.
2. Determina una base per a $W_1\cap W_2\cap W_3$.
3. Determina una base per a $W_1+W_2+W_3$.

Solució

Sense solució.

Qüestió 2.53

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^3$ i els subespais vectorials $U$ i $W$, on $$\begin{array}{rl}U& =\{(x,y,z)\in {\mathbb{R}}^3|\begin{array}{ccccc}2x& +& y& =& 0\\ y& -& z& =& 0\end{array}\};\\ W& =⟨(1,0,1),(-1,1,0)⟩.\end{array}$$ Determina ${\dim }_{\mathbb{R}}(U)$, ${\dim }_{\mathbb{R}}(W)$ i ${\dim }_{\mathbb{R}}(U\cap W)$.

Solució

Sense solució.

Qüestió 2.54

Siga $V$ un $\mathbb{K}$-espai vectorial i $\{W_i\le V\mid i\in I\}$ una família de subespais vectorials en $V$. Demostra que les següents afirmacions són equivalents

1. $\underset{i\in I}{⨁}{W}_i$ (la suma és directa);
2. $\mathrm{\forall }F{\subseteq }_{\mathrm{f}}I$, $\mathrm{\forall }(w_i{)}_{i\in F}\in \prod _{i\in F}{W}_i$, si $\sum _{i\in F}{w}_i=0$, aleshores, $\mathrm{\forall }i\in F$, $w_i=0$;
3. Tot element no nul de $\sum _{i\in I}{W}_i$ s’escriu de forma única. \end{itemize}

Solució

Sense solució.

Qüestió 2.55

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $\mathcal{B}=\{e_1,\cdots ,e_n\}$ una base de $V$. Demostra que $$V=⟨e_1⟩\oplus \cdots \oplus ⟨e_n⟩.$$

Solució

Sense solució.

Qüestió 2.56

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^3$. Troba una base del subespai vectorial $W$, on $$W=\{(x,y,z)\in {\mathbb{R}}^3|\begin{array}{ccccccc}x& +& 2y& +& z& =& 0\\ 2x& +& 3y& +& z& =& 0\end{array}\}.$$

Solució

Sense solució.

Qüestió 2.57

Siga $V$ un $\mathbb{K}$-espai vectorial i siguen $S,T\subseteq V$ subconjunts de vectors en $V$. Demostra que els següents conjunts són iguals.

1. $⟨S\cup T⟩;$
2. $⟨S⟩+⟨T⟩;$
3. $⟨⟨S⟩\cup ⟨T⟩⟩.$

Solució

Sense solució.

Qüestió 2.58

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}_{\le 3}[x]$ de polinomis d’indeterminada $x$ amb coeficients reals i grau fitat per $3$. Demostra que el conjunt de polinomis $\{x^3+2x,x^3+x^2,x^3+2\}$ és linealment independent. Amplia aquest conjunt fins a obtindre una base de ${\mathbb{R}}_{\le 3}[x]$.

Solució

Sense solució.

Qüestió 2.59

Es considera l’$\mathbb{R}$-espai vectorial estàndard ${\mathbb{R}}^3$. Determina tres subespais vectorials $W_1,W_2,W_3\le {\mathbb{R}}^3$ amb $W_2\ne W_3$ per als quals $$W_1\oplus W_2={\mathbb{R}}^3=W_1\oplus W_3.$$ Existeix algun subespai vectorial $W\le {\mathbb{R}}^3$ que tinga un espai complementari unívocament determinat?

Solució

Sense solució.

3. Aplicacions lineals

Qüestió 3.1

Dóna la definició d’aplicació lineal.

Solució

Donats dos $\mathbb{K}$-espais vectorials $V$ i $W$, una aplicació $f:V⟶W$ és una aplicació lineal si, per a tot parell de vectors $u,v\in V$ i per a tot parell d’escalars $\alpha ,\beta \in \mathbb{K}$ es té que $$f(\alpha v+\beta u)=\alpha f(v)+\beta f(u).$$

– Marta Ribera Ramos.

Qüestió 3.2

Es considera l’aplicació lineal $$\begin{array}{rccl}f:& {\mathbb{R}}^2& ⟶& {\mathbb{R}}^3\\ & (x,y)& ⟼& (x+y,y,2x)\end{array}$$ Es consideren ${\mathcal{B}}_2=\{e_1,e_2\}$ i ${\mathcal{B}}_3=\{(0,1,0),(0,0,-1),(2,0,0)\}$, la base canònica d’${\mathbb{R}}^2$ i una base d’${\mathbb{R}}^3$, respectivament. Determina la matriu coordenada d’$f$ de ${\mathcal{B}}_2$ a ${\mathcal{B}}_3$.

Solució

Notem que $$\begin{array}{rl}f(1,0)& =(1,0,2)=0(0,1,0)+(-2)(0,0,-1)+\frac{1}{2}(2,0,0);\\ f(0,1)& =(1,1,0)=1(0,1,0)+0(0,0,-1)+\frac{1}{2}(2,0,0).\end{array}$$

Per tant, la matriu coordenada d’$f$ de ${\mathcal{B}}_2$ a ${\mathcal{B}}_3$ és $$\left[\begin{array}{cc}0& 1\\ -2& 0\\ \frac{1}{2}& \frac{1}{2}\end{array}\right]$$

– Marta Ribera Ramos.

Qüestió 3.3

Troba l’expressió analítica d’una aplicació lineal $f:{\mathbb{R}}^3⟶{\mathbb{R}}^3$ que satisfaça $\mathrm{Ker}(f)=⟨(1,1,1)⟩$.

Solució

Considerem una base d’${\mathbb{R}}^3$ que continga la tupla $(1,1,1)$, per exemple $$\mathcal{B}=\{(1,0,0),(0,1,0),(1,1,1)\}$$ Notem que $\mathcal{B}$ és base d’${\mathbb{R}}^3$ perquè $|\mathcal{B}|=3={\dim }_{\mathbb{R}}({\mathbb{R}}^3)$ i, a més, $\mathcal{B}$ és sistema generador d’${\mathbb{R}}^3$. En efecte, si $(x,y,z)\in {\mathbb{R}}^3$, aleshores $$(x,y,z)=(x-z)(1,0,0)+(y-z)(0,1,0)+z(1,1,1).$$

Considerem l’aplicació $$\begin{array}{rccl}h:& \mathcal{B}& ⟶& {\mathbb{R}}^3\\ & (1,0,0)& ⟼& (1,0,0)\\ & (0,1,0)& ⟼& (0,1,0)\\ & (1,1,1)& ⟼& (0,0,0)\end{array}$$

Per Propietat Universal, existeix una única aplicació lineal $h^{\mathrm{♯}}:{\mathbb{R}}^3⟶{\mathbb{R}}^3$ satisfent que $h^{\mathrm{♯}}\circ {\mathrm{in}}_{\mathcal{B}}=h$. De fet, podem obtindre la seua expressió analítica com segueix $$h^{\mathrm{♯}}(x,y,z)=(x-z)h(1,0,0)+(y-z)h(0,1,0)+(z)h(1,1,1)=(x-z,y-z,0).$$

Notem que $$\mathrm{Ker}(h^{\mathrm{♯}})=\{(x,y,z)\in {\mathbb{R}}^3|\begin{array}{c}x-z=0\\ y-z=0\end{array}\}=⟨(1,1,1)⟩.$$ – Marta Ribera Ramos.

Qüestió 3.4

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials finitament generats. Demostra que $V_1$ és isomorf a $V_2$ si, i només si, ${\dim }_{\mathbb{K}}(V_1)={\dim }_{\mathbb{K}}(V_2)$.

Solució

Suposem que $V_1$ és isomorf a $V_2$. Siga $f:V_1⟶V_2$ un isomorfisme. Siga ${\mathcal{B}}_1$ una base de $V_1$. Aleshores sabem que $f[{\mathcal{B}}_1]$ és base de $V_2$. Notem la següent cadena d’igualtats $$\begin{array}{}\text{(}{\mathcal{B}}_1\text{ és base de }{V}_1\text{)}& {\dim }_{\mathbb{K}}(V_1)& =|{\mathcal{B}}_1|\text{(}f\text{ és injectiva)}& & =|f[{\mathcal{B}}_1]|\text{(}f[{\mathcal{B}}_1]\text{ és base de }{V}_2\text{)}& & ={\dim }_{\mathbb{K}}(V_2).\end{array}$$

Per tant, ${\dim }_{\mathbb{K}}(V_1)={\dim }_{\mathbb{K}}(V_2)$.

Suposem ara que ${\dim }_{\mathbb{K}}(V_1)={\dim }_{\mathbb{K}}(V_2)$. Com $V_1$ i $V_2$ són finitament generats, siga $n\in \mathbb{N}$ per al què ${\dim }_{\mathbb{K}}(V_1)=n$. Siguen ${\mathcal{B}}_1=\{e_1,\cdots ,e_n\}$ i ${\mathcal{B}}_2=\{d_1,\cdots ,d_n\}$ bases de $V_1$ i $V_2$, respectivament.

Considerem l’aplicació $$\begin{array}{rccl}h:& {\mathcal{B}}_1& ⟶& V_2\\ & e_i& ⟼& d_i\end{array}$$

Per Propietat Universal, existeix una única aplicació lineal $h^{\mathrm{♯}}:V_1⟶V_2$ satisfent que $h^{\mathrm{♯}}\circ {\mathrm{in}}_{{\mathcal{B}}_1}=h$. Notem que aquesta aplicació lineal satisfà que $$\begin{array}{rl}{h}^{\mathrm{♯}}[{\mathcal{B}}_1]& =h^{\mathrm{♯}}[\{e_1,\cdots ,e_n\}]\\ & =\{h^{\mathrm{♯}}(e_1),\cdots ,h^{\mathrm{♯}}(e_n)\}\\ \text{(}{h}^{\mathrm{♯}}\circ {\mathrm{in}}_{{\mathcal{B}}_1}=h\text{)}& & =\{h(e_1),\cdots ,h(e_n)\}& =\{d_1,\cdots ,d_n\}\\ & ={\mathcal{B}}_2.\end{array}$$

Per tant, com $h^{\mathrm{♯}}$ és una aplicació lineal de $V_1$ en $V_2$ que transforma una base de $V_1$ en una base de $V_2$, podem afirmar que $h^{\mathrm{♯}}$ és un isomorfisme de $V_1$ a $V_2$, és a dir, $V_1$ és isomorf a $V_2$.

– Marta Ribera Ramos.

Qüestió 3.5

Es consideren els $\mathbb{R}$-espais vectorials ${\mathbb{R}}^3$ i ${\mathbb{R}}^2$. Determina en cadascun dels cassos, si és possible, l’existència d’una aplicació lineal $f:{\mathbb{R}}^3⟶{\mathbb{R}}^2$ tal que

1. $f(1,0,1)=(2,1)$; $f(1,0,0)=(2,2)$; $f(0,0,2)=(1,0)$;
2. $f(1,0,1)=(2,1)$; $f(1,0,0)=(2,2)$; $f(2,0,1)=(1,0)$.

Solució

En el primer cas no és possible trobar aquesta aplicació lineal. Pel contrarecíproc, si suposem que existira una aplicació lineal $f:{\mathbb{R}}^3⟶{\mathbb{R}}^2$ satisfent les condicions descrites en el cas 1., aleshores s’hauria de complir que $$\begin{array}{rl}f(1,0,1)& =f(1(1,0,0)+\frac{1}{2}(0,0,2))\\ \text{(}f\text{ és lineal)}& & =1f(1,0,0)+\frac{1}{2}f(0,0,2)\text{(}f(1,0,0)=(2,2)\text{)}& & =1(2,2)+\frac{1}{2}f(0,0,2)\text{(}f(0,0,2)=(1,0)\text{)}& & =1(2,2)+\frac{1}{2}(1,0)& =(\frac{5}{2},2).\end{array}$$

La darrera igualtat és incompatible amb que $f(1,0,1)=(2,1)$.

En el segon cas ens trobem en les mateixes circumstàncies. Pel contrarecíproc, si suposem que existira una aplicació lineal $f:{\mathbb{R}}^3⟶{\mathbb{R}}^2$ satisfent les condicions descrites en el cas 2., aleshores s’hauria de complir que $$\begin{array}{rl}f(1,0,1)& =f(-1(1,0,0)+(2,0,1))\\ \text{(}f\text{ és lineal)}& & =-f(1,0,0)+f(0,0,2)\text{(}f(1,0,0)=(2,2)\text{)}& & =-1(2,2)+f(0,0,2)\text{(}f(0,0,2)=(1,0)\text{)}& & =-1(2,2)+(1,0)& =(-1,-2).\end{array}$$

La darrera igualtat és incompatible amb que $f(1,0,1)=(3,1)$.

– Marta Ribera Ramos.

Qüestió 3.6

Defineix matriu coordenada d’una aplicació lineal.

Solució

Siguen $V$ i $W$ dos $\mathbb{K}$-espais vectorials i siga $f:V⟶W$ una aplicació lineal. Siguen ${\mathcal{B}}_V=\{e_1,\cdots ,e_n\}$ i ${\mathcal{B}}_W=\{d_1,\cdots ,d_m\}$ bases de $V$ i $W$, respectivament. Es defineix la com a la matriu $\mathsf{A}\in {\mathrm{M}}_{mn}(\mathbb{K})$ que té, per a cada $1\le j\le n$, com a columna $j$-èssima les coordenades de $f(e_j)$ en la base ${\mathcal{B}}_W$.

– Marta Ribera Ramos.

Qüestió 3.7

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $f:V⟶V$ una aplicació lineal tal que $\mathrm{Im}(f)\subseteq \mathrm{Ker}(f)$. És cert que $f=0$?

Solució

La resposta és No, $f$ no ha de ser necessàriament l’aplicació nul·la. Donem un contraexemple. En ${\mathbb{R}}^2$, considerem l’aplicació lineal $$\begin{array}{rccl}f:& {\mathbb{R}}^2& ⟶& {\mathbb{R}}^2\\ & (x,y)& ⟼& (y,0).\end{array}$$

Notem que $$\begin{array}{rl}\mathrm{Ker}(f)& =\{(x,y)\in {\mathbb{R}}^2\mid y=0\};\\ \mathrm{Im}(f)& =\{(x,y)\in {\mathbb{R}}^2\mid y=0\}.\end{array}$$

Per tant, $\mathrm{Im}(f)\subseteq \mathrm{Ker}(f)$. De fet, en aquest cas concret, els dos subespais vectorials, $\mathrm{Im}(f)$ i $\mathrm{Ker}(f)$ són iguals. Però no es té que $f=0$, ja que $f(0,1)=(1,0)\ne (0,0)$.

– Marta Ribera Ramos.

Qüestió 3.8

Dóna un isomorfisme explícit entre els $\mathbb{R}$-espais vectorials ${\mathrm{M}}_2(\mathbb{R})$ i ${\mathbb{R}}_{\le 3}[x]$.

Solució

Sense solució.

Qüestió 3.9

Es considera l’ $\mathbb{R}$-espai vectorial ${\mathbb{R}}^2$ i la seua base canònica ${\mathcal{B}}_{\mathrm{c}}$. Siga $f:{\mathbb{R}}^2⟶{\mathbb{R}}^2$ l’aplicació lineal que té com a matriu coordenada de la base ${\mathcal{B}}_{\mathrm{c}}$ a la base ${\mathcal{B}}_{\mathrm{c}}$ a la matriu $$\mathsf{A}=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]$$ Determina una base $\bar{\mathcal{B}}$ d’ ${\mathbb{R}}^2$ per a la qual la matriu coordenada d’ $f$ de la base $\bar{\mathcal{B}}$ a la base ${\mathcal{B}}_{\mathrm{c}}$ és la matriu identitat de tamany $2$, és a dir ${\mathsf{I}}_2$.

Solució

Sense solució.

Qüestió 3.10

Es consideren els $\mathbb{K}$-espais vectorials $V_1$ i $V_2$ amb ${\dim }_{\mathbb{K}}(V_1)=2$ i ${\dim }_{\mathbb{K}}(V_2)=3$. Es consideren les bases ${\mathcal{B}}_1=\{e_1,e_2\}$ i ${\mathcal{B}}_2=\{d_1,d_2,d_3\}$ de $V_1$ i $V_2$, respectivament. Es considera l’aplicació lineal $f:V_1⟶V_2$ que té a $\mathsf{A}$ com a matriu coordenada d’ $f$ de ${\mathcal{B}}_1$ a ${\mathcal{B}}_2$, on $$\mathsf{A}=\left[\begin{array}{cc}1& 2\\ 0& -1\\ 1& 1\end{array}\right]$$ Determina

1. Una base per a $\mathrm{Ker}(f)$;
2. Una base per a $\mathrm{Im}(f)$.

Solució

Sense solució.

Qüestió 3.11

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials i siga $f:V_1⟶V_2$ una aplicació lineal. Siga $U_1\le V_1$ un subespai vectorial. Demostra que $f[U_1]\le V_2$.

Solució

Sense solució.

Qüestió 3.12

Es considera l’aplicació transposada $$\begin{array}{rccl}(\cdot {)}^{\mathsf{t}}:& {\mathrm{M}}_{mn}(\mathbb{K})& ⟶& {\mathrm{M}}_{nm}(\mathbb{K})\\ & \mathsf{A}& ⟼& {\mathsf{A}}^{\mathsf{t}}.\end{array}$$ Demostra que l’aplicació transposada és un isomofisme de $\mathbb{K}$-espais vectorials.

Solució

Sense solució.

Qüestió 3.13

Siga $V$ un $\mathbb{K}$-espai vectorial i $\mathcal{B}=\{v_1,v_2\}$ una base de $V$. Siga $f:V⟶V$ una aplicació lineal bijectiva. Troba raonadament una base $\bar{\mathcal{B}}$ de $V$ de manera que la matriu coordenada d’$f$ de $\mathcal{B}$ a $\bar{\mathcal{B}}$ siga la matriu identitat ${\mathsf{I}}_2$.

Solució

Sense solució.

Qüestió 3.14

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials i siga $f:V_1⟶V_2$ una aplicació lineal. Siga $\{v_1,\cdots ,v_n\}$ un conjunt de vectors en $V_1$ linealment independent. És cert que si $f$ és injectiva, aleshores $\{f(v_1),\cdots ,f(v_n)\}$ és linealment independent?

Solució

Sense solució.

Qüestió 3.15

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials i siga $f:V_1⟶V_2$ una aplicació lineal. Siguen $v_1,\cdots ,v_n$ vectors en $V_1$. És cert que si $\{f(v_1),\cdots ,f(v_n)\}$ és linealment independent, aleshores $\{v_1,\cdots ,v_n\}$ és linealment independent?

Solució

Sense solució.

Qüestió 3.16

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials i siga $f:V_1⟶V_2$ una aplicació lineal. Siguen $v_1,\cdots ,v_n$ vectors en $V_1$. És cert que si $\{v_1,\cdots ,v_n\}$ és linealment independent, aleshores $\{f(v_1),\cdots ,f(v_n)\}$ és linealment independent?

Solució

Sense solució.

Qüestió 3.17

Es considera l’aplicació lineal $$\begin{array}{rccl}f:& {\mathbb{R}}^3& ⟶& {\mathbb{R}}^2\\ & (x,y,z)& ⟼& (x+y,-z)\end{array}$$ Per als subespais vectorials $$\begin{array}{rl}W& =\{(x,y,z)\in {\mathbb{R}}^3\mid x+y=0\}\le {\mathbb{R}}^3;\\ U& =\{(x,y)\in {\mathbb{R}}^2\mid 2x+y=0\}\le {\mathbb{R}}^2.\end{array}$$ Determina una base per a $f[W]$ i una base per a $f^{-1}[U]$.

Solució

Sense solució.

Qüestió 3.18

Siga $\mathcal{B}=\{e_1,e_2,e_3\}$ una base d’ ${\mathbb{R}}^3$ i siga $f\in {\mathrm{End}}_{\mathbb{R}}({\mathbb{R}}^3)$ tal que $$f(e_1)=-e_1;f(e_2)=e_2+e_1;f(e_3)=e_2-e_3.$$ Suposem que la matriu canvi de base de $\mathcal{B}$ a la base canònica és $$\mathsf{A}=\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 1\\ 0& 1& 0\end{array}\right]$$ Determina

1. La matriu coordenada d’ $f$ de la base $\mathcal{B}$ a la base $\mathcal{B}$;
2. La matriu coordenada d’ $f$ de la base $\mathcal{B}$ a la base canònica;
3. Una base de $\mathrm{Ker}(f)$;
4. La dimensió d’ $\mathrm{Im}(f)$.

Solució

Sense solució.

Qüestió 3.19

Determina un endomorfisme $f:{\mathbb{R}}^3⟶{\mathbb{R}}^3$ tal que

1. $\mathrm{Ker}(f)=\{(x,y,z)\in {\mathbb{R}}^3\mid x-2y=0;x+z=0\}$;
2. $\mathrm{Im}(f)=⟨(1,0,1),(1,0,0)⟩$.

Solució

Sense solució.

Qüestió 3.20

Es consideren els $\mathbb{R}$-espais vectorials ${\mathbb{R}}^3$ i ${\mathbb{R}}^2$ amb les bases respectives $$\begin{array}{rl}{\mathcal{B}}_3& =\{(1,0,-1),(0,2,1),(1,0,0)\};\\ {\mathcal{B}}_2& =\{(0,1),(1,1)\}.\end{array}$$ Es considera l’aplicació lineal $f:{\mathbb{R}}^3⟶{\mathbb{R}}^2$ que té com a matriu coordenada de ${\mathcal{B}}_3$ a ${\mathcal{B}}_2$ a la matriu $$\mathsf{A}=\left[\begin{array}{ccc}1& 0& 1\\ -1& -1& -2\end{array}\right]$$ Determina la matriu coordenada d’$f$ en les respectives bases canòniques.

Solució

Sense solució.

Qüestió 3.21

Es consideren els $\mathbb{R}$-espais vectorials ${\mathbb{R}}^3$ i $\mathbb{R}$ amb les bases respectives $${\mathcal{B}}_3=\{(0,0,-1),(0,2,1),(1,0,0)\};{\mathcal{B}}_1=\{2\}.$$ Es considera l’aplicació lineal $f:{\mathbb{R}}^3⟶\mathbb{R}$ que té com a matriu coordenada de ${\mathcal{B}}_3$ a ${\mathcal{B}}_1$ a la matriu $$\mathsf{A}=\left[\begin{array}{ccc}-1& 0& 0\end{array}\right]$$ Determina l’expressió analítica d’$f$.

Solució

Sense solució.

Qüestió 3.22

Raona l’existència d’un endomorfisme $f$ d’${\mathbb{R}}^4$ tal que

1. $\mathrm{Im}(f)\le \mathrm{Ker}(f)$; $f(1,1,0,0)=(0,1,0,0)$; $f(1,0,1,0)=(1,0,1,1)$;
2. $\mathrm{Ker}(f)\le \mathrm{Im}(f)$; $f(1,1,0,0)=(0,1,0,0)$; $f(1,0,1,0)=(1,0,1,1)$;

En cas d’existir, raona si aquest endomorfisme és únic.

Solució

Sense solució.

Qüestió 3.23

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials i siga $f:V_1⟶V_2$ una aplicació lineal. Siga $v_1\in V_1$ i $v_2\in V_2$ vectors tals que $f(v_1)=v_2$. Demostra

1. $⟨f^{-1}[\{v_2\}]⟩=⟨v_1⟩+\mathrm{Ker}(f)=f^{-1}[⟨v_2⟩]$;
2. $⟨v_2⟩=f[⟨v_1⟩]$.

Solució

Sense solució.

Qüestió 3.24

Siga $\mathbb{K}$ un cos i siguen natural $m,n\in \mathbb{N}$. Determina una base per al $\mathbb{K}$-espai vectorial ${\mathrm{Hom}}_{\mathbb{K}}({\mathbb{K}}^n,{\mathbb{K}}^m)$.

Solució

Sense solució.

Qüestió 3.25

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió finita $n\ge 1$. Demostra que $V$ és isomorf a ${\mathbb{K}}^n$. Enuncia (sense demostrar-los) els resultats que utilitzes.

Solució

Sense solució.

Qüestió 3.26

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $n$. Construeix explícitament un isomorfisme de $V$ en ${\mathbb{K}}^n$.

Solució

Sense solució.

Qüestió 3.27

Troba l’error en el següent raonament.

Sabem que $\mathbb{R}$ és un $\mathbb{R}$-espai vectorial. Considerem l’aplicació $f:\mathbb{R}⟶\mathbb{R}$ definida mitjançant $f(x)=x^2$. Es té que $$\mathrm{Ker}(f)=\{x\in \mathbb{R}\mid f(x)=0\}=\{x\in \mathbb{R}\mid x^2=0\}=\{0\}.$$ Així, $f$ és una aplicació injectiva.

Solució

Sense solució.

Qüestió 3.28

Siga $\mathbb{K}$ un cos i $\mathsf{A}\in {\mathrm{M}}_{m,n}(\mathbb{K})$. És cert que existeix una aplicació lineal $f:{\mathbb{K}}^n⟶{\mathbb{K}}^m$ que tinga a $\mathsf{A}$ com a matriu coordenada en les respectives bases canòniques? Justifica la resposta.

Solució

Sense solució.

Qüestió 3.29

Dóna un exemple d’aplicació lineal que no siga injectiva.

Solució

Sense solució.

Qüestió 3.30

Dóna un exemple d’aplicació lineal sobrejectiva.

Solució

Sense solució.

Qüestió 3.31

Troba l’expressió analítica d’una aplicació lineal $f:{\mathbb{R}}^3⟶{\mathbb{R}}^3$ que satisfaça

1. ${\dim }_{\mathbb{K}}(\mathrm{Ker}(f))=2$;
2. $f(1,0,0)=(1,1,1)$.

Solució

Sense solució.

Qüestió 3.32

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials i $f:V_1⟶V_2$ una aplicació lineal. Siguen $\{v_1,\cdots ,v_r\}$ i $\{v_1,\cdots ,v_r,v_{r+1},\cdots ,v_n\}$ bases per a $\mathrm{Ker}(f)$ i $V_1$, respectivament. Demostra que $\{f(v_{r+1}),\cdots ,f(v_n)\}$ és linealment independent.

Solució

Sense solució.

Qüestió 3.33

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $n$ i siga $f:V⟶V$ un endomorfisme. Siguen $\mathcal{B}$ i $\bar{\mathcal{B}}$ dues bases de $V$. És cert que si la matriu coordenada d’$f$ de $\mathcal{B}$ a $\bar{\mathcal{B}}$ és la matriu identitat ${\mathsf{I}}_n$, aleshores $f={\mathrm{id}}_V$?

Solució

Sense solució.

Qüestió 3.34

Siga $V$ un $\mathbb{K}$-espai vectorial i $f:V⟶V$ una aplicació lineal tal que $f(f(v))=f(v)$ per a tot $v\in V$. Demostra que $\mathrm{Ker}(f)\cap \mathrm{Im}(f)=\{0\}$.

Solució

Sense solució.

Qüestió 3.35

Siga $V$ un $\mathbb{K}$-espai vectorial i $f:V⟶V$ una aplicació lineal. És cert que $V=\mathrm{Ker}(f)+\mathrm{Im}(f)$?

Solució

Sense solució.

Qüestió 3.36

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $f:V⟶V$ una aplicació lineal tal que que, per a tota aplicació lineal $g:V⟶V$, es té que $\mathrm{Ker}(g)\subseteq \mathrm{Ker}(f)$. Determina l’aplicació lineal $f$.

Solució

Sense solució.

Qüestió 3.37

Es considera $\mathbb{C}$, el $\mathbb{C}$-espai vectorial estàndard de dimensió $1$. Considera l’aplicació que associa a cada nombre complexe el seu conjugat, és a dir, l’aplicació $$\begin{array}{rccl}f:& \mathbb{C}& ⟶& \mathbb{C}\\ & z& ⟼& \bar{z}\end{array}$$ És cert que $f$ és un automorfisme?

Solució

Sense solució.

Qüestió 3.38

Considera ${\mathbb{K}}^3$, el $\mathbb{K}$-espai vectorial estàndard de dimensió $3$. Demostra que existeix una aplicació lineal $f:{\mathbb{K}}^3⟶{\mathbb{K}}^3$ tal que la següent cadena d’inclusions és estricta $$\mathrm{Ker}({\mathrm{id}}_{{\mathbb{K}}^3})⊊\mathrm{Ker}(f)⊊\mathrm{Ker}(f^2)⊊\mathrm{Ker}(f^3).$$

Solució

Sense solució.

Qüestió 3.39

En l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^3$ es considera el subespai vectorial $$W=\{(x,y,z)\in {\mathbb{R}}^3|x-2y+z=0\}.$$

1. Troba una base ${\mathcal{B}}_W$ de $W$.
2. Troba una base ${\mathcal{B}}_3$ d’${\mathbb{R}}^3$ que continga a la base ${\mathcal{B}}_W$ de l’apartat i.
3. Dóna un isomorfisme $f:{\mathbb{R}}^2⟶W$. Demostra que és isomorfisme.
4. Troba la matriu coordenada d’$f$ de ${\mathcal{B}}_2$ a la base ${\mathcal{B}}_3$ de l’apartat 2., on ${\mathcal{B}}_2=\{(1,2),(1,-1)\}.$

Solució

Sense solució.

Qüestió 3.40

Siga $V$ un $\mathbb{K}$-espai vectorial i siga $f:V⟶V$ una aplicació lineal. Es defineixen les potències d’$f$ de manera recursiva com segueix $$\begin{array}{rl}{f}^0& ={\mathrm{id}}_V;\\ f^{n+1}& =f^n\circ f;\end{array}$$

Notem que, per a cada $n\in \mathbb{N}$, $f^n$ és una aplicació lineal.

1. Demostra que si $m$ i $n$ són naturals en $\mathbb{N}$ amb $m\le n$, aleshores $\mathrm{Ker}(f^m)\subseteq \mathrm{Ker}(f^n)$.
2. Demostra que, per a cada $n\in \mathbb{N}$, existeix una aplicació lineal $f:{\mathbb{K}}^n⟶{\mathbb{K}}^n$ tal que la següent cadena d’inclusions és estricta $$\mathrm{Ker}(f^0)⊊\mathrm{Ker}(f)⊊\mathrm{Ker}(f^2)⊊\cdots ⊊\mathrm{Ker}(f^n).$$

Solució

Sense solució.

Qüestió 3.41

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials. Demostra que el conjunt ${\mathrm{Hom}}_{\mathbb{K}}(V_1,V_2)$ d’aplicacions lineals entre $V_1$ i $V_2$ amb

1. Vector zero l’aplicació lineal nul·la, és a dir $$\begin{array}{rccl}0:& V_1& ⟶& V_2\\ & v& ⟼& 0\end{array}$$
2. Suma d’aplicacions lineals $f,g\in {\mathrm{Hom}}_{\mathbb{K}}(V_1,V_2)$ com segueix $$\begin{array}{rccl}f+g:& V_1& ⟶& V_2\\ & v& ⟼& f(v)+g(v)\end{array}$$
3. Producte d’una aplicació lineal $f\in {\mathrm{Hom}}_{\mathbb{K}}(V_1,V_2)$ i un escalar $\lambda \in \mathbb{K}$ com segueix $$\begin{array}{rccl}\lambda f:& V_1& ⟶& V_2\\ & v& ⟼& \lambda f(v)\end{array}$$ és un $\mathbb{K}$-espai vectorial.

Solució

Sense solució.

Qüestió 3.42

Es consideren els $\mathbb{R}$-espais vectorials ${\mathbb{R}}_{\le 2}[x]$, de polinomis sobre $\mathbb{R}$ amb grau fitat per $2$, i $\mathbb{R}$, l’$\mathbb{R}$-espai vectorial estàndard de dimensió $1$. Es considera l’aplicació $\phi$, que a cada polinomi en ${\mathbb{R}}_{\le 2}[x]$ li assigna la seua integral definida en l’interval $[0,1]$, és a dir $$\begin{array}{rccl}\phi :& {\mathbb{R}}_{\le 2}[x]& ⟶& \mathbb{R}\\ & p(x)& ⟼& {\int }_0^{1}p(x)dx\end{array}$$

1. Demostra que $\phi$ és una aplicació lineal.
2. Demostra que $\phi$ és sobrejectiva però no injectiva.
3. Dóna bases per a $\mathrm{Ker}(\phi )$ i per a $\mathrm{Im}(\phi )$.
4. Es consideren les bases ${\mathcal{B}}_{\mathsf{p}}=\{1,x,x^2\}$ i ${\mathcal{B}}_{\mathsf{c}}=\{1\}$, per a ${\mathbb{R}}_{\le 2}[x]$ i $\mathbb{R}$, respectivament. Dóna la matriu coordenada de $\phi$ de ${\mathcal{B}}_{\mathsf{p}}$ a ${\mathcal{B}}_{\mathsf{c}}$. Empra aquesta matriu per a determinar el valor de la integral $${\int }_0^1-\frac{x^2}{4}+1dx$$

Solució

Sense solució.

4. Rang i equivalència de matrius

Qüestió 4.1

Dóna la definició de matrius equivalents.

Solució

Sense solució.

Qüestió 4.2

Siga $\mathsf{A}\in {\mathrm{M}}_n(\mathbb{K})$. Demostra que $\mathsf{A}$ és invertible si i només si $\mathrm{rang}(\mathsf{A})=n$.

Solució

Sense solució.

Qüestió 4.3

Siga $n\in \mathbb{N}$, $\mathbb{K}$ un cos i $\mathsf{A},\mathsf{B}$ matrius invertibles en ${\mathrm{GL}}_n(\mathbb{K})$. Justifica que $\mathsf{AB}$ és invertible i troba la relació entre $(\mathsf{AB}{)}^{-1}$, ${\mathsf{A}}^{-1}$ i ${\mathsf{B}}^{-1}$.

Solució

Sense solució.

Qüestió 4.4

Siga $\mathsf{A}$ una matriu en ${\mathrm{M}}_n(\mathbb{K})$. Es considera el sistema d’equacions homogeni $\mathsf{AX}=\mathsf{0}$. Anomenem $V$ al $\mathbb{K}$-espai vectorial de solucions del sistema d’equacions anterior. Demostra que ${\dim }_{\mathbb{K}}(V)=n-\mathrm{rang}(\mathsf{A})$. (Ajuda: Considera l’endomorfisme de ${\mathbb{K}}^n$ que té a $\mathsf{A}$ com a matriu coordenada de la base canònica a la base canònica.)

Solució

Sense solució.

Qüestió 4.5

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $n$ i $f:V⟶V$ un endomorfisme. Siga $\mathcal{B}$ una base de $V$ i siga $\mathsf{A}\in {\mathrm{M}}_n(\mathbb{K})$ la matriu coordenada d’$f$ de $\mathcal{B}$ a $\mathcal{B}$. Demostra que $\mathsf{A}$ és invertible si i només si $f$ és un isomorfisme.

Solució

Sense solució.

Qüestió 4.6

Es consideren els $\mathbb{R}$-espais vectorials ${\mathbb{R}}^2$ i ${\mathbb{R}}^3$ i les bases ${\mathcal{B}}_2=\{(1,2),(1,0)\}$ i ${\mathcal{B}}_3=\{(0,-1,0),(1,1,0),(0,0,1)\}$ d’${\mathbb{R}}^2$ i ${\mathbb{R}}^3$, respectivament. Es considera l’aplicació lineal $f:{\mathbb{R}}^2⟶{\mathbb{R}}^3$ que té com a matriu coordenada de ${\mathcal{B}}_2$ a ${\mathcal{B}}_3$ a la matriu $$\mathsf{A}=\left[\begin{array}{cc}1& 2\\ 0& 1\\ -1& 0\end{array}\right]\in {\mathrm{M}}_{3,2}(\mathbb{R})$$ Determina dues bases ${\bar{\mathcal{B}}}_2$ i ${\bar{\mathcal{B}}}_3$ d’${\mathbb{R}}^2$ i ${\mathbb{R}}^3$, respectivament, per a les quals la matriu coordenada d’$f$ de ${\bar{\mathcal{B}}}_2$ a ${\bar{\mathcal{B}}}_3$ és una matriu per blocs del tipus $$\left[\begin{array}{cc}{\mathsf{I}}_r& \mathsf{0}\\ \mathsf{0}& \mathsf{0}\end{array}\right]$$

Solució

Sense solució.

Qüestió 4.7

Siguen $\mathsf{A}$ i $\bar{\mathsf{A}}$ dues matrius en ${\mathrm{M}}_{mn}(\mathbb{K})$ equivalents. Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials amb ${\dim }_{\mathbb{K}}(V_1)=n$ i ${\dim }_{\mathbb{K}}(V_2)=m$. Demostra que existeix una aplicació lineal $f:V_1⟶V_2$ i existeixen $$\begin{array}{}{\mathcal{B}}_1,{\bar{\mathcal{B}}}_1& \text{ bases de }{V}_1;\\ {\mathcal{B}}_2,{\bar{\mathcal{B}}}_2& \text{ bases de }{V}_2,\end{array}$$ per a les quals $$\begin{array}{}\mathsf{A}& \text{ és la matriu coordenada d’}f\text{ de }{\mathcal{B}}_1\text{ a }{\mathcal{B}}_2;\\ \bar{\mathsf{A}}& \text{ és la matriu coordenada d’}f\text{ de }\overline{{\mathcal{B}}_1}\text{ a }\overline{{\mathcal{B}}_2}.\end{array}$$ Enuncia els resultats que utilitzes.

Solució

Sense solució.

Qüestió 4.8

Siga $\mathsf{A}\in {\mathrm{GL}}_n(\mathbb{K})$ una matriu invertible. Demostra que $\mathsf{A}$ pot escriure’s com a producte de matrius elementals.

Solució

Sense solució.

Qüestió 4.9

Es considera una aplicació lineal $f:{\mathbb{R}}^3⟶{\mathbb{R}}^5$ tal que per a $\mathsf{A}$, la matriu coordenada d’$f$ respecte les bases ${\mathcal{B}}_3$ d’${\mathbb{R}}^3$ i ${\mathcal{B}}_5$ d’${\mathbb{R}}^5$ satisfà que $\mathrm{rang}(\mathsf{A})=1$. Calcula la dimensió de $\mathrm{Ker}(f)$.

Solució

Sense solució.

Qüestió 4.10

Demostra que existeixen tres endomorfismes d’${\mathbb{R}}^2$ tals que qualsevol matriu d’ ${\mathrm{M}}_2(\mathbb{R})$ és la matriu coordenada d’algun d’aquests endomorfismes en algunes bases adequades. Justifica la resposta.

Solució

Sense solució.

Qüestió 4.11

Siga $\mathsf{A}\in {\mathrm{GL}}_n(\mathbb{K})$ una matriu invertible. Siga $\mathcal{B}=\{e_1,\cdots ,e_n\}$ una base d’un $\mathbb{K}$-espai vectorial de dimensió $n$. Demostra que existeix una base $\bar{\mathcal{B}}$ per a la qual ${\mathsf{A}}^{\mathsf{t}}$ és una matriu canvi de base de $\mathcal{B}$ a $\bar{\mathcal{B}}$.

Solució

Sense solució.

Qüestió 4.12

Troba un subconjunt $S\subseteq {\mathrm{M}}_3(\mathbb{R})$ tal que

1. Si $\mathsf{A}$ i $\mathsf{B}$ pertanyen a $S$, aleshores $\mathsf{A}$ i $\mathsf{B}$ no són equivalents.
2. Si $T\subseteq {\mathrm{M}}_3(\mathbb{R})$ és un subconjunt que satisfà l’ítem i., aleshores $|T|\le |S|$.

Solució

Sense solució.

Qüestió 4.13

Siga $\mathsf{A}\in {\mathrm{GL}}_n(\mathbb{R})$ una matriu invertible. Demostra que podem passar d’$\mathsf{A}$ a ${\mathsf{A}}^{-1}$ mitjançant una seqüència finita d’operacions elementals per fila.

Solució

Sense solució.

Qüestió 4.14

Siguen $\mathsf{A},\mathsf{C}$ matrius en ${\mathrm{M}}_n(\mathbb{K})$. Demostra que $\mathrm{rang}(\mathsf{A}\mathsf{C})\le \mathrm{rang}(\mathsf{C})$.

Solució

Sense solució.

Qüestió 4.15

Siguen $\mathsf{A},\mathsf{C}$ matrius en ${\mathrm{M}}_n(\mathbb{K})$. Demostra que $\mathrm{rang}(\mathsf{A}+\mathsf{C})\le \mathrm{rang}(\mathsf{A})+\mathrm{rang}(\mathsf{C})$.

Solució

Sense solució.

Qüestió 4.16

Siguen $V_1$ i $V_2$ dos $\mathbb{K}$-espais vectorials finitament generats i siga $f:V_1⟶V_2$ una aplicació lineal. Siguen ${\mathcal{B}}_1$ i ${\mathcal{B}}_2$ bases de $V_1$ i $V_2$, respectivament. Es considera $\mathsf{A}$ la matriu coordenada d’$f$ de ${\mathcal{B}}_1$ a ${\mathcal{B}}_2$.

Demostra que existeix una base ${\bar{\mathcal{B}}}_2$ de $V_2$ de forma que la matriu coordenada d’$f$ de ${\mathcal{B}}_1$ a ${\bar{\mathcal{B}}}_2$ és la forma esglaonada reduïda per files d’$\mathsf{A}$.

Solució

Sense solució.

Qüestió 4.17

Siga $\mathsf{A}$ una matriu en ${\mathrm{M}}_{mn}(\mathbb{K})$. Demostra que són equivalents les següents proposicions. Enuncia els resultats que utilitzes.

1. $\mathsf{A}$ i ${\mathsf{A}}^{\mathsf{t}}$ són matrius equivalents;
2. $m=n$, és a dir, $\mathsf{A}$ és una matriu quadrada.

Es considera la matriu $$\mathsf{A}=\left[\begin{array}{cc}1& 3\\ 4& 10\end{array}\right]$$ Determina dues matrius invertibles $\mathsf{P},\mathsf{Q}\in {\mathrm{GL}}_2(\mathbb{R})$ tals que $\mathsf{PAQ}={\mathsf{A}}^{\mathsf{t}}$.

Solució

Sense solució.

5. Determinants

Qüestió 5.1

Determina els paràmetres $a,b\in \mathbb{R}$ per als quals la següent matriu és invertible $$\left[\begin{array}{cccc}1& a& a& a\\ 1& b& a& a\\ 1& a& b& a\\ 1& a& a& b\end{array}\right]$$

Solució

Sense solució.

Qüestió 5.2

Determina els paràmetres $a,b\in \mathbb{R}$ per als quals la següent matriu és invertible $$\left[\begin{array}{cccc}a+b& a& a& a\\ a& a+b& a& a\\ a& a& a+b& a\\ a& a& a& a+b\end{array}\right]$$

Solució

Sense solució.

Qüestió 5.3

Siga $\mathsf{C}\in {\mathrm{GL}}_n(\mathbb{K})$ una matriu invertible. Demostra que $\mathrm{Det}({\mathsf{C}}^{-1})={(\mathrm{Det}(\mathsf{C}))}^{-1}$.

Solució

Sense solució.

Qüestió 5.4

Siga $\mathsf{C}\in {\mathrm{M}}_3(\mathbb{R})$ una matriu tal que $\mathrm{Det}(\mathsf{C})=10$. Es considera la matriu $\mathsf{D}=5\mathsf{C}$. Obtín raonadament $\mathrm{Det}(\mathsf{D})$ i la relació que existeix entre ${\mathsf{C}}^{-1}$ i ${\mathsf{D}}^{-1}$.

Solució

Sense solució.

Qüestió 5.5

Calcula el determinant de la següent matriu $$\left[\begin{array}{cccc}1& 2& 3& 4\\ 2& 2& 3& 4\\ 3& 3& 3& 4\\ 4& 4& 4& 4\end{array}\right]$$

Solució

Sense solució.

Qüestió 5.6

Determina els paràmetres $a,b,c\in \mathbb{R}$ per als quals la següent matriu és invertible $$\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1+a& 1& 1\\ 1& 1& 1+b& 1\\ 1& 1& 1& 1+c\end{array}\right]$$

Solució

Sense solució.

Qüestió 5.7

Siguen $\mathsf{A},\mathsf{B}$ dues matrius equivalents en ${\mathrm{M}}_n(\mathbb{R})$. És cert que $\mathrm{Det}(\mathsf{A})=\mathrm{Det}(\mathsf{B})$?

Solució

Sense solució.

6. Semblança i valors propis

Qüestió 6.1

Siga $f$ un endomorfisme en ${\mathbb{R}}^3$ que té a $\mathsf{A}$ com a matriu coordenada en la base canònica. Suposem que $\mathrm{polcar}(\mathsf{A})=x(x-1)(x+1)$.

Demostra la veritat o falsedat de les següents afirmacions.

1. $\mathsf{A}$ és diagonalitzable.
2. Existeix $V\le {\mathbb{R}}^3$ amb $\dim (V)=1$ tal que $f(v)=v$, per a tot $v\in V$.

Solució

Sense solució.

Qüestió 6.2

Determina si la matriu $\mathsf{A}\in M_2(\mathbb{R})$ és diagonalitzable, on $$\mathsf{A}=\left[\begin{array}{cc}2& 1\\ -1& 0\end{array}\right].$$

Solució

Sense solució.

Qüestió 6.3

Siga $V$ un $\mathbb{K}$-espai vectorial de dimensió $n$ i siga $f\in {\mathrm{End}}_{\mathbb{K}}(V)$. Siga $\lambda$ un valor propi d’$f$. Demostra que $1\le d_{\lambda }\le {\alpha }_{\lambda },$ on $d_{\lambda }$ i ${\alpha }_{\lambda }$ denoten, respectivament, la multiplicitat geomètrica i la multiplicitat algebraica del valor propi $\lambda$.

Solució

Sense solució.

Qüestió 6.4

Siguen $\mathsf{A}$ i $\mathsf{B}$ dues matrius en $M_n(\mathbb{K})$. Demostra o dóna un contraexemple de l’enunciat

Si $\mathsf{A}$ és diagonalitzable, aleshores $\mathsf{B}$ és diagonalitzable

per als següents casos:

1. $\mathsf{A}$ i $\mathsf{B}$ són equivalents.
2. $\mathsf{A}$ i $\mathsf{B}$ són semblants.

Solució

Sense solució.

Qüestió 6.5

Siga $f$ un endomorfisme d’un $\mathbb{K}$-espai vectorial $V$. Demostra que les següents proposicions són equivalents

1. $\mathrm{polcar}f$ no té arrels en $\mathbb{K}$.
2. No existeix cap subespai vectorial $U\le V$ de dimensió $1$ amb $f[U]\le U$.

Solució

Sense solució.

Qüestió 6.6

Siga $f$ un endomorfisme diagonalitzable d’un $\mathbb{K}$-espai vectorial $V$. Demostra que si ${\lambda }_1,\dots ,{\lambda }_r$ són tots els valors propis d’$f$, aleshores $V=V_{{\lambda }_1}+\cdots +V_{{\lambda }_r}$.

Solució

Sense solució.

Qüestió 6.7

Dóna un exemple d’endomorfisme diagonalitzable $f$ en ${\mathbb{R}}^3$ tal que $0$ siga valor propi d’$f$, $(1,1,1)$ siga un vector propi associat a $1$ i la multiplicitat algebraica d’$1$ siga $2$.

Solució

Sense solució.

Qüestió 6.8

Siga $f$ un endomorfisme d’un $\mathbb{Q}$-espai vectorial $V$. És cert que $f$ és diagonalitzable si i només si per a tot valor propi d’$f$ la seua multiplicitat algebraica coincideix amb la seua multiplicitat geomètrica?

Solució

Sense solució.

Qüestió 6.9

Siga $f$ un endomorfisme d’un $\mathbb{C}$-espai vectorial $V$. És cert que $f$ és diagonalitzable si i només si per a tot valor propi d’$f$ la seua multiplicitat algebraica coincideix amb la seua multiplicitat geomètrica?

Solució

Sense solució.

Qüestió 6.10

Siga $f$ un endomorfisme d’un $\mathbb{K}$-espai vectorial $V$. Siguen ${\lambda }_1,\cdots ,{\lambda }_r$ tots els valors propis diferents d’$f$ amb multiplicitats geomètriques associades $d_1,\cdots ,d_r$, respectivament. És cert que $f$ és diagonalitzable si i només si $\sum _{i=1}^r{d}_i=\dim V$?

Solució

Sense solució.

Qüestió 6.11

Siguen $\mathsf{A}$ i $\mathsf{B}$ dues matrius en ${\mathrm{M}}_n(\mathbb{K})$. És cert que si $\mathsf{A}$ i $\mathsf{B}$ són semblants i $\mathsf{A}$ és diagonalitzable, aleshores $\mathsf{B}$ és diagonalitzable?

Solució

Sense solució.

Qüestió 6.12

Siguen $\mathsf{A}$ i $\mathsf{B}$ dues matrius en ${\mathrm{M}}_n(\mathbb{K})$. És cert que si $\mathsf{A}$ i $\mathsf{B}$ són diagonalitzables, aleshores $\mathsf{A}+\mathsf{B}$ també és diagonalitzable?

Solució

Sense solució.

Qüestió 6.13

Siguen $\mathsf{A}$ i $\mathsf{B}$ dues matrius semblants en ${\mathrm{M}}_n(\mathbb{K})$. Demostra que $\mathsf{A}$ té un vector propi associat a un valor propi $\lambda \in \mathbb{K}$ si i només si $\mathsf{B}$ té un vector propi associat al mateix valor propi $\lambda \in \mathbb{K}$.

Solució

Sense solució.

Qüestió 6.14

Siga $f:{\mathbb{R}}^2\to {\mathbb{R}}^2$ una aplicació lineal diagonalitzable. Siga $\mathcal{B}=\{e_1,e_2\}$ una base formada per vectors propis. Demostra que $e_1+e_2$ és vector propi si, i només si, $f=\lambda {\mathrm{id}}_{{\mathbb{R}}^2}$ per a algun $\lambda \in \mathbb{R}$.

Solució

Sense solució.

Qüestió 6.15

Dóna un exemple d’endomorfisme $f$ en ${\mathbb{R}}^3$ tal que $3$ siga valor propi d’$f$ amb multiplicitat algebraica $2$ i $(1,1,-1)$ siga un vector propi associat a $-1$. És $f$ diagonalitzable?

Solució

Sense solució.

Qüestió 6.16

Es considera l’endomorfisme $f$ d’${\mathbb{R}}^3$ que té a $\mathsf{A}$ com a matriu coordenada en la base $\bar{\mathcal{B}}=\{(1,0,-1),(1,-1,0),(0,0,1)\}$, on $$\mathsf{A}=\left[\begin{array}{ccc}1& -1& 0\\ 0& 1& 0\\ 1& 2& 2\end{array}\right]$$

1. Determina l’expressió analítica de l’endomorfisme $f$.
2. Determina si l’endomorfisme $f$ és diagonalitzable.
3. Dóna una relació de semblança entre la matriu $\mathsf{A}$ i la matriu coordenada d’$f$ en la base canònica.

Solució

Sense solució.

Qüestió 6.17

Siga $f$ un endomorfisme d’un $\mathbb{K}$-espai vectorial $V$. Demostra que si $v_1,v_2\in V-\{0\}$ són vectors propis associats a valors propis diferents, aleshores el conjunt $\{v_1,v_2\}$ és linealment independent.

Solució

Sense solució.

Qüestió 6.18

Demostra que tots els endomorfismes sobre l’espai vectorial $\mathbb{R}$ són diagonalitzables. Es cert el mateix enunciat per a l’espai vectorial ${\mathbb{R}}^n$, amb $n\ge 2$?

Solució

Sense solució.

Qüestió 6.19

Suposem que $\mathsf{A}$ és la matriu coordenada de l’endomorfisme $f:{\mathbb{R}}^2⟶{\mathbb{R}}^2$ en la base $\mathcal{B}=\{e_1,e_2\}$, on $$\mathsf{A}=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$$

1. Troba, si és possible, una base $\bar{\mathcal{B}}$ d’${\mathbb{R}}^2$ formada per vectors propis.
2. Calcula $\mathsf{B}$, la matriu coordenada d’$f$ en la base $\bar{\mathcal{B}}$.
3. Quina és la relació entre $\mathsf{B}$ i $\mathsf{A}$?

Solució

Sense solució.

Qüestió 6.20

Es considera l’ $\mathbb{R}$-espai vectorial ${\mathbb{R}}^3$. Determina un endomorfisme $f:{\mathbb{R}}^3⟶{\mathbb{R}}^3$ que satisfaça les següents característiques.

1. ${\dim }_{\mathbb{R}}(\mathrm{Im}(f))=2$
2. $(1,2,1)$ és vector propi associat al valor propi $1$.
3. $(0,1,-1)$ és vector propi associat al valor propi $0$.
4. $f$ no és diagonalitzable.

Una vegada determinat,

1. Dóna la matriu coordinada d’ $f$ en la base canònica d’ ${\mathbb{R}}^3$.
2. Les propietats descrites en l’enunciat garantitzen la unicitat de l’endomorfisme $f$?
3. Determina totes les possibilitats per al polinomi característic d’un endomorfisme que satisfaça les propietats descrites en l’enunciat.

Solució

Sense solució.

Qüestió 6.21

Es considera l’$\mathbb{R}$-espai vectorial ${\mathbb{R}}^3$ i l’endomorfisme $$\begin{array}{rccl}f:& {\mathbb{R}}^3& ⟶& {\mathbb{R}}^3\\ & (x,y,z)& ⟼& (x-3z,x+y-4z,-2z)\end{array}$$

Determina si $f$ és diagonalitzable.

Solució

Sense solució.

Qüestió 6.22

Siga $\mathbb{K}$ un cos amb característica diferent a $2$. Es considera un $\mathbb{K}$-espai vectorial $V$ amb ${\dim }_{\mathbb{K}}(V)=3$ i la base de $V$, $\mathcal{B}=\{e_1,e_2,e_3\}$. Siga $f:V⟶V$ una aplicació lineal i $\lambda \in \mathbb{K}$ un escalar.

1. Demostra que si $e_1$ i $e_1+e_2$ són vectors propis per a $\lambda$, aleshores $e_2$ també és propi per a $\lambda$.
2. És cert que si ${\dim }_{\mathbb{K}}(V_{\lambda })=2$, aleshores $f$ és diagonalitzable?
3. Siga $\mathsf{A}$ la matriu coordenada d’$f$ en la base $\mathcal{B}$. Suposem que $\mathsf{A}$ és diagonalitzable. És cert que $\mathsf{A}$ és semblant a una única matriu diagonal?

Solució

Sense solució.

7. Formes bilineals

Qüestió 7.1

Troba raonadament la signatura de la matriu $\mathsf{A}\in M_2(\mathbb{R})$, on $$\mathsf{A}=\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right].$$

Solució

Sense solució.

Qüestió 7.2

Siguen $\mathsf{A}$ i $\mathsf{B}$ dues matrius simètriques reals. És cert que si $det(\mathsf{A})>0$ i $det(\mathsf{B})>0$, aleshores $\mathsf{A}$ i $\mathsf{B}$ són congruents?

Solució

Sense solució.

Qüestió 7.3

Siga $f$ una forma bilineal d’un $\mathbb{K}$-espai vectorial $V$ i siga $\mathcal{B}$ una base de $V$. Demostra que $f$ és antisimètrica si i només si la matriu coordenada d’$f$ en $\mathcal{B}$ és antisimètrica.

Solució

Sense solució.

Qüestió 7.4

Siga $\mathsf{A}$ una matriu de tamany $n$ sobre $\mathbb{C}$ simètrica. Demostra que $\mathsf{A}$ és congruent a una matriu del tipus $\mathsf{diag}(1,\cdots ,1,0,\cdots ,0)$.

Solució

Sense solució.

Qüestió 7.5

Siga $\mathsf{A}=(a_{i,j}{)}_{i,j=1}^n$ una matriu simètrica de tamany $n$ sobre $\mathbb{R}$ amb signatura menor estricta que el seu rang. És cert que existeix un índex $i$ per al qual $a_{ii}<0$?

Solució

Sense solució.

Qüestió 7.6

Digues, de forma raonada, si les següents matrius sobre ${\mathrm{M}}_2(\mathbb{R})$ $$\mathsf{A}=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\mathsf{B}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

1. Són semblants.
2. Són congruents.

Solució

Sense solució.

Qüestió 7.7

És necessàriament cert que tota matriu real és congruent a una matriu diagonal?

Solució

Sense solució.

Qüestió 7.8

Siga $f$ una forma bilineal simètrica d’un $\mathbb{R}$-espai vectorial $V$ diferent a l’aplicació nula. Demostra que existeix un $v\in V$ tal que $f(v,v)\ne 0$.

Solució

Sense solució.

Qüestió 7.9

Siguen $\mathsf{A}$ i $\mathsf{B}$ matrius en ${\mathrm{M}}_n(\mathbb{Q})$. És cert que si $\mathsf{A}$ i $\mathsf{B}$ són congruents i $det(\mathsf{A})>0$, aleshores $det(\mathsf{B})>0$?

Solució

Sense solució.

Qüestió 7.10

Defineix rang d’una forma bilineal. Justifica que la definició té sentit.

Solució

Sense solució.

Qüestió 7.11

És cert que dues matrius simètriques en ${\mathrm{M}}_n(\mathbb{R})$ són con-gruents si, i només si, tenen el mateix rang?

Solució

Sense solució.

Qüestió 7.12

Dóna un exemple d’una forma bilineal simètrica $f$ definida en un $\mathbb{K}$-espai vectorial $V$ que satisfaça que $f(v,v)\ge 0$, $f(w,w)\ge 0$ i $f(v+w,v+w)\le 0$ per a dos vectors $v$ i $w\in V$. Demostra que el conjunt $W=\{v\in V\mid f(v,v)\ge 0\}$ no és, en general, subespai vectorial.

Solució

Sense solució.

Qüestió 7.13

És cert que dues matrius en ${\mathrm{M}}_n(\mathbb{C})$ són congruents si, i només si, tenen el mateix rang?

Solució

Sense solució.

Qüestió 7.14

Siguen $\mathsf{A}$ i $\mathsf{B}$ dues matrius congruents en ${\mathrm{M}}_n(\mathbb{R})$. És cert que si $\mathsf{A}$ és diagonalitzable, aleshores $\mathsf{B}$ també és diagonalitzable?

Solució

Sense solució.

Qüestió 7.15

Suposem que $\mathsf{A}$ és la matriu coordenada de la forma bilineal $g:{\mathbb{R}}^2\times {\mathbb{R}}^2⟶\mathbb{R}$ en la base $\mathcal{B}=\{e_1,e_2\}$, on $$\mathsf{A}=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$$

1. Troba, si és possible, una base $\bar{\mathcal{B}}$ d’${\mathbb{R}}^2$ ortogonal.
2. Calcula $\mathsf{C}$, la matriu coordenada de $g$ en la base $\bar{\mathcal{B}}$.
3. Quina és la relació entre $\mathsf{C}$ i $\mathsf{A}$?

Solució

Sense solució.

Qüestió 7.16

Dóna un exemple de forma bilineal simétrica $f$ sobre ${\mathbb{R}}^2$ de signatura $1$ i rang $2$ tal que $f((1,1),(1,-1))=2$.

Solució

Sense solució.

Qüestió 7.17

Siga $f$ una forma bilineal simètrica definida sobre un $\mathbb{K}$-espai vectorial $V$. Siguen $U$ i $W$ subespais vectorials de $V$. És cert que $(U+W{)}^{\perp }=U^{\perp }+W^{\perp }$?

Solució

Sense solució.

Qüestió 7.18

Quin és el subconjunt d’${\mathrm{M}}_n(\mathbb{R})$ format per les matrius congruents a alguna matriu diagonal?

Solució

Sense solució.

Qüestió 7.19

Siga $V$ un espai vectorial de dimensió major o igual a $2$. Troba l’expressió analítica d’alguna forma bilineal en $V$ per a la què existeix un vector $v\in V$ tal que $⟨v⟩=⟨v{⟩}^{\perp }$.

Solució

Sense solució.

Qüestió 7.20

Siga $\mathbb{K}$ un cos amb $\mathrm{car}(\mathbb{K})\ne 2$, siga $V$ un $\mathbb{K}$-espai vectorial i siga $f:V\times V⟶\mathbb{K}$ una forma bilineal sobre $V$. Demostra que les següents proposicions són equivalents.

1. $f$ és una forma bilineal simètrica.
2. Tota matriu coordenada d’$f$ és simètrica.
3. Existeix una base $\mathcal{B}$ de $V$ ortogonal per a $f$.
4. Existeix una matriu coordenada d’$f$ que és una matriu diagonal.
5. Tota matriu coordenada d’$f$ és congruent a una matriu diagonal.

Enuncia els resultats que utilitzes sense demostrar-los.

Solució

Sense solució.

8. Productes escalars

Qüestió 8.1

Siga $(V,\cdot )$ un espai vectorial euclidià. És necessàriament cert que $v\cdot w\ge 0$ per a tot $v,w\in V$?

Solució

Sense solució.

Qüestió 8.2

Siga $(V,\cdot )$ un espai vectorial euclidià. Siga $\{v_1,\cdots ,v_r\}$ un conjunt de vectors no nuls de $V$ ortogonals $2$ a $2$. Demostra que el conjunt $\{v_1,\cdots ,v_r\}$ és linealment independent.

Solució

Sense solució.

Qüestió 8.3

Troba una base ortogonal $\mathcal{B}$ de l’espai euclidià estàndard ${\mathbb{R}}^2$ tal que $(1,2)\in \mathcal{B}$.

Solució

Sense solució.

Qüestió 8.4

Siga $V$ un $\mathbb{R}$-espai vectorial i $f$ una forma bilineal simètrica sobre $V$. Demostra que $V$ té bases ortonormals si i només si $f$ és un producte escalar.

Solució

Sense solució.

Qüestió 8.5

Siga $\mathsf{A}=(a_{i,j}{)}_{i,j=1}^n$ una matriu simètrica de tamany $n$ sobre $\mathbb{R}$. És cert que si existeix un índex $i$ per al qual $a_{ii}\ge 0$ aleshores $\mathsf{A}$ és una matriu coordenada d’un producte escalar sobre ${\mathbb{R}}^n$?

Solució

Sense solució.

Qüestió 8.6

Siga $\mathsf{A}=(a_{i,j}{)}_{i,j=1}^n$ la matriu coordenada d’un producte escalar sobre ${\mathbb{R}}^n$ en una base $\bar{\mathcal{B}}$. És cert que existeix un índex $i$ per al qual $a_{ii}\ge 0$?

Solució

Sense solució.

Qüestió 8.7

Siga $V$ un espai vectorial euclidià de dimensió $2$. Siguen $\mathcal{B}=\{u,v\}$ i $\bar{\mathcal{B}}=\{u,w\}$ dues bases ortonormals de $V$. Demostra que $w=v$ o $w=-v$.

Solució

Sense solució.

Qüestió 8.8

Considerem l’espai vectorial euclidià estàndar $({\mathbb{R}}^4,\cdot )$. Calcula la projecció ortogonal del vector $(1,2,1,0)$ sobre l’espai vectorial $U=⟨(1,1,0,-1),(1,0,-2,2)⟩$.

Solució

Sense solució.

Qüestió 8.9

Dins l’espai euclidià estàndard $({\mathbb{R}}^3,\cdot )$, considerem el subespai vectorial $$U=⟨(1,2,0),(1,0,1)⟩.$$

1. Troba una base ortonormal d’$U^{\perp }$.
2. Calcula la projecció ortogonal del vector $(3,0,0)$ sobre $U^{\perp }$.

Solució

Sense solució.

Qüestió 8.10

Siga $f$ una forma bilineal simètrica regular d’un espai vectorial $V$. Siga $U\le V$. Demostra que $(U^{\perp }{)}^{\perp }=U$.

Solució

Sense solució.

Qüestió 8.11

Siga $(V,\cdot )$ un espai vectorial euclidià de dimensió $n$. Siguen $W$ i $U$ dos subespais de la mateixa dimensió $r\le n$. Demostra que existeix una isometria $f:V⟶V$ que satisfà $f[W]=U$.

Solució

Sense solució.

Qüestió 8.12

Siguen $f$ un producte escalar en un espai vectorial $V$ i $U$ un subespai de $V$ diferent a $\{0\}$. Considerem $f\upharpoonright {}_{U\times U}$, la restricció d’$f$ a $U$. Siga $\mathsf{A}$ la matriu coordenada d’$f\upharpoonright {}_{U\times U}$ en una base $\mathcal{B}$ d’$U$. Demostra que $det(\mathsf{A})>0$.

Solució

Sense solució.

Qüestió 8.13

Siga $(V,\cdot )$ un espai vectorial euclidià amb $\dim V=2$. Siga $u\in V$ tal que $u\cdot u=1$. Demostra que només hi ha dos formes possibles d’escollir un vector $v\in V$ de forma que el conjunt $\{u,v\}$ siga una base ortonormal.

Solució

Sense solució.

Qüestió 8.14

Es considera la forma bilineal $f$ d’${\mathbb{R}}^3\times {\mathbb{R}}^3$ en $\mathbb{R}$ que té a $\mathsf{A}$ com a matriu coordenada en la base $\bar{\mathcal{B}}=\{(0,0,-1),(1,-1,0),(1,0,1)\}$, on $$\mathsf{A}=\left[\begin{array}{ccc}1& -1& 0\\ -1& 2& 0\\ 0& 0& 1\end{array}\right]$$

1. És $f$ un producte escalar?
2. Determina l’expressió analítica d’$f$.
3. Utilitza Gram-Schmidt per obtindre a partir de $\bar{\mathcal{B}}$ una base ortonormal d’${\mathbb{R}}^3$.

Solució

Sense solució.

Qüestió 8.15

Siga $({\mathbb{R}}^3,\cdot )$ l’$\mathbb{R}$-espai vectorial euclidià estàndard de dimensió $3$. Considerem la base $\mathcal{B}=\{(1,0,1),(1,-1,1),(1,2,0)\}$ d’${\mathbb{R}}^3$. Obtín, si és possible, una nova base d’${\mathbb{R}}^3$ $$\bar{\mathcal{B}}=\{{\bar{e}}_1,{\bar{e}}_2,{\bar{e}}_3\}$$ que satisfaça les següents condicions:

1. $_{1} =(1,0,1) $;
2. ${1}, {2} =(1,0,1), (1,-1,1) $;
3. Els vectors de $\bar{\mathcal{B}}$ formen, dos a dos, un angle de $\frac{\pi }{4}$ radians.

Solució

Sense solució.

Qüestió 8.16

Es considera l’espai vectorial euclidià estàndard $({\mathbb{R}}^3,\cdot )$.

1. Troba, si és possible, una base ortonormal del subespai vectorial $U$ d’${\mathbb{R}}^3$ donat per $$U=\{(x,y,z)\in {\mathbb{R}}^3\mid x+2y+z=0\}$$
2. Determina, si és possible, una isometria $f\in {\mathrm{End}}_{\mathbb{R}}({\mathbb{R}}^3)$ que complisca que $f[V]=U$ on $V$ és el subespai vectorial d’${\mathbb{R}}^3$ donat per $$V=\{(x,y,z)\in {\mathbb{R}}^3\mid z=0\}.$$

Solució

Sense solució.

Qüestió 8.17

Siga $(V,\cdot )$ un espai vectorial euclidià, siga $U\le V$ i $v\in V$. És cert que si $v\notin U$, aleshores $v\in U^{\perp }$?

Solució

Sense solució.

Qüestió 8.18

Siga $f$ una forma bilineal simètrica en un $\mathbb{R}$-espai vectorial $V$. És cert que si $f$ no és un producte escalar, aleshores existeix $v\in V$ no nul tal que $f(v,v)=0$?

Solució

Sense solució.

Qüestió 8.19

Siga $(V,\cdot )$ un espai vectorial euclidià, $\mathcal{B}=\{e_1,\cdots e_n\}$ una base de $V$ i $h:V⟶V$ una aplicació lineal. Demostra que si l’equació $h(e_i)\cdot h(e_j)=e_i\cdot e_j$ se satisfà per a tot $1\le i,j\le n$, aleshores $h$ és injectiva.

Solució

Sense solució.

Qüestió 8.20

Siga $V$ un $\mathbb{R}$-espai vectorial amb ${\dim }_{\mathbb{R}}(V)=2$ i siga $\mathcal{B}=\{e_1,e_2\}$ una base de $V$. Es considera la forma bilineal $f:V\times V⟶\mathbb{R}$ que té a la següent matriu $$\mathsf{A}=\left[\begin{array}{cc}1& 2\\ 2& -1\end{array}\right]$$ com a matriu coordenada d’$f$ en la base $\mathcal{B}$.

1. Determina una base $\bar{\mathcal{B}}$ ortogonal per a $f$.
2. Determina $\bar{\mathsf{A}}$ la matriu coordenada d’$f$ en $\bar{\mathcal{B}}$.
3. Troba la relació de congruència entre $\mathsf{A}$ i $\bar{\mathsf{A}}$.
4. És $f$ un producte escalar?

Solució

Sense solució.

Qüestió 8.21

Siga $V$ un $\mathbb{R}$-espai vectorial amb ${\dim }_{\mathbb{R}}(V)=n$ i siga $\mathcal{B}=\{e_1,e_2,\cdots ,e_n\}$ una base de $V$. Siga $f:V\times V⟶\mathbb{K}$ una forma bilineal en $V$ que satisfà la següent condició

Per a tot $v\in V$, $f(v,v)\ge 0$.

És cert que $f$ és un producte escalar?

Solució

Sense solució.

Qüestió 8.22

Es considera l’ $\mathbb{R}$-espai vectorial euclidià estàndard $({\mathbb{R}}^2,\cdot )$. Determina l’expressió analítica de l’isometria $h:{\mathbb{R}}^2⟶{\mathbb{R}}^2$ donada per la reflexió sobre el subespai vectorial $W=⟨(1,1)⟩$.

$$

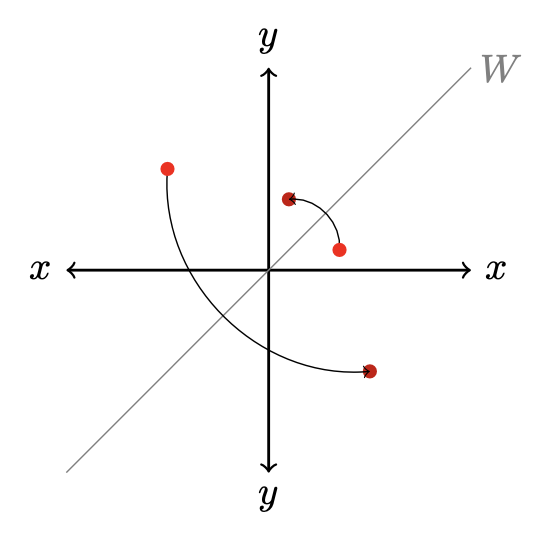
$\mathsf{Ajuda}$: Adoneu-vos que en esta situació podeu trobar dos vectors propis per a $h$. Fixeu una base adeqüada per al problema, considereu la matriu coordenada en aquesta base i després passeu-la a la base canònica.

Solució

Sense solució.

Qüestió 8.23

Siga $(V,\cdot )$ un $\mathbb{R}$-espai vectorial euclidià amb ${\dim }_{\mathbb{R}}(V)=n$. Siga $\mathcal{B}=\{e_1,\cdots ,e_n\}$ una base ortogonal de $V$. Demostra que $${\mathcal{B}}^{\prime }=\{\frac{e_1}{\parallel e_1\parallel },\cdots ,\frac{e_n}{\parallel e_n\parallel }\}$$ és una base ortonormal de $V$.

Solució

Sense solució.

Qüestió 8.24

Es considera l’$\mathbb{R}$-espai vectorial euclidià estàndard $({\mathbb{R}}^3,\cdot )$ i el subespai vectorial $U=⟨(1,0,1),(1,1,-2)⟩$.

1. Determina una base ortonormal per a $U$.
2. Calcula la projecció ortogonal del vector $(0,1,1)$ en $U$.

Solució

Sense solució.

9. Espai afí

Qüestió 9.1

Dóna la definició d’espai afí.

Solució

Sense solució.

Qüestió 9.2

Considerem l’espai afí estàndard ${\mathbb{R}}^3$. Determina les equacions cartesianes en el sistema de referència canònic de la menor varietat afí que conté els punts $$P=(1,0,1),Q=(2,0,2),R=(3,1,1).$$

Solució

Sense solució.

Qüestió 9.3

Sobre l’espai afí estàndard ${\mathbb{R}}^2$ es consideren els dos sistemes de referència afí següents. $${\mathcal{R}}_1=((0,1),\{(2,-2),(0,-1)\}),{\mathcal{R}}_2=((3,-1),\{(1,2),(-1,7)\})$$ Obtén les matrius afins de canvi de sistema de referència entre ${\mathcal{R}}_1$ i ${\mathcal{R}}_2$.

Solució

Sense solució.

Qüestió 9.4

Siguen $W_P$ i $U_Q$ dues varietats afins d’un espai afí $\mathcal{A}$. Demostra la següent igualtat entre varietats afins. $$W_P+U_Q=(W+U+⟨\overrightarrow{PQ}⟩{)}_P$$

Solució

Sense solució.

Qüestió 9.5

Considerem l’espai afí estàndard ${\mathbb{R}}^2$. Siga $P=(0,0)$. Calcula les coordenades de $P$ en el sistema de referència $$\mathcal{R}=((1,1);\{(1,1),(1,0)\})$$

Solució

Sense solució.

Qüestió 9.6

Sobre l’espai afí estàndard ${\mathbb{R}}^4$, determina el menor espai afí que conté els següents 4 punts $P=(1,3,0,0)$, $Q=(2,0,-1,1)$, $R=(3,0,1,1)$ i $S=(2,3,2,0)$. Determina les seues equacions cartesianes respecte el sistema de referència canònic. Quina és la dimensió d’aquest espai afí?

Solució

Sense solució.

Qüestió 9.7

Siguen $P$, $Q$ i $R$ tres punts en un espai afí $\mathcal{A}$. Demostra que l’espai afí $⟨\overrightarrow{QP},\overrightarrow{QR}{⟩}_P$ és el menor espai afí que conté els punts $P$, $Q$ i $R$.

Solució

Sense solució.

Qüestió 9.8

Sobre l’espai afí estàndard ${\mathbb{R}}^4$ es consideren els següents plànols. $$\begin{array}{rcl}{\mathrm{\Pi }}_1& =& \{(x,y,z,t)\in {\mathbb{R}}^4\mid y+3t-3=0,-2x-y+z+5=0\}\\ {\mathrm{\Pi }}_2& =& \{(x,y,z,t)\in {\mathbb{R}}^4\mid 2x-z-3t-2=0,2x+2y-z+3t-8=0\}\end{array}$$ Determina la seua posició relativa.

Solució

Sense solució.

Qüestió 9.9

Siga $(\mathcal{A},V,+)$ un espai afí. Siguen $P,Q\in \mathcal{A}$ i $v,w\in V$. Demostra que si $P+v=Q+w$, aleshores $\overrightarrow{PQ}=v-w$.

Solució

Sense solució.

Qüestió 9.10

Siga $\mathcal{A}$ un espai afí de dimensió $3$. Demostra que si dos plans distints ${\mathrm{\Pi }}_1$ i ${\mathrm{\Pi }}_2$ es tallen, aleshores ${\mathrm{\Pi }}_1\cap {\mathrm{\Pi }}_2$ és una recta.

Solució

Sense solució.

Qüestió 9.11

Siga $\mathcal{A}$ un espai afí de dimensió $3$ i siguen $P,Q,R\in \mathcal{A}$. Demostra que si existeix un únic pla que passa per $P,Q$ i $R$, aleshores $\dim ⟨\overrightarrow{PQ},\overrightarrow{PR}⟩=2$.

Solució

Sense solució.

Qüestió 9.12

Es considera l’ $\mathbb{R}$-espai afí estàndard $({\mathbb{R}}^3,{\mathbb{R}}^3,+)$. Es consideren els sistemes de referència afí següents $$\begin{array}{rl}{\mathcal{R}}_{\mathrm{c}}^{(3)},& \text{ el sistema de referència afí canònic d’ }{\mathbb{R}}^3\\ \bar{\mathcal{R}}& =((1,2,0);\{(1,2,1),(1,0,1),(1,0,0)\})\end{array}$$

1. Determina les equacions del canvi de sistema de referència de ${\mathcal{R}}_{\mathrm{c}}$ a $\bar{\mathcal{R}}$ i de $\bar{\mathcal{R}}$ a ${\mathcal{R}}_{\mathrm{c}}$.
2. Determina les equacions cartesianes en els dos sistemes de referència de la recta que passa pels punts $P=(0,0,1)$ i $Q=(1,0,0)$.

Solució

Sense solució.

10. Afinitats

Qüestió 10.1

Defineix afinitat entre espais afins. Pots donar un exemple d’una afinitat no bijectiva?

Solució

Sense solució.

Qüestió 10.2

Siga $\mathcal{A}$ un espai afí amb espai vectorial subjacent $V$. Siga $g$ un endomorfisme de $V$. Pots donar una afinitat $f:\mathcal{A}⟶\mathcal{A}$ tal que $\bar{f}=g$?

Solució

Sense solució.

Qüestió 10.3

Siga $f$ una afinitat d’un espai afí $\mathcal{A}$. Demostra que $f$ és injectiva si i només si $\bar{f}$ és injectiva.

Solució

Sense solució.

Qüestió 10.4

Siga $f$ una afinitat d’un espai afí $\mathcal{A}$. Demostra que $f$ és sobrejectiva si i només si $\bar{f}$ és sobrejectiva.

Solució

Sense solució.

Qüestió 10.5

Siga $\mathcal{A}$ un espai afí i siga $f:\mathcal{A}\to \mathcal{A}$ una aplicació afí. Siguen $W_P$ i $U_Q$ dues varietats afins dins d’$\mathcal{A}$. És cert que si $f[W_P]$ i $f[U_Q]$ es creuen, aleshores $W_P$ i $U_Q$ es creuen?

Solució

Sense solució.

Qüestió 10.6

Siga $(\mathcal{A},V,+)$ un espai afí euclidià i $f:\mathcal{A}⟶\mathcal{A}$ una afinitat. Siguen $P_1$, $P_2$ i $P_3$ tres punts colineals d’$\mathcal{A}$. Demostra que les respectives imatges per $f$, és a dir, $f(P_1)$, $f(P_2)$ i $f(P_3)$, tornen a ser tres punts colineals d’$\mathcal{A}$.

Solució

Sense solució.

Qüestió 10.7

Demostra que dos espais afins de la mateixa dimensió són isomorfs.

Solució

Sense solució.

Qüestió 10.8

Dóna un exemple d’afinitat en l’espai afí estàndard ${\mathbb{R}}^2$ que tinga a $\{(0,y)\in {\mathbb{R}}^2\mid y\in \mathbb{R}\}$ com a conjunt de punts fixos.

Solució

Sense solució.

Qüestió 10.9

Es considera la paràbola d’equació cartesiana $y=x^2$. Aquesta corba ve determinada pel conjunt de punts $\{(\lambda ,{\lambda }^2)\in {\mathbb{R}}^2\mid \lambda \in \mathbb{R}\}$, en blau a la gràfica. A aquest conjunt de punts li apliquem els següents moviments: En primer lloc li apliquem una simetria respecte l’eix $x$ i al conjunt de punts resultants els apliquem una translació de vector $(-4,12)$. Aquests moviments transformen la paràbola original en la paràbola roja de la gràfica.

1. Dóna la matriu afí d’aquest moviment.
2. Dóna l’equació cartesiana de la paràbola resultant.

$$

Solució

Sense solució.

Qüestió 10.10

Siga $\mathcal{A}$ un espai afí i siga $f:\mathcal{A}⟶\mathcal{A}$ una aplicació afí. És cert que si $\bar{f}$ és la identitat, aleshores $f$ és una translació?

Solució

Sense solució.

Qüestió 10.11

Siguen $(\mathcal{A},V,+)$ i $(\mathcal{B},U,+)$ dos espais afins. Siga $W\le V$ un subespai vectorial i $P$ un punt d’$\mathcal{A}$. Siga $f:\mathcal{A}⟶\mathcal{B}$ una afinitat amb aplicació subjacent $\bar{f}:V⟶U$. Demostra que, per a la varietat afí $W_P$, es té que $$f[W_P]=(\bar{f}[W]{)}_{f(P)}.$$

Solució

Sense solució.

Qüestió 10.12

Siga $(\mathcal{A},V,+)$ un espai afí i siga $f:\mathcal{A}⟶\mathcal{A}$ una afinitat amb aplicació lineal subjacent $\bar{f}:V⟶V$. Raona sobre la veritat o falsedat de les següents proposicions.

1. Si $P\in \mathcal{A}$ és un punt fixe per a $f$ i $v\in V$ un vector propi per a $\bar{f}$ associat a un valor propi no nul, aleshores existeix una recta $\mathsf{r}$ en $\mathcal{A}$ que satisfà que $f[\mathsf{r}]=\mathsf{r}$, és a dir, existeix una recta $f$-invariant.
2. Si existeix una recta $\mathsf{r}$ en $\mathcal{A}$ que satisfà que $f[\mathsf{r}]=\mathsf{r}$, és a dir si existeix una recta $f$-invariant, aleshores existeix $P\in \mathcal{A}$ un punt fixe per a $f$ i $v\in V$ un vector propi per a $\bar{f}$ associat a un valor propi no nul.

Solució

Sense solució.

11. Espai afí euclidià

Qüestió 11.1

Defineix isometria en un espai afí euclidià i enuncia una caracterització equivalent.

Solució

Sense solució.

Qüestió 11.2

Siga $\mathcal{A}$ un espai afí euclidià i siguen $W_P$ i $U_Q$ dues varietat afins d’$\mathcal{A}$. Demostra que existeixen $R\in W_P$ i $S\in U_Q$ tals que $\overrightarrow{RS}\in (W+U{)}^{\perp }$.

Solució

Sense solució.

Qüestió 11.3

Siga $\mathcal{A}$ un espai afí euclidà i $P,Q,R\in \mathcal{A}$. Demostra que les següents proposicions són equivalents.

1. $\mathrm{d}(P,Q{)}^2+\mathrm{d}(P,R{)}^2=\mathrm{d}(Q,R{)}^2$.
2. Els vectors $\overrightarrow{PQ}$ i $\overrightarrow{PR}$ són ortogonals.

Solució

Sense solució.

Qüestió 11.4

Siga $(\mathcal{A},V,+)$ un espai afí euclidà, $P,Q\in \mathcal{A}$ i $v\in V$. Demostra que $$\mathrm{d}(P,Q)=\mathrm{d}(P+v,Q,+v).$$ Dedueix que tota translació és sempre un moviment.

Solució

Sense solució.

Qüestió 11.5

Siga $\mathcal{A}$ un espai afí euclidià i siga $U_Q$ un subespai afí. Considerem l’aplicació $g:\mathcal{A}⟶\mathcal{A}$, que a cada punt $P\in \mathcal{A}$ li assigna ${\mathsf{P}}_{U_Q}(P)$, la seua projecció ortogonal respecte $U_Q$. És $g$ una afinitat?

Solució

Sense solució.

Qüestió 11.6

Siga $({\mathbb{R}}^n,{\mathbb{R}}^n,+)$ l’espai afí euclidià estàndard. Siga $f:{\mathbb{R}}^n⟶{\mathbb{R}}^n$ un moviment i siga $v\in {\mathbb{R}}^n$ un vector propi d’$\bar{f}$. Demostra que $f\circ t_v$ és igual a $t_v\circ f$ o igual a $t_{-v}\circ f$.

Solució

Sense solució.

Qüestió 11.7

Sobre l’espai afí estàndard ${\mathbb{R}}^2$ es considera l’homotècia de raó $2$ i centre $P=(1,3)$. Determina la seua matriu afí respecte el sistema de referència canònic. És aquesta aplicació afí un moviment sobre ${\mathbb{R}}^2$?

Solució

Sense solució.