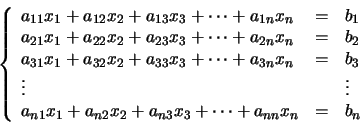6. Resolución de sistemas de ecuaciones lineales

El objetivo de este apartado es examinar los aspectos numéricos que se presentan al resolver sistemas de ecuaciones lineales de la forma:

$$\left\{ \begin{array}{lll} a_{11}x_{1} + a_{12}x_{2} + a_{1... ...x_{3} + \cdots + a_{nn}x_{n} & = & b_{n} \end{array} \right.$$ (42)

Se trata de un sistema de n ecuaciones con n incógnitas, x₁, x₂, ..., x_n. Los elementos a_ij y b_i son números reales fijados.

El sistema de ecuaciones (42) se puede escribir, empleando una muy útil representación matricial, como:

$$\begin{array}{llll} \left( \begin{array}{ccccc} a_{11} & a... ...} \\ b_{3} \\ \vdots \\ b_{n} \end{array} \right) \end{array}$$ (43)

Entonces podemos denotar estas matrices por A, x y b de forma que la ecuación se reduce simplemente a:

 

Ax=b (44)

Los métodos de resolución de sistemas de ecuaciones se pueden dividir en dos grandes grupos:

• Los Métodos exactos o algoritmos finitos que permiten obtener la solución del sistema de manera directa.
• Los Métodos aproximados que utilizan algoritmos iterativos e infinitos y que calculan las solución del sistema por aproximaciones sucesivas.

Al contrario de lo que pueda parecer, en muchas ocasiones los métodos aproximados permiten obtener un grado de exactitud superior al que se puede obtener empleando los denominados métodos exactos, debido fundamentalmente a los errores de truncamiento que se producen en el proceso.

De entre los métodos exactos analizaremos el método de Gauss y una modificación de éste denominado método de Gauss-Jordan. Entre los métodos aproximados nos centraremos en el estudio de los métodos de Richardson, Jacobi y Gauss-Seidel.