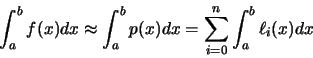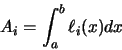Una estrategia muy útil para calcular el valor numérico de la integral
dada por la ecuación (74) consiste en reemplazar fpor otra función g, fácil de integrar, que aproxima a f de forma
adecuada. Si
![]() ,
se deduce que
,
se deduce que
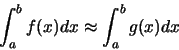
Supongamos que deseamos calcular la integral (74).
Podemos elegir una serie de nudos,
![]() en el
intervalo [a,b] e iniciar un proceso de interpolación de Lagrange
(ver apartado 7.1 para una descripción de los
polinomios de interpolación de Lagrange). El polinomio de grado menor
o igual a n que interpola a f en los nudos es:
en el
intervalo [a,b] e iniciar un proceso de interpolación de Lagrange
(ver apartado 7.1 para una descripción de los
polinomios de interpolación de Lagrange). El polinomio de grado menor
o igual a n que interpola a f en los nudos es:
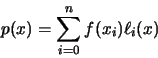 |
(75) |