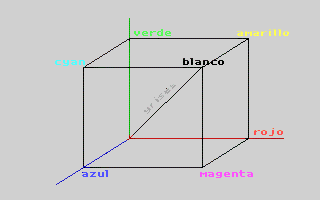
La reducción de los colores se basa fundamentalmente en una discretización del espacio de color RGB (en el que se encuentran definidos los colores de la imagen TRUE COLOR) dividiéndolo en cubos.
En un primer paso se calculan los rangos de variación de las distintas componentes RGB en la imagen. En realidad este paso es de poca utilidad puesto que las imágenes más agradables a la vista deben estar bastante contrastadas lo que implica que contenga colores, por una parte próximos al negro y por otra próximos al blanco con lo cual, en general, estaremos dividiendo todo el cubo RGB.

Posteriormente se discretizan todos los colores en la imagen asignándolos a uno de los cubos en los que se ha dividido la imagen, para posteriormente reducir el número de cubos al numero de colores deseados. Cada cubo representar un color que ser la media de todos los colores en el contenido.
Con esta información se construye una paleta y se representa la imagen en pantalla, ya sea asignando a los distintos colores su representante asociado al cubo al que pertenencen o utilizando técnicas de dithering.
Si el número de cubos conteniendo pixels de la imagen es superior al número de colores que deseamos en nuestra imagen final, es necesaria una reducción del número de cubos. Esta reducción se lleva a cabo asimilando los cubos que contienen el menor número de pixels al cubos que se encuentre m s próximo y por lo tanto que tendrá un representante lo más parecido posible al asociado al cubo que se desea eliminar.
La selección de los colores más representativos de una imagen es un asunto complicado. El algoritmo más simple para llevar a cabo esta tarea es el conocido como algoritmo de popularidad, en el que se considera que los colores más importantes son aquellos que aparecen con más frecuencia. Este algoritmo tiene como inconveniente que elimina colores que aún apareciendo en muy poca cantidad tienen una gran importancia en la calidad subjectiva final de la imagen. Supongamos que mediante un programa de renderizado 3D (por ejemplo mediante técnicas de raytracing) generamos una imagen de una esfera azul metálica iluminada por un punto de luz. Los tonos de azul serán los que más aparecerán, a excepción de unos pocos tonos claros en la región donde se refleja la luz (en nuestro programa 3D hemos caracterizado la esfera con reflexión especular). El algoritmo de popularidad eliminaría esos colores obteniéndose un resultado final de muy mala calidad. Si conservásemos estos tonos claros y eliminásemos algunos de los azules, el resultado sería mucho más agradable a la vista, ya que apenas notaríamos la diferencia entre dos tonos de azul muy parecidos.
De todo lo comentado en el parrafo anterior se deduce que más importante que la frecuencia de aparición de los puntos en la imagen, es la distancia entre los distintos puntos. Es mejor eliminar puntos muy parecidos aunque aparezcan muchas veces y sustituirlos por un sólo representante que eliminar colores que aún apareciendo pocas veces son muy distintos que el resto de los que aparecen en la imagen.
Un algoritmo más elaborado que el de la popularidad es el algoritmo del octree. Este algoritmo lleva a cabo una división recursiva del espacio RGB en cubos cada vez de menor tamaño. En una primera etapa se divide todo el cubo RGB, obteniéndose 8 nuevos cubos (de ahí su nombre octree -árbol de ocho en ocho-). Si alguno de los cubos no contiene pixels de imagen, el árbol ya no sigue creciendo en esa dirección. El algoritmo teórico, divide los cubos hasta que cada uno de ellos sólo contenga un pixels. En realidad no es necesario llegar a estos niveles, según lo expuesto anteriormente podríamos solamente dividir aquellos cubos en los que la varianza de los pixels en ellos contenidos fuese grande, de esta forma nos aseguramos de tener representados los colores más distintos de la imagen.
Este algoritmo en su forma original es muy poco práctico. Los árboles requieren una cantidad excesiva de memoria además de los requerimientos de almacenamiento de los pixels de la imagen (estamos hablando de tamaños de imagen de cerca del Megabyte de memoria). Se han desarrollado varias técnicas para solucionar estos problemas. En la práctica en lugar de un árbol se construye una matriz con tantas componentes como el número de colores al que deseemos reducir la imagen. Cada entrada en la matriz representar un cubo en el espacio RGB. Por otra parte se hace necesaria la utilización de una tabla hash para reducir el número de bits por pixel de 24bits a un valor apropiado, de forma que sea posible tener información de estos en memoria para el calculo de la varianza en cada uno de los cubos.
El algoritmo comienza con 8 cubos y asigna los pixels de la imagen a cada uno de ellos. Posteriormente calcula el de mayor varianza y genera 8 nuevas entradas en la matriz, ajustando las características de los cubos que sufren modificaciones. Este proceso se repite hasta conseguir un número de cubos iguales al numero de colores que deseamos reducir.
Este algoritmo obtiene unos resultados muy buenos, aunque de todas formas requiere bastante espacio de almacenamiento y las funciones hash a utilizar tienen una importante influencia sobre el resultado final de la imagen.
Como ya indicamos, la reducción se hace eliminando el cubo que contiene el menor número de pixels de imagen y de todo lo expuesto en esta sección se deduce que esta no es una opción excesivamente buena. Sería más recomendable la asimilación de los dos cubos más próximos en uno sólo, necesitando este proceso un número muy superior de operaciones al ser necesario el cálculo de distancias y una comparación exhaustiva entre todos los cubos disponibles. Cuando la reducción se lleva a cabo para un número elevado de colores, en general no vamos a tener problemas de eliminación de colores importantes, puesto que se realiza un ajuste muy fino y por lo tanto tendremos cubos con colores próximos a los que más aparecen y con pocas compoenentes que ser n eliminados, sin embargo cuando el número de colores al que queremos reducir se hace muy pequeño (32 ó 16 colores) esta división fina constituye un problema.
Si tenemos un ajuste muy fino del espacio RGB, y el número de colores al que queremos reducir la imagen es muy pequeño, tendremos que eliminar muchos cubos, en concreto los que tengan el menor número de pixels. Inicialmente eliminaremos colores próximos a los que más aparecen como se indicaba en el apartado anterior, pero al seguir reduciendo estaremos eliminando los colores importantes de los que hemos hablado y que tienen asociados muy pocos pixels de imagen. Para solucionar esto nuestro programa permite que el usuario indique manualmente el número de divisiones por componente RGB que se desea realizar. Cuando nos encontramos en este caso una división más gruesa nos lleva a tener que eliminar menos cubos (o incluso ninguno) siendo más probable que prevalezcan los cubos conteniendo esos colores importantes de aparición menor.
Otra cuestión importante es la de el remapeado de los pixels
de la imagen. En general, una vez que tenemos seleccionados los colores
más importantes de la imagen, asignamos a los pixels de la imagen
aquel color de entre los que disponemos que más se le parezca. Cuando
disponemos de un número elevado de colores, los resultados son bastante
buenos, pero cuando se hace una reducción a digamos 64, 32 o incluso
16 colores, se produce una pérdida de resolución, debida
a la asimilación en un sólo color de un número bastante
elevado de colores originales distintos (recuérdese que el número
de colores es igual al número de cubos y cuantos menos colores queramos
más grandes serán los cubos y más colores distintos
asimilarán en uno solo -la media de todos ellos-).