|
|
 |
|
Técnica de Umbral |
Técnica de Dithering |
En este punto se van a ver ciertos métodos de reducción de colores que dán un mejor resultado que los vistos con anterioridad. Pero para que la explicación sea más clara, vamos a realizar una reducción de grises, es decir, vamo a aplicar dithering a una imágen de 256 niveles de grises y la vamos a pasar a 16 grises. De esta forma, si queremos aplicar luego estos algoritmos a una imagen en color, simplemente habrá que aplicar la técnica a cada una de las componentes R, G y B de nuestra imagen.
Supongamos, como vimos anteriomente, que tenemos un ordenador que solo puede representar 16 colores (o niveles de grises) en pantalla, y nuestra imagen almacenada en memoria tiene 256(o niveles de grises) colores ¿cómo podemos tener una visualización lo más fidedigna posible de la imagen almacenada en memoria? Este problema se soluciona con las técnicas de dithering que procedemos a explicar a continuación.
Inicialmente estas técnicas eran utilizadas para convertir imágenes en tonos de grises a im genes monocromas, para poder visualizarlas en dispositivos de este tipo (pantallas de plasma, impresoras,...). La forma más sencilla de obtener una imagen monocromática es fijar un nivel de gris que constituye el umbral que nos indicar si el punto se pinta. Por ejemplo, si pintamos puntos blancos sobre fondo negro, una vez fijado el umbral, los puntos cuya intensidad lo sobrepase se pintarán de blanco, los demás no aparecerán, por lo tanto un umbral bajo producirá una imagen muy clara.
Sin embargo, distintas zonas de una imagen pueden ser tratadas con un valor de umbral proporcional al valor medio de sus intensidades, con lo cual mantenemos la información de contraste local, y obtenemos unos resultados mejores. Esto se observa claramente en el siguiente ejemplo.
|
|
 |
|
Técnica de Umbral |
Técnica de Dithering |
Este proceso genera una serie de falsos contornos que se pueden reducir mediante la adición de ruido pseudoaleatorio (los ordenadores no pueden generar números aleatorios, generan números pseudoaleatorios), es decir, se produce una reducción de las altas frecuencias en la imagen, los pasos del blanco al negro se hacen menos bruscos, puesto que el ojo tiende a promediar la intensidad localmente, simulando tonos de gris.
En la práctica se le añadía ruido a la imagen de grises y luego se procesaba con la técnica anteriormente descrita. Sumar ruido pseudoaleatorio a una imagen y luego someterla al proceso de paso a monocromo es equivalente a realizar un proceso con un umbral pseudoaleatorio sobre la imagen sin ruido, y en este punto es donde aparecen las matrices de dithering y el proceso conocido como "ordered dithering". Las matrices de dithering contienen estos valores umbrales pseudoaleatorios de los que hablábamos y la forma de generarlas es según una ecuación matricial recursiva, en la que se define la matriz de dithering por bloques.
Algunas matrices típicas son estas:
|
ó |
|
En el caso de las matrices 4x4 dividimos la imagen en grupos de 4x4 (obviamente) pixels a modo de tablero de ajedrez. De esta forma, superponiendo la matriz en cada recuadro, comparamos los valores de la imagen con el umbral que nos indica la matriz, si estamos por encima de éste, el punto aparece en pantalla.
Retomando nuestro objetivo inicial, en el que nos proponíamos reducir el número de grises de 256 a 16, indicamos la forma de utilizar el algoritmo del "ordered dithering" para nuestro propósito. Para representar 256 colores necesitamos 8 bits, y para 16 nos llegan 4 bits, lo cual nos simplifica ostensiblemente nuestra tarea.
El algoritmo trabaja de la siguiente forma: los 4 bits superiores del código de color a transformar, nos indican un nivel entre 16 dónde vamos a trabajar, por tanto se trata de aplicar el algoritmo monocromo a cada uno de estos 16 niveles, pintando el color de los 4 bits de mayor peso, si no es superado el umbral de la matriz de dithering o el nivel inmediato superior si es sobrepasado. Los cuatro bits de menor peso son los utilizados en la comparación con la matriz de dithering. Utilizando lenguaje C el algoritmo sería:
for (i=0;i<ancho_imagen;i++) {
x = i % 4;
for (j=0;j<alto_imagen;j++) {
in = imagen[i][j];
b0 =in >> 4;
if (b0+1>0xf) b1=0xf;
else b1 = b0+1;
vi = in & 0xf;
y = j % 4;
if (vi>matriz_dither[x][y]) pinta (i,j,b1);
else pinta (i,j,b0); } }
En el programa todas las variables son enteras, el operador % nos da el resto de la división entre los dos números indicados. El operador b0 =in >> 4 provoca un desplazamiento de 4 bits hacia la derecha de la variable in almacenando el resultado en b0 (lo cual es equivalente a una división por 16). El operador & en un AND lógico y el prefijo 0x indica que la constante está en hexadecimal.
Algoritmo de distribución del error
Este algoritmo en el caso de la reducción de 256 a 16 colores obtiene unos resultados muy semejantes al proceso anteriormente descrito, pero que ofrece una mayor versatilidad a la hora de trabajar con distintas cantidades de las indicadas.
Los algoritmos de distribución del error se basan en la sencilla idea de distribuir el error cometido en un pixel por los pixels adyacentes.
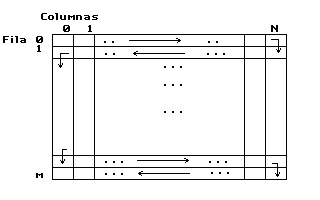
El algoritmo de distribución de error consiste en elegir de entre los niveles que podemos representar, aquel que minimice el error cometido, es decir, el que más se parezca al valor a representar menos el error asignado al pixel que estamos determinando. Una vez hecho esto calculamos el error, que no es más que la diferencia de ambos valores, y lo distribuímos entre los pixels adyacentes que todavía no hemos calculado. El más utilizado es el algoritmo de distribución del error de Floyd-Steinberg que distribuye el error entre los tres pixels adyacentes, según el esquema de la izquierda y siguiendo una dirección de rastreo como la indicada en el esquema de la derecha. Se trata del algoritmo de distribución del error de Floyd-Steinberg bidireccional.
|
|
 |
|
Distribución del error en Floyd-Steinberg |
Dirección de rastreo en Floyd-Steinberg |
Para almacenar el error cometido podemos utilizar una matriz de las mismas dimensiones de la matriz que contiene la imagen, en la que almacenamos los errores. En general en nuestro precario sistema gráfico, suele tener muy poca memoria y no vamos a tener sitio para una matriz de este tipo. Por eso es común utilizar algoritmos del tipo "scanline" ( de rastreo de línea) en el que utilizamos una matriz del ancho de la imagen y de alto 2 líneas (para el algoritmo de distribución del error de Floyd-Steinberg), de tal forma que una vez calculada la primera línea, en la segunda tenemos los errores acumulados de ésta. Así que para la siguiente línea copiamos la segunda en la primera e inicializamos la segunda.
La función en lenguaje de programación estructurado C que realiza el algoritmo de distribución del error de Floyd-Steinberg bidireccional es:
error =0;
for (j=0;j<ancho_imagen;j++) error_acumulado[[j][0] = error_acumulado[j][1] = 0;
for (j=0;j<ancho_imagen;j++) {
for (i=0;i<alto_imagen;i++) {
aux = imagen[i][j];
aux += error_acumulado[j][0]; /* Minimizamos la intensidad */
error = 100;
for (k=0;k<=niveles_representables;k++) {
imagen_color = color[k];
max = aux - imagen_color;
if (abs(max)<abs(error)) {
elegido = k;
error = max; } }
dither_image[i][j] = pinta[elegido]; /* Distribución del error con aritmética entera */
ee = error >> 2;
error_acumulado[i+1][1] += ee;
ee = (error - ee) >> 1;
error_acumulado[i+1][0] += ee;
ee = error - ee; error_acumulado[i][1] +=ee; }
for (k=0;k<ancho_imagen;k++) {
error_acumulado[k][0] = error_acumulado[k][1];
error_acumulado[k][1] =0; } }
En dónde todas las variables son enteras. La variable niveles_representables contiene el número de niveles que disponemos para visualizar en pantalla, y color[k] contiene el valor de nivel de gris, en el rango de la imagen a tratar, con el que minimizamos el error. La matriz pinta contiene la entrada de la paleta en la que se encuentra el tono de gris indicado por color[k].
Una última cosa antes de terminar, los colores que representamos en pantalla, se suelen tomar de la paleta de la imagen original, escogiendo según una cuantificación de color, de esta forma obtenemos los mejores resultados.