

|
La transformada Z es una herramienta matemática
que nos permite trabajar de una forma más cómoda con los sistemas discretos. La transformada Z básicamente asigna a una
secuencia discreta {f(k)} una función de variable compleja del siguiente modo:
|
|
|
|
La transformada Z tiene una serie de ventajas, que nos facilitan mucho el cálculo matemático, y simplifican mucho el trabajar con secuencias. Algunas de sus propiedades más importantes serian: |
PROPIEDADES DE LA TRANSFORMADA Z |
|
Linealidad
|
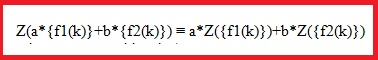 |
Desplazamiento
temporal
|
 |
Teorema del valor
inicial
|
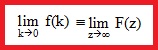 |
Teorema del valor
final
|
 |
| Las propiedades más reseñables quizas sean la del desplazamiento temporal, por su importancia con respecto a los retardos, y la del valor final, puesto que nos ayuda a conocer el limite de una secuencia. Existen más propiedades, como la de la convolución. Pero a niveles practicos esta nos ha parecido las más apropiadas. |
| Como es muy incomodo estar aplicando la formula que hemos puesto antes, hay tablas que nos ayudan con las transformaciones habituales. Como la transformada de Laplace y la Z van de la mano, en la siguiente tabla indicamos las transformaciones habituales relacionadas con Laplace: |
Dominio del tiempo (t)
Dominio de Laplace (s)
Dominio Z (z)
Impulso
1
1
Escalón
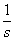
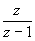
t
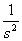
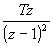
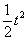
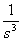
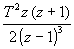
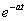
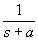
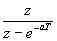
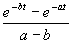

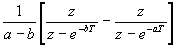
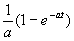
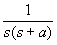
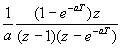
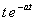
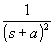
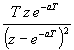
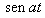
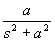
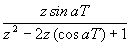
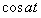
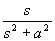
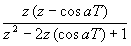
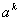
...
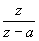
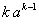
...
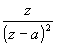
| La aplicación práctica de la transformada Z nos lleva a transformar funciones del plano continuo que están el Laplace al plano Z, y de este modo trabajar con ellas más fácilmente. Pero una vez se ha trabajado con ellas hay que devolverlas al plano de s, con lo que hay que antitransformar el plano Z. |
| Como la mayoría de procesos vienen dados como un cociente de polinomios en Z, pues se trata de simplificar al máximo para hacer que nuestras expresiones se parezcan a las expresiones que están indicadas en la tabla y así poder hacer el cambio contrario. Para simplificar al máximo se pueden usar dos métodos: la división polinómica o la descomposición en fracciones simples. La descomposición de fracciones simples suele dar mejores resultados, aunque perfectamente se puede usar en muchas ocasiones la división polinómica. |
| Pero para que estos dos últimos dos pasos queden más claros veamos dos ejemplos. Uno de división polinómica y otro de descomposición por fracciones simples. |
Ejemplo de división polinómica: |
| Teniendo la siguiente F(z)= |
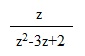 |
| Calcular la antitransformada por división polinómica. |
| Como vemos el método es coger el numerador e ir dividiéndolo por el denominador, como vemos en esta secuencia de imágenes: |
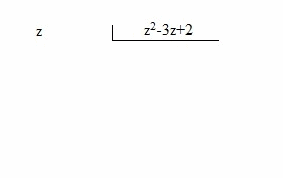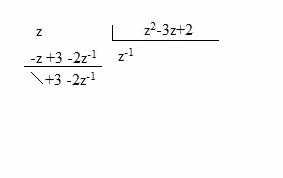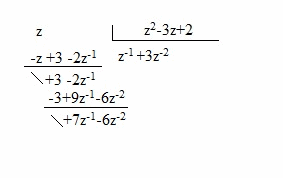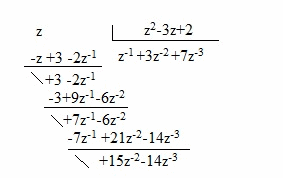 |
|
Una
vez tenemos el cociente de la división: z-1 + 3z-2 +7z-3
lo
antitransformamos y se nos queda convertido en una secuencia:
|
| {Fk}={0,1,3,7…} |
| Usando un poco la lógica, podemos intuir que la secuencia sigue el siguiente expresión: Fk = 2k -1 |
| Ver este paso puede ser costoso por lo que el metodo de “Descomposición de Fracciones Simples” se usa más a menudo puesto que nos ahorra este paso y es más mecanico |
Ejemplo de Descomposición de Fracciones Simples: |
| Teniendo la siguiente F(z)= |
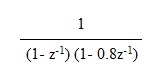 |
| Calcular la antitransformada por descomposición por fracciones simples. |
| En primer lugar descomponemos en fracciones simples: |
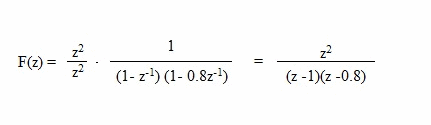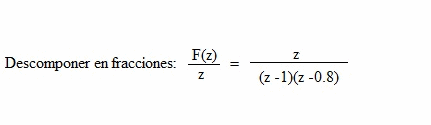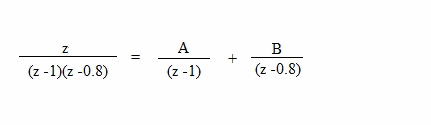 |
| A continuación se aplica el teorema de los residuos para extraer A y B: |
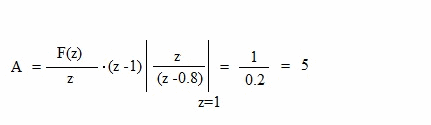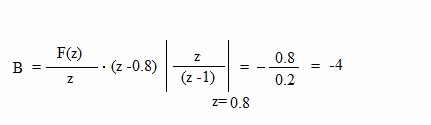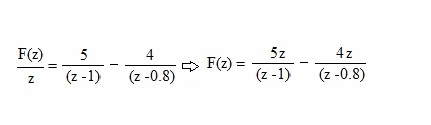 |
| De este modo llegamos a las expresiones últimas y por tablas de antitransformación obtenemos que: |
| {fk}= 5{1} – 4{0.8k} |
| Como vemos este metodo es más mecanico y menos costoso. Por ello es el más usado |
 |
 |