Como se ha intentado mostrar en la introducción, el estudio de la radiación del Cuerpo Negro fue fundamental para el desarrollo de la Teoría Cuántica.
En el experimento vamos a estudiar la radiación de un cuerpo incandescente. Para ello, utilizaremos una bombilla de manera que el cuerpo objeto de estudio será el filamento de tungsteno de ésta.
Vamos a hacer la hipótesis de que el filamento de tungsteno irradia como un cuerpo negro. Así, el espectro que seguirá su radiación debe de ajustarse a la distribución de Planck. Ésta será la hipótesis que pondremos a prueba en el laboratorio.
Una primera consecuencia derivada de la hipótesis es que la radiancia del filamento debe seguir la ley de Stefan-Boltzmann, cuestión que trataremos de comprobar.
Como la distribución de Planck, o la ley de Stefan-Boltzmann dependen de variables a las que no tenemos acceso directamente en el laboratorio (potencia, radiancia, frecuencia, temperatura), hemos de buscar la manera de encontrar expresiones que dependan de variables medibles en el laboratorio. Así:
1) Por conveniencia, no utilizaremos la expresión de esta distribución en función de la frecuencia, sino en función de la longitud de onda, que se escribe como:
(5)2) Para simplificar, consideraremos que estamos en la "región cuántica", es decir, a altas frecuencias, de manera que 
, y podemos aproximar la expresión (5) por:
(6)3) Consideraremos también que toda la potencia que suministra la bombilla será emitida por el filamento en forma de radiación, de manera que, de acuerdo con la ley de Stefan-Boltzmann, podemos escribir:
Hay que decir que haremos las simplificaciones de que la longitud, L, y la sección, S, del filamento permanecerán constantes en todo el régimen de funcionamiento y, además, que la sección del filamento es uniforme.
4) Por simplicidad técnica, en el experimento no vamos a reproducir el espectro del cuerpo negro, sino que estudiaremos la radiación a una longitud de onda fija (que conseguiremos situando un filtro ante la bombilla). Para medir la radiancia del filamento, utilizaremos un fotodiodo.
Un fotodiodo recibe radiación, y ofrece en su salida una diferencia de potencial, Vd, que es función de la radiación recibida; para bajas intensidades radiativas, vamos a suponer que la respuesta es lineal:
con C constante de proporcionalidad cuyo valor carece de interés para nuestros objetivos.
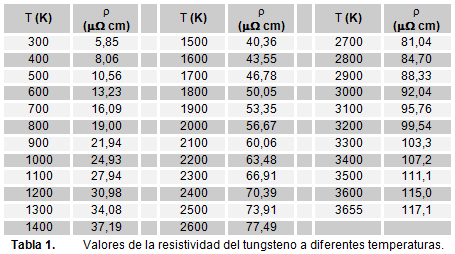
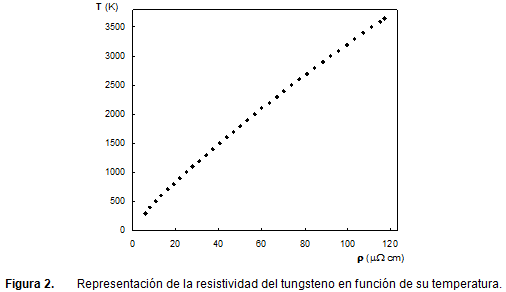
5) Por otro lado, necesitaremos conocer la temperatura a la que está el filamento de tungsteno, cuestión complicada, dada la inaccesibilidad de éste. Para ello, recurriremos a la variación de la resistividad, ρ, del tungsteno con la temperatura. Si analizamos la tabla de resistividades del tungsteno (Tabla 1), podemos ver que ésta se ajusta (Figura 2) a una expresión que supondremos del tipo:
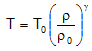(9)donde ρ0 es la resistividad de referencia a una temperatura T0 conocida. El exponente 
lo ajustaremos experimentalmente. Dadas las simplificaciones consideradas, la resistencia, R, que presenta el filamento y la resistividad vienen relacionadas según R = Lρ/S, de manera que podemos escribir:
(10)donde R0 es la resistencia de referencia a una temperatura T0 conocida (por ejemplo, a temperatura ambiente). La ventaja de la expresión (10) es que nos relaciona la temperatura (imposible de medir directamente) con la resistencia del filamento, que podemos obtener fácilmente.
Con las simplificaciones y consideraciones que hemos hecho hasta ahora, ya estamos en disposición de describir el montaje experimental y desarrollar expresiones que nos permitan comprobar nuestra hipótesis.
