3.1. Suma
La suma consistix a reunir dos quantitats. Amb ajuda de les plaques d’herbiniere-lebert, esta operació es representa unint dos plaques i veient la seua longitud total. 

Amb esta operació es pot treballar: 

Correspondència entre suma i longitud total.
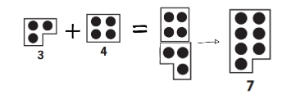
Exemple: 4 + 3
Agafes una placa del 4 i una altra del 3.
Les col·loques una al costat d'una altra.
Busques una placa que tinga la mateixa longitud total i descobriràs el resultat, en este cas seria una placa del 7.

Descomposició numèrica
Exemple: número 6
Agafes la placa del número elegit, en aquest cas el 6. 
Busques diferents combinacions amb altres plaques més xicotetes que quan les unisques tinguen la mateixa longitud que tens (6).
Trobes moltes combinacions possibles (1+5, 2+4, 3+3…).

Concepte de número com a resultat d’una combinació 
Exemple: Com es forma el 9?
S’indica a l’alumne que ajuntant diferents plaques han de formar el número 9
L’alumne busca combinacions possibles (6+3,2+7…).

Ús d’estrategies visuals com “fer 10” per facilitar la suma
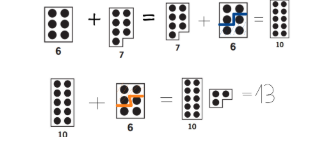
Exemple: 7 + 6
Agafes la placa del 7.
Per a arribar al 10, saps que necessites 3 més, per això li restes eixa part que et falta al número xicotet, al 6.
El 6 es descompon en 3+3. Per això, juntes la placa del 7 i la del 3 i obtens la placa del 10. I encara te queden 3 més per sumar-li així que ho juntes a la placa del 10 que havies format i obtens el resultat. 
 

Tot això beneficia als alumnes a reforçar la idea que els números es poden construir de diferents formes, a més permet treballar les sumes amb i sense portada, de manera concreta i finalment s'afavorix el raonament no verbal. 

3.2. Resta

La resta s'interpreta com “llevar” o “trobar la diferència”. Amb les plaques es pot treballar de dos maneres:

Llevar físicament una placa d’una altra més gran per veure quant queda.
Exemple: 9-3
Agafes la placa del 9.
Damunt o a un costat, col·loques la placa del 3, com si la restares.
La part que queda visible (sense la placa del 3 damunt) serà el resultat.

Buscar que número falta par completar una quantitat.
Exemple: 10 - 6
Col·loques la placa del 6 i et preguntes: Què necessite per poder arribar al 10?
Es comparen les longituds i veus que cada placa encaixa al lloc que queda, en aquest cat la placa del 4.

Tot això beneficia als alumnes a conéixer la relació entre la suma i la resta així com la complementarietat dels números (6+4=10, per això 10-4=6), també ajuda a desenrotllar estratègies de càlcul mental a través de la manipulació en este cas amb les plaques. 

3.3. Multiplicació

És difícil treballar amb només nombres menors que 10 a la multiplicació. Per això, és necessari canviar les plaques, sempre que no siguen nombres molt grans; així, es pot treballar simultàniament la composició i descomposició dels nombres d’una manera visual.

Per multiplicar amb aquest mètode, repetirem les plaques del nombre que hem de multiplicar ordenadament fins a aconseguir la solució d’una manera visual. Per això, s’ha de posar les plaques juntes.

Per exemple: 4 x 3 = 12

Doncs, en aquest cas repetirem 4 vegades la placa del 3, o 3 vegades la placa del 4, per exemple, aquesta última:

     

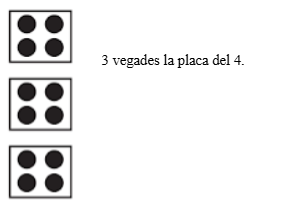
El resultat es passa de 10, per esbrinar-lo podem descompondre el nombre en una placa de 10 i una de 2, o una de 8 i altra de 4… El resultat és equivalent a aquestes plaques juntes. També es poden comptar els punts, però s'hauria d'aconseguir la descomposició.

Amb aquest mètode, es pot visualitzar la multiplicació com a suma repetida. A més, s'identifiquen certs patrons que tenen a veure amb la paritat o imparitat dels nombres.

3.4. Divisió

Treballar la divisió amb aquest mètode és paregut al de la multiplicació, però de forma contrària, doncs, en compte de juntar les plaques, el que es fa és repartir o agrupar, un nombre de plaques en parts iguals.

Per exemple, en la següent divisió:

12: 3

Hem de crear una placa de 12, per això podem utilitzar una placa de 10 i una de 2, una de 8 més altra de 4, o 2 de 6, com hem vist a l’apartat anterior.

Després, hem de repartir eixos 12 en 3 parts iguals, és a dir, en 3 grups. Per exemple, podem agafar tres plaques del nombre 4, d’aquesta manera fem 3 grups de 4. Es tracta d’anar provant amb les plaques, fins que les plaques juntes siguen iguals o equivalents al 12, en aquest cas amb 3 plaques, perquè hem de fer 3 grups iguals, al dividir-se entre 3.

Per exemple:

   

                                                                             

Aleshores, el resultat, són 3 plaques de 4, per tant, 4 és la solució de la divisió.

12: 3 = 4

Per tant, en aquest mètode, a la divisió es treballa de forma visual el fet de repartir o agrupar, per tant, es pot veure respecte a l’apartat anterior la relació entre la divisió i multiplicació. A més, es pot vore també de forma visual si la divisió és exacta o no, depenent del resto.