La curtòsi és el grau d'apuntament de la distribució. Per fer una idea intuïtiva considerem els següents grups de dades:

A: 3,4,4,4,5,5,5,5,5,6,6,6,7

B: 4,4,5,5,5,5,5,5,5,6,6

C: 3,3,4,4,4,5,5,5,5,6,6,6,7,7

Al grup B la major part de les puntuacions és troben al voltant del 5 (que marca el punt central per les tres distribucions). Al grup C les dades estan més allunyades del 5, i al grup A les dades no són ni tan a prop com al grup B ni tan separades com al grup C: les distribucions son diferents, i ho veurem millor si fem un cop d'ull a les corbes suavitzades de les tres distribucions:

La distribució B és més "apuntada" que la distribució C, que és més "plana".

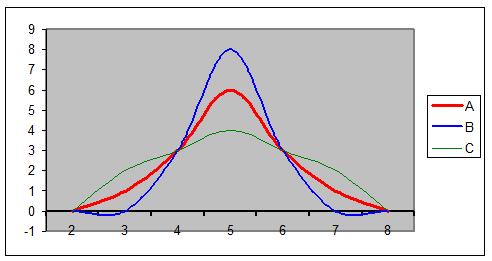
L'índex de curtòsi de Pearson és:

 

Com a exemple es mostra el càlcul de l'índex del grup C:

En primer lloc cal obtindre la mitjana i la desviació típica:

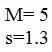
Seguidament obtenim les diferències de cada puntuació respecte de M, elevant a la quarta cadascuna de les diferències

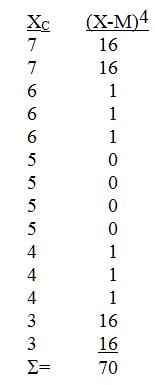
Substituint a la fórmula:

 

El signe negatiu indica que la distribució C és més aplanada que la distribució normal.

Els valors que pren l'índex de Pearson són :

a) 0 si l'apuntament de la distribució és el mateix de la distribució anomenada "normal".

b) Negatiu si la distribució és menys apuntada que la distribució normal, i direm que la distribució és platicúrtica.

c) Positiu si la distribució és més apuntada que la distribució normal, i direm que la distribució és leptocúrtica.