a) Supuestos:

La población sigue la distribución Normal.

Los datos son independientes.

b) Hipótesis:

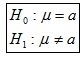
donde la "a" representa el valor que asignamos al parámetro.

c) Estadístico de contraste:

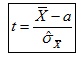
donde

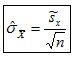
d) Distribución del estadístico de contraste: t con n-1 grados de libertad.

e) Significación del estadístico de contraste.

g) Intervalo de confianza:

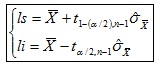
l_s y l_i son los límites superior e inferior del intervalo.

 

Ejemplo

Según la teoría del síndrome posvacacional el efecto de las vacaciones es positivo para la fatiga laboral. Otra teoría establece lo contrario porque la alteración de la rutina haría más grande la sensación subjetiva de fatiga. Para poner a prueba esta hipótesis seleccionan una muestra aleatoria de trabajadores de empresas de servicios a la vuelta de vacaciones y les administran una prueba de fatiga, resultando una Media igual a 25. Como la Media de la población es igual a 34, se pide decidir cuál de las dos explicaciones parece más razonable.

(n= 100, sigma= 9, alfa=0.05)

a) Supuestos: Dado que las muestras han sido generadas aleatoriamente, es razonable suponer que los datos son independiente.

b) Hipótesis:

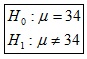
(Asignamos a la Media el valor 34 porque inicialmente se asume que la muestra pertenece a la población general, esto es, que las vacaciones no hacen ningún efecto en la sensación de fatiga)

c) Estadístico de contraste:

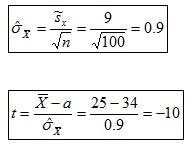
d) Distribución del estadístico de contraste: t con 99 grados de libertad.

e) Significación del estadístico de contraste: 0.0

f) Decisión: Dado que la significación del estadístico de contraste es inferior a 0.05, se rechaza la Hipótesis Nula.

g) Intervalo de confianza:

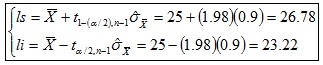
El parámetro de la población a que pertenece la muestra tiene un valor entre 23.22 y 26.78 (con un nivel de confianza de del 95%).

Conclusión: La evidencia obtenida no da apoyo a la Hipótesis de que la muestra pertenece a la población cuya Media es igual a 34. En consecuencia pensamos que muy probablemente las vacaciones tienen efecto positivo en la sensación de fatiga.