a) Supuestos:

La población sigue la distribución Normal.

Los datos son independientes.

b) Hipótesis:

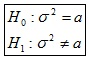
c) Estadístico de contraste:

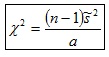
d) Distribución del estadístico de contraste: Ji Cuadrado con n-1 grados de libertad.

e) Significación del estadístico de contraste.

f) Intervalo de confianza:

 

 

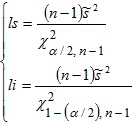
Ejemplo

Unos psicólogos piensan que una terapia nueva no mejora el sido de los pacientes de depresión, pero sí reduce la variabilidad. Para probarlo seleccionan una muestra aleatoria de pacientes a los que aplican la nueva terapia. Poner a prueba la Hipótesis de que los pacientes de depresión a los que han administrada la terapia presentan la misma variabilidad que los pacientes a los que no la han administrada. (a=.05)

Datos:

Varianza de la población: 8

Cuasivarianza obtenida en la muestra de pacientes a los que administran la terapia: 7

Tamaño de la muestra: 20

a) Supuestos: Dado que la muestra ha sido generada aleatoriamente se supone que los datos son independientes.

b) Hipótesis:

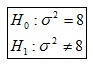
c) Estadístico de contraste:

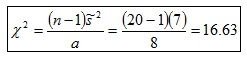
d) Distribución del estadístico de contraste: Ji Cuadrado con 19 grados de libertad.

e) Significación del estadístico de contraste: 0.61

f) Decisión: La significación del estadístico de contraste es mayor que el valor de alfa (0.05). En consecuencia, se acepta la Hipótesis Nula.

g) Intervalo de confianza:

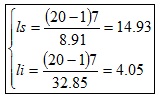
Con un nivel de confianza del 95% pensamos que la varianza poblacional se sitúa entre 4.05 y 14.93

 

Conclusión: Los datos recogidos respaldan la hipótesis de que la nueva terapia reduce las diferencias en el estado de los pacientes.