


Next: 4.2
Método de las Up: 4.
Cálculo de raíces Previous: 4.
Cálculo de raíces
4.1 Método de la bisección
Es el método más elemental y antiguo para determinar las
raíces de una ecuación. Está basado directamente en
el teorema de Bolzano explicado con anterioridad. Consiste en partir de
un intervalo [x0,x1]tal
que f(x0)f(x1)
< 0, por lo que sabemos que existe, al menos, una raíz real.
A partir de este punto se va reduciendo el intervalo sucesivamente hasta
hacerlo tan pequeño como exija la precisión que hayamos decidido
emplear.
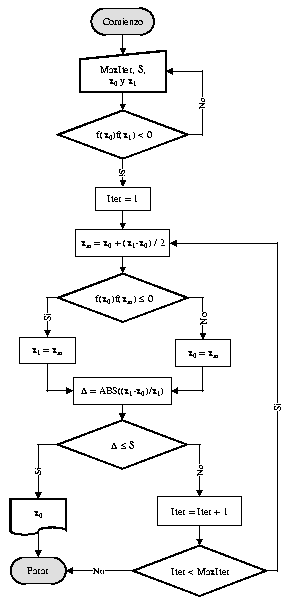
Figure: Diagrama de flujo correspondiente
a la implementación del método de la bisección.
|
[scale=0.9]eps/bisecc
|
El algoritmo empleado se esquematiza en la figura (3).
Inicialmente, es necesario suministrar al programa el número máximo
de iteraciones MaxIter, la tolerancia 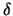 ,
que representa las cifras significativas con las que queremos obtener la
solución y dos valores de la variable independiente, x0
y x1, tales que cumplan la relación f(x0)f(x1)
< 0. Una vez que se comprueba que el intervalo de partida es adecuado,
lo dividimos en dos subintervalos tales que
,
que representa las cifras significativas con las que queremos obtener la
solución y dos valores de la variable independiente, x0
y x1, tales que cumplan la relación f(x0)f(x1)
< 0. Una vez que se comprueba que el intervalo de partida es adecuado,
lo dividimos en dos subintervalos tales que ![$[x_{0}, \frac{x_{0} + x_{1}}{2}]$](img130.gif) y
y ![$[\frac{x_{0} + x_{1}}{2}, x_{1}]$](img131.gif) y determinamos en qué subintervalo se encuentra la raíz (comprobando
de nuevo el producto de las funciones). Repetimos el proceso hasta alcanzar
la convergencia (hasta que
y determinamos en qué subintervalo se encuentra la raíz (comprobando
de nuevo el producto de las funciones). Repetimos el proceso hasta alcanzar
la convergencia (hasta que 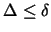 )
o bien hasta que se excede el número de iteraciones permitidas (Iter
> MaxIter), en cuyo caso es necesario imprimir un mensaje de error
indicando que el método no converge.
)
o bien hasta que se excede el número de iteraciones permitidas (Iter
> MaxIter), en cuyo caso es necesario imprimir un mensaje de error
indicando que el método no converge.
Dos operaciones representadas en el esquema de la figura (3)
requieren una explicación adicional:
-
El punto medio del intervalo se calcula como
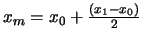 en lugar de emplear
en lugar de emplear 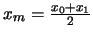 .
Se sigue de este modo una estrategia general al efectuar cálculos
numéricos que indica que es mejor calcular una cantidad añadiendo
un pequeño término de corrección a una aproximación
obtenida previamente. Por ejemplo, en un computador de precisión
limitada, existen valores de x0 y x1
para los cuales xm calculado mediante
.
Se sigue de este modo una estrategia general al efectuar cálculos
numéricos que indica que es mejor calcular una cantidad añadiendo
un pequeño término de corrección a una aproximación
obtenida previamente. Por ejemplo, en un computador de precisión
limitada, existen valores de x0 y x1
para los cuales xm calculado mediante 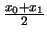 se sale del intervalo [x0,x1].
se sale del intervalo [x0,x1].
-
La convergencia (
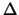 )
se calcula mediante la expresión
)
se calcula mediante la expresión  .
De este modo, el término
.
De este modo, el término 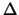 ,
representa el número de cifras significativas con las que obtenemos
el resultado.
,
representa el número de cifras significativas con las que obtenemos
el resultado.



Next: 4.2
Método de las Up: 4.
Cálculo de raíces Previous: 4.
Cálculo de raíces
Wladimiro Diaz Villanueva
1998-05-11


![]() ,
que representa las cifras significativas con las que queremos obtener la
solución y dos valores de la variable independiente, x0
y x1, tales que cumplan la relación f(x0)f(x1)
< 0. Una vez que se comprueba que el intervalo de partida es adecuado,
lo dividimos en dos subintervalos tales que
,
que representa las cifras significativas con las que queremos obtener la
solución y dos valores de la variable independiente, x0
y x1, tales que cumplan la relación f(x0)f(x1)
< 0. Una vez que se comprueba que el intervalo de partida es adecuado,
lo dividimos en dos subintervalos tales que ![]() y
y ![]() y determinamos en qué subintervalo se encuentra la raíz (comprobando
de nuevo el producto de las funciones). Repetimos el proceso hasta alcanzar
la convergencia (hasta que
y determinamos en qué subintervalo se encuentra la raíz (comprobando
de nuevo el producto de las funciones). Repetimos el proceso hasta alcanzar
la convergencia (hasta que ![]() )
o bien hasta que se excede el número de iteraciones permitidas (Iter
> MaxIter), en cuyo caso es necesario imprimir un mensaje de error
indicando que el método no converge.
)
o bien hasta que se excede el número de iteraciones permitidas (Iter
> MaxIter), en cuyo caso es necesario imprimir un mensaje de error
indicando que el método no converge.