4.3 Método de Newton  4. Cálculo de raíces  4.1 Método de la

   
4.2 Método de las aproximaciones sucesivas

Dada la ecuación f(x) = 0, el método de las aproximaciones sucesivas reemplaza esta ecuación por una equivalente, x=g(x), definida en la forma g(x)=f(x)+x. Para encontrar la solución, partimos de un valor inicial x₀ y calculamos una nueva aproximación x₁=g(x₀). Reemplazamos el nuevo valor obtenido y repetimos el proceso. Esto da lugar a una sucesión de valores 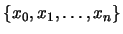$\{x_{0},x_{1},\dots,x_{n}\}$, que si converge, tendrá como límite la solución del problema.
 
    

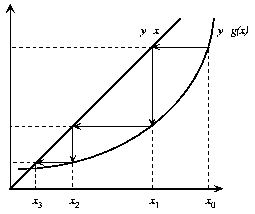
Figure: Interpretación geométrica del método de las aproximaciones sucesivas.

[scale=0.9]eps/as-1

  

En la figura (4) se representa la interpretación geométrica del método. Partimos de un punto inicial x₀ y calculamos y = g(x₀). La intersección de esta solución con la recta y=x nos dará un nuevo valor x₁ más próximo a la solución final.

Sin embargo, el método puede divergir fácilmente. Es fácil comprobar que el método sólo podrá converger si la derivada g'(x) es menor en valor absoluto que la unidad (que es la pendiente de la recta definida por y=x). Un ejemplo de este caso se muestra en la figura (5). Esta condición, que a priori puede considerarse una severa restricción del método, puede obviarse fácilmente. Para ello basta elegir la función g(x) del siguiente modo:

$$g(x) = x + \alpha f(x)$$

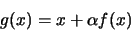
de forma que tomando un valor de 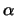$\alpha$ adecuado, siempre podemos hacer que g(x) cumpla la condición de la derivada.
 
 

   

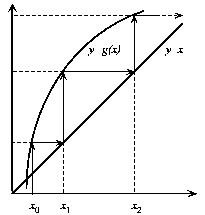
Figure: Demostración gráfica de que el método de las aproximaciones sucesivas diverge si la derivada g'(x) > 1.

[scale=0.9]eps/as-2

  

1998-05-11