4.4 Método de la  4. Cálculo de raíces  4.2 Método de las

   
4.3 Método de Newton

Este método parte de una aproximación inicial x₀ y obtiene una aproximación mejor, x₁, dada por la fórmula:

$$x_{1} = x_{0} - \frac{f(x_{0})}{f'(x_{0})}$$ (29)

 

La expresión anterior puede derivarse a partir de un desarrollo en serie de Taylor. Efectivamente, sea r un cero de f y sea x una aproximación a r tal que r=x+h. Si f'' existe y es continua, por el teorema de Taylor tenemos:

 

0 = f(r) = f(x+h) = f(x) + hf'(x) + O(h²)  (30)

 

en donde h=r-x. Si x está próximo a r (es decir hes pequeña), es razonable ignorar el término O(h²):

 

0 = f(x) + hf'(x)  (31)

 

por lo que obtenemos la siguiente expresión para h:

$$h = -\frac{f(x)}{f'(x)}$$ (32)

 

A partir de la ecuación (32) y teniendo en cuenta que r=x+h es fácil derivar la ecuación (29).
 
 

   

Figure: Interpretación geométrica del método de Newton.

[scale=0.9]eps/new-1

  

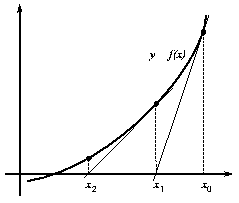
El método de Newton tiene una interpretación geométrica sencilla, como se puede apreciar del análisis de la figura (6). De hecho, el método de Newton consiste en una linealización de la función, es decir, f se reemplaza por una recta tal que contiene al punto (x₀,f(x₀)) y cuya pendiente coincide con la derivada de la función en el punto, f'(x₀). La nueva aproximación a la raíz, x₁, se obtiene de la intersección de la función linear con el eje X de ordenadas.

Veamos como podemos obtener la ecuación (29) a partir de lo dicho en el párrafo anterior. La ecuación de la recta que pasa por el punto (x₀,f(x₀)) y de pendiente f'(x₀) es:

 

y - f(x₀) = f'(x₀)(x-x₀)  (33)

 

de donde, haciendo y=0 y despejando x obtenemos la ecuación de Newton-Raphson (29).
 
 

   

Figure: Dos situaciones en las que el método de Newton no funciona adecuadamente: (a) el método no alcanza la convergencia y (b) el método converge hacia un punto que no es un cero de la ecuación.

[scale=0.9]eps/new-2

  

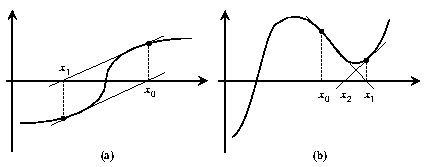
El método de Newton es muy rápido y eficiente ya que la convergencia es de tipo cuadrático (el número de cifras significativas se duplica en cada iteración). Sin embargo, la convergencia depende en gran medida de la forma que adopta la función en las proximidades del punto de iteración. En la figura (7) se muestran dos situaciones en las que este método no es capaz de alcanzar la convergencia (figura (7a)) o bien converge hacia un punto que no es un cero de la ecuación (figura (7b)).

1998-05-11