4.5 Método de Steffensen  4. Cálculo de raíces  4.3 Método de Newton

   
4.4 Método de la secante

El principal inconveniente del método de Newton estriba en que requiere conocer el valor de la primera derivada de la función en el punto. Sin embargo, la forma funcional de f(x) dificulta en ocasiones el cálculo de la derivada. En estos casos es más útil emplear el método de la secante.

El método de la secante parte de dos puntos (y no sólo uno como el método de Newton) y estima la tangente (es decir, la pendiente de la recta) por una aproximación de acuerdo con la expresión:

$$f'(x_{0}) = \frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}$$ (34)

 

Sustituyendo esta expresión en la ecuación (29) del método de Newton, obtenemos la expresión del método de la secante que nos proporciona el siguiente punto de iteración:

$$x_{2} = x_{0} - \frac{x_{1}-x_{0}}{f(x_{1})-f(x_{0})}f(x_{0})$$ (35)

  
 
     

Figure: Representación geométrica del método de la secante.

[scale=0.9]eps/secante

  

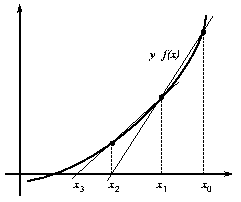
En la siguiente iteración, emplearemos los puntos x₁ y x₂para estimar un nuevo punto más próximo a la raíz de acuerdo con la ecuación (35). En la figura (8) se representa geométricamente este método.

En general, el método de la secante presenta las mismas ventajas y limitaciones que el método de Newton-Raphson explicado anteriormente.

1998-05-11