5. Puntos fijos e iteración funcional

El método de Newton y el de Steffenson son ejemplos de procedimientos mediante los cuales se calcula una sucesión de puntos empleando una fórmula de recurrencia como la siguiente:

 

$$(n \geq 0)$$ x_n+1 = F(x_n) (37)

El algoritmo definido de este modo se denomina iteración funcional.

Ejemplo: En el caso del método de Newton, la expresión (37) se escribiría del modo:

$$F(x) = x - \frac{f(x)}{f'(x)}$$

en tanto que para el método de Steffensen resulta ser:

$$F(x) = x - \frac{[f(x)]^{2}}{f(x+f(x)) - f(x)}$$

La fórmula (37) puede utilizarse para generar sucesiones que no convergen, como por ejemplo la sucesión 1, 3, 9, 27,..., que se obtiene con x₀=1 y F(x)=3x. Sin embargo, estamos interesados en aquellos casos para los que existe $\lim_{n \rightarrow \infty} x_{n}$. Es decir, aquellos casos para los que se cumple:

$$\lim_{n \rightarrow \infty} x_{n} = s$$

Es fácil comprobar que si F es continua se cumple la siguiente relación entre F y s:

$$F(s) = F(\lim_{n \rightarrow \infty} x_{n}) = \lim_{n \rightarrow \infty} F(x_{n}) = \lim_{n \rightarrow \infty} x_{n+1} = s$$

Tenemos, por tanto, que F(s)=s y denominamos a s punto fijo de la función F. Podemos considerar al punto fijo como un valor al que se fija la función durante el proceso iterativo.

Como hemos visto en el apartado anterior, con frecuencia un problema matemático puede reducirse al problema de encontrar un punto fijo de una función. En este caso, nos limitaremos a analizar el caso más sencillo en que F envía en sí mismo algún conjunto cerrado $C \subset \mathbb{R}$ y además se trata de una aplicación contractiva. Se dice que una transformación es contractiva si existe un número $\lambda$ menor que 1 que satisfaga la relación:

$$\vert F(x) - F(y)\vert \leq \lambda\vert x - y\vert$$ (38)

para todos los puntos x e y en el dominio de F.

Las aplicaciones contractivas cumplen una propiedad de gran importancia, que se puede expresar del siguiente modo:

Sea F una aplicación contractiva que va de un conjunto cerrado $C \subset \mathbb{R}$ a C. Entonces F tiene un punto fijo. Más aún, este punto fijo es el límite de toda sucesión que se obtenga a partir de la ecuación (37) con cualquier punto inicial $x_{0} \in C$.

El enunciado anterior, conocido como teorema de la aplicación contractiva se puede demostrar fácilmente. Para ello, primero escribimos x_n en la forma:

$$x_{n} = x_{0}+(x_{1}-x_{0})+(x_{2}-x_{1})+\cdots+(x_{n}-x_{n-1})$$

De acuerdo con la expresión anterior, vemos que la sucesión [x_n]converge si y sólo si la serie

$$\sum_{n=1}^{\infty}(x_{n}-x_{n-1})$$

converge. Para demostrar que esta serie converge, basta con demostrar que la serie

$$\sum_{n=1}^{\infty}\vert x_{n}-x_{n-1}\vert$$ (39)

converge.

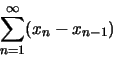
Por otra parte, usando la propiedad de las aplicaciones contractivas expresada por (38) junto con la ecuación (37), podemos escribir:

$$\vert x_{n} - x_{n-1}\vert = \vert F(x_{n-1}) - F(x_{n-2})\vert \leq \lambda\vert x_{n-1} - x_{n-2}\vert$$ (40)

La relación expresada por (40) puede repetirse para obtener:

$$\vert x_{n}-x_{n-1}\vert \leq \lambda\vert x_{n-1}-x_{n-2}\ve... ...-3}\vert \leq \cdots \leq \lambda^{n-1}\vert x_{1}-x_{0}\vert$$ (41)

Para comprobar que la sucesión (39) converge, podemos utilizar el criterio de comparación, de modo que a partir de la expresión (41) obtenemos:

$$\sum_{n=1}^{\infty}\vert x_{n}-x_{n-1}\vert \leq \sum_{n=1}^{... ...t x_{1}-x_{0}\vert = \frac{1}{1-\lambda}\vert x_{1}-x_{0}\vert$$

Es decir, la sucesión converge tal como establece el teorema de la aplicación contractiva expresado anteriormente.

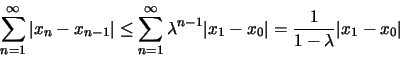
Comprobemos ahora que el punto fijo es efectivamente único. Para ello, supongamos que existen dos puntos fijos, x e y. De acuerdo con la relación (38), tenemos:

$$\vert x-y\vert = \vert F(x)-F(y)\vert \leq \lambda\vert x-y\vert$$

Ya que $\lambda$ es un número finito menor que uno, la única forma de que la ecuación anterior se cumpla es si |x-y| = 0; es decir, si el punto fijo es único.

Ejemplo: Demuestre que la sucesión [x_n] definida recursivamente de acuerdo con:

$$\left\{ \begin{array}{ll} x_{0} = -15 & \\ x_{n+1} = 3 - \frac{1}{2}\vert x_{n}\vert & (n \geq 0) \end{array}\right.$$

es contractiva y tiene un punto fijo.

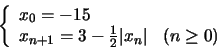
Para comprobar que la función anterior es contractiva, calculemos la diferencia entre dos términos cualesquiera de la sucesión anterior:

$$\left\vert F(x)-F(y) \right\vert = \left\vert (3-\frac{1}{2}\... ...x\vert \right\vert \leq \frac{1}{2} \left\vert y-x \right\vert$$

(por la desigualdad triangular). Por tanto, de acuerdo con el teorema de la aplicación contractiva, la sucesión debe converger a un único punto fijo, cuyo valor es 2 (compruébelo).