5. Puntos fijos e  4. Cálculo de raíces  4.5 Método de Steffensen

   
4.6 Método de la falsa posición

El método de la falsa posición pretende conjugar la seguridad del método de la bisección con la rapidez del método de la secante. Este método, como en el método de la bisección, parte de dos puntos que rodean a la raíz f(x) = 0, es decir, dos puntos x₀ y x₁tales que f(x₀)f(x₁) < 0. La siguiente aproximación, x₂, se calcula como la intersección con el eje X de la recta que une ambos puntos (empleando la ecuación (35) del método de la secante). La asignación del nuevo intervalo de búsqueda se realiza como en el método de la bisección: entre ambos intervalos, [x₀,x₂] y [x₂,x₁], se toma aquel que cumpla f(x)f(x₂) < 0. En la figura (9) se representa geométricamente este método.
 
     

Figure: Representación geométrica del método de la falsa posición.

[scale=0.9]eps/falpos

  

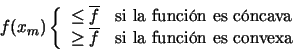
La elección guiada del intervalo representa una ventaja respecto al método de la secante ya que inhibe la posibilidad de una divergencia del método. Por otra parte y respecto al método de la bisección, mejora notablemente la elección del intervalo (ya que no se limita a partir el intervalo por la mitad).
 
 

   

Figure: Modificación del método de la falsa posición propuesta por Hamming. La aproximación a la raíz se toma a partir del punto de intersección con el eje X de la recta que une los puntos ( x₀,f(x₀)/2) y (x₁,f(x₁)) si la función es convexa en el intervalo (figura a) o bien a partir de la recta que une los puntos (x₀,f(x₀)) y (x₁, f(x₁)/2) si la función es cóncava en el intervalo (figura b).

[scale=0.9]eps/hamming

  

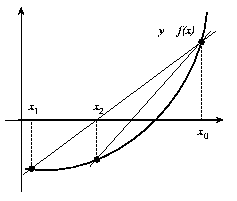
Sin embargo, el método de la falsa posición tiene una convergencia muy lenta hacia la solución. Efectivamente, una vez iniciado el proceso iterativo, uno de los extremos del intervalo tiende a no modificarse (ver figura (9)). Para obviar este problema, se ha propuesto una modificación del método, denominada método de Hamming. Según este método, la aproximación a una raíz se encuentra a partir de la determinación del punto de intersección con el eje X de la recta que une los puntos ( x₀,f(x₀)/2) y (x₁,f(x₁)) si la función es convexa en el intervalo o bien a partir de la recta que une los puntos (x₀,f(x₀)) y (x₁, f(x₁)/2) si la función es cóncava en el intervalo. En la figura (10) se representa gráficamente el método de Hamming.

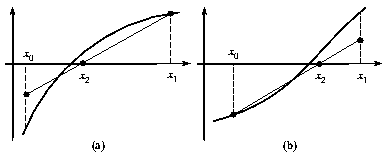
Como hemos comentado, el método de Hamming requiere determinar la concavidad o convexidad de la función en el intervalo de iteración. Un método relativamente sencillo para determinar la curvatura de la función consiste en evaluar la función en el punto medio del intervalo, f(x_m) (en donde x_m se calcula como en el método de la bisección) y comparar este valor con la media de los valores de la función en los extremos del intervalo, $\overline{f} = (f(x_{0}) +f(x_{1}))/2$. Tenemos entonces que:

$$f(x_{m}) \left\{\begin{array}{ll}\leq \overline{f} & \mbo......line{f} & \mbox{si la función es convexa}\end{array} \right.$$  

1998-05-11