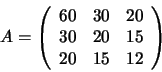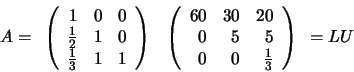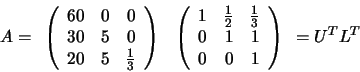Next: 6.1.3 Eliminación gaussiana básica
Up: 6.1 Métodos de resolución
Previous: 6.1.1 Sistemas fáciles de
Supongamos que A se puede factorizar como el producto de una matriz
triangular inferior L con una matriz triangular superior U:
En este caso, el sistema de ecuaciones dado por (44)
podría representarse en la forma:
Si denominamos z a la matriz columna de n filas resultado del
producto de las matrices Ux, tenemos que la
ecuación (52) se puede reescribir del siguiente modo:
A partir de las ecuaciones (52) y (53), es
posible plantear un algoritmo para resolver el sistema de ecuaciones
empleando dos etapas:
- Primero obtenemos z aplicando el algoritmo de
sustitución progresiva en la ecuación (53).
- Posteriormente obtenemos los valores de x aplicando el
algoritmo de sustitución regresiva a la ecuación
Ux = z
El análisis anterior nos muestra lo fácil que es resolver estos dos
sistemas de ecuaciones triangulares y lo útil que resultaría
disponer de un método que nos permitiera llevar a cabo la
factorización A=LU. Si disponemos de una matriz A de
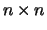 ,
estamos interesados en encontrar aquellas matrices:
,
estamos interesados en encontrar aquellas matrices:
tales que cumplan la ecuación (51). Cuando esto es
posible, decimos que A tiene una descomposición LU. Se
puede ver que las ecuación anterior no determina de forma única a Ly a U. De hecho, para cada i podemos asignar un valor distinto de
cero a lii o uii (aunque no ambos). Por ejemplo, una
elección simple es fijar lii=1 para
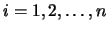 haciendo de
esto modo que L sea una matriz triangular inferior
unitaria. Otra elección es hacer U una matriz triangular
superior unitaria (tomando uii=1 para cada i).
haciendo de
esto modo que L sea una matriz triangular inferior
unitaria. Otra elección es hacer U una matriz triangular
superior unitaria (tomando uii=1 para cada i).
Para deducir un algoritmo que nos permita la factorización LU de Apartiremos de la fórmula para la multiplicación de matrices:
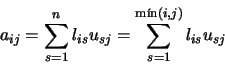 |
(54) |
en donde nos hemos valido del hecho de que lis=0 para s >i y
usj=0 para s>j.
En este proceso, cada paso determina una nueva fila de U y una nueva
columna de L. En el paso k, podemos suponer que ya se calcularon
las filas
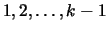 de U, al igual que las columnas
de U, al igual que las columnas
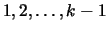 de L. Haciendo i=j=k en la ecuación (54)
obtenemos
de L. Haciendo i=j=k en la ecuación (54)
obtenemos
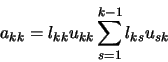 |
(55) |
Si especificamos un valor para lkk (o para ukk), a partir de
la ecuación (55) es posible determinar un valor para
el otro término. Conocidas ukk y lkk y a partir de la
ecuación (54) podemos escribir las expresiones para la
k-ésima fila (i=k) y para la k-ésima columna (j=k),
respectivamente:
Es decir, las ecuaciones (57) se pueden emplear para
encontrar los elementos ukj y lik.
El algoritmo basado en el análisis anterior se denomina
factorización de Doolittle cuando se toman los términos
lii = 1 para
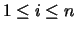 (L triangular inferior unitaria)
y factorización de Crout cuando se toman los términos
uii=1 (U triangular superior unitaria).
(L triangular inferior unitaria)
y factorización de Crout cuando se toman los términos
uii=1 (U triangular superior unitaria).
Una implementación en pseudocódigo del algoritmo para llevar a
cabo la factorización LU se muestra en la figura (11).
Figure:
Implementación del algoritmo de la factorización LU.
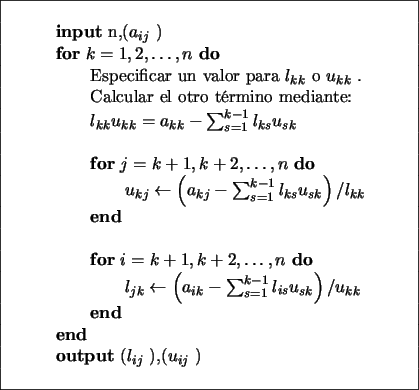 |
Es interesante notar que los bucles que permiten el cómputo de la
k-ésima fila de U y de la k-ésima columna de L se pueden
llevar a cabo en paralelo, es decir, pueden evaluarse simultáneamente
sobre dos procesadores, lo que redunda en un importante ahorro del
tiempo de cálculo.
Ejemplo: Encuentre las factorizaciones de Doolittle y Crout de la
matriz:
La factorización de Doolittle es, a partir del algoritmo:
En vez de calcular la factorización de Crout directamente, la podemos
obtener a partir de la factorización de Doolittle que acabamos de ver.
Efectivamente, si tenemos en cuenta que la matriz A es simétrica, es
posible comprobar que se cumple la relación:
A = LU = UTLT
por lo que la factorización de Crout resulta ser:



Next: 6.1.3 Eliminación gaussiana básica
Up: 6.1 Métodos de resolución
Previous: 6.1.1 Sistemas fáciles de
Wladimiro Diaz Villanueva
1998-05-11
![]() ,
estamos interesados en encontrar aquellas matrices:
,
estamos interesados en encontrar aquellas matrices:
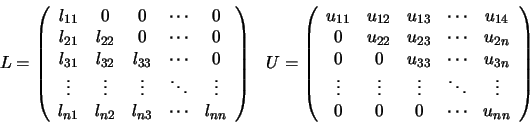
![]() de U, al igual que las columnas
de U, al igual que las columnas
![]() de L. Haciendo i=j=k en la ecuación (54)
obtenemos
de L. Haciendo i=j=k en la ecuación (54)
obtenemos
![]() (L triangular inferior unitaria)
y factorización de Crout cuando se toman los términos
uii=1 (U triangular superior unitaria).
(L triangular inferior unitaria)
y factorización de Crout cuando se toman los términos
uii=1 (U triangular superior unitaria).