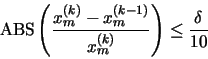Next: 6.2.2 Método de Richardson
Up: 6.2 Métodos iterativos
Previous: 6.2 Métodos iterativos
En general, en todos los procesos iterativos para resolver el sistema
Ax=b se recurre a una cierta matriz Q, llamada matriz
descomposición, escogida de tal forma que el problema
original adopte la forma equivalente:
La ecuación (62) sugiere un proceso iterativo que se
concreta al escribir:
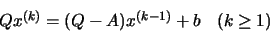 |
(63) |
El vector inicial x(0) puede ser arbitrario, aunque si se dispone
de un buen candidato como solución éste es el que se debe emplear.
La aproximación inicial que se adopta, a no ser que se disponga de una
mejor, es la idénticamente nula
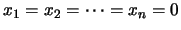 .
A
partir de la ecuación (63) se puede calcular una sucesión
de vectores x(1), x(2), .... Nuestro objetivo es escoger
una matriz Q de manera que:
.
A
partir de la ecuación (63) se puede calcular una sucesión
de vectores x(1), x(2), .... Nuestro objetivo es escoger
una matriz Q de manera que:
- se pueda calcular fácilmente la sucesión [x(k)].
- la sucesión [x(k)] converja rápidamente a la solución.
Como en todo método iterativo, deberemos especificar un criterio de
convergencia 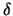 y un número máximo de iteraciones M, para
asegurar que el proceso se detiene si no se alcanza la convergencia.
En este caso, puesto que x es un vector, emplearemos dos criterios
de convergencia que se deberán satisfacer simultáneamente:
y un número máximo de iteraciones M, para
asegurar que el proceso se detiene si no se alcanza la convergencia.
En este caso, puesto que x es un vector, emplearemos dos criterios
de convergencia que se deberán satisfacer simultáneamente:
- 1.
- El módulo del vector diferencia,
 ,
partido por el módulo del vector x,
,
partido por el módulo del vector x,
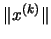 deberá ser menor
que la convergencia deseada:
deberá ser menor
que la convergencia deseada:
- 2.
- La diferencia relativa del mayor elemento en valor absoluto del
vector x(k),
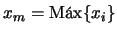 ,
deberá ser diez veces
menor que
,
deberá ser diez veces
menor que 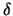 :
:



Next: 6.2.2 Método de Richardson
Up: 6.2 Métodos iterativos
Previous: 6.2 Métodos iterativos
Wladimiro Diaz Villanueva
1998-05-11
![]() y un número máximo de iteraciones M, para
asegurar que el proceso se detiene si no se alcanza la convergencia.
En este caso, puesto que x es un vector, emplearemos dos criterios
de convergencia que se deberán satisfacer simultáneamente:
y un número máximo de iteraciones M, para
asegurar que el proceso se detiene si no se alcanza la convergencia.
En este caso, puesto que x es un vector, emplearemos dos criterios
de convergencia que se deberán satisfacer simultáneamente: