Next: 2.4.5 Figuras Up: 2.4 Flujo Compresible Unidimensional Previous: 2.4.3 Ondas Simples
![]() En el estado definido por laonda simple
En el estado definido por laonda simple![]() de compresión
los valores de la presión y la velocidadpermanecen constantes a lo largo de
las características
de compresión
los valores de la presión y la velocidadpermanecen constantes a lo largo de
las características![]()
![]() En los puntos en que las características se cruzan la solución
es discontinua
En los puntos en que las características se cruzan la solución
es discontinua
![]() CHOQUE
CHOQUE
![]() Flujo unidimensional, ecuaciones en forma conservativa:
Flujo unidimensional, ecuaciones en forma conservativa:
| (33) |
| (34) |
| (35) |
![\fbox{\parbox[b]{3.5in}{
{\bf Sistema de leyes de conservaci\'on:}
\begin{displa...
...l t}
+ \frac{\partial {\bf F(U)}}{\partial x} = 0
}
\end{displaymath}}}](img255.png)
![]() Si el campo vectorial
Si el campo vectorial![]() se anula en el infinito:
se anula en el infinito:
| (36) |
![]() Sea
Sea ![]() la trayectoria de la discontinuidad:
la trayectoria de la discontinuidad:
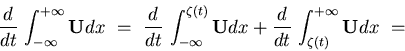 |
(37) |
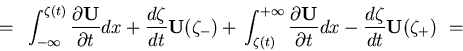 |
(38) |
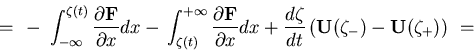 |
(39) |
| (40) |
![\fbox{\parbox[b]{4.5in}{
{\bf Condiciones de salto:}
\begin{displaymath}
\displa...
... \Longrightarrow
[{\bf F}]
=
v_s [{\bf U}]
\end{displaymath}}}](img264.png)
![]()
![]() es el salto a través de la discontinuidad
es el salto a través de la discontinuidad
![]()
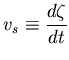 es la velocidad de propagación de
la discontinuidad
es la velocidad de propagación de
la discontinuidad
![\fbox{\parbox[b]{4.0in}{
{\bf Relaciones de Rankine-Hugoniot:}
\begin{displaymat...
...,
v_s [\rho (\displaystyle{\frac{1}{2} v^{2} + \epsilon)]}
\end{displaymath}}}](img267.png)
![]() Sistema de referencia ligado a la discontinuidad
Sistema de referencia ligado a la discontinuidad
![]()
![]() es la velocidad relativa del fluido
es la velocidad relativa del fluido
![\fbox{\parbox[b]{6.0in}{
\begin{displaymath}[\rho u] = 0
\Longright...
..._1 }
=
\displaystyle{\frac{1}{2} u_2^{2} + h_2 }
\end{displaymath}}}](img269.png)
![]() El estado con subíndice
El estado con subíndice ![]() es el delantero (trasero)
o prechoque (postchoque).
es el delantero (trasero)
o prechoque (postchoque).
![]() La cantidad
La cantidad![]() es el flujo de masaa través de la discontinuidad.
es el flujo de masaa través de la discontinuidad.
![]() Las relaciones de salto no determinan completamente el sistema (condición de
entropía).
Las relaciones de salto no determinan completamente el sistema (condición de
entropía).
![]() Definiendo
Definiendo
![]() (volumen específico), las condiciones de
salto se pueden reescribir:
(volumen específico), las condiciones de
salto se pueden reescribir:
![]() La (2.4.4) es definida positiva
La (2.4.4) es definida positiva
![]() A través de la onda de choque, en principio son válidas las dos
combinaciones de relaciones siguientes: a)
A través de la onda de choque, en principio son válidas las dos
combinaciones de relaciones siguientes: a) ![]() ,
,
![]() , b)
, b)
![]() ,
,
![]()
![]() La condición de entropía selecciona la a)
La condición de entropía selecciona la a)
![]() De (2.4.4)
De (2.4.4)
![]() .
.
![]() La (2.4.4) es la adiabática de Hugoniot.
La (2.4.4) es la adiabática de Hugoniot.
![]() La adiabática de Hugoniot (2.4.4) relaciona las variables termodinámicas a ambos lados de
la onda de choque. Junto con la ecuación de estado
La adiabática de Hugoniot (2.4.4) relaciona las variables termodinámicas a ambos lados de
la onda de choque. Junto con la ecuación de estado
![]() , y fijado el
estado
, y fijado el
estado ![]() , la (2.4.4) admite una representación en el plano
, la (2.4.4) admite una representación en el plano ![]() :
lugar geométrico de todos los estados 2 que pueden ser conectados con el 1 a través de una
onda de choque , la cual tiene al estado 1 como prechoque.
:
lugar geométrico de todos los estados 2 que pueden ser conectados con el 1 a través de una
onda de choque , la cual tiene al estado 1 como prechoque.
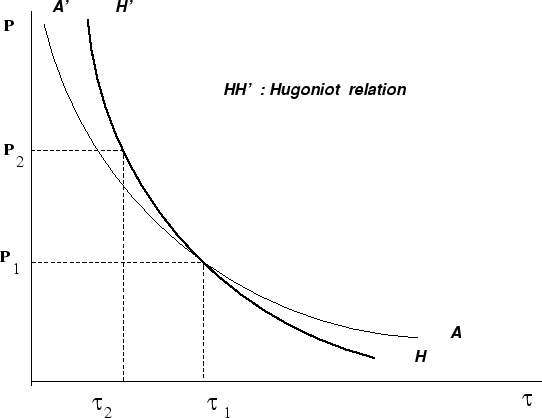 |
Algunas consecuencias de las condiciones de salto(2.4.4),(2.4.4) y (2.4.4):
![]()
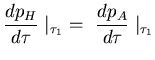
![]()
![]()
![]() En la adiabática de Hugoniot, sean los estados
En la adiabática de Hugoniot, sean los estados ![]() y
y ![]() :
:
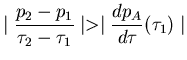
![]() De (2.4.4):
De (2.4.4):
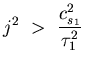
![]()
![]() De (2.4.4):
De (2.4.4):
![]()
![]() El estado prechoque, en el s.d.r. de la onda de choque, es supersónico.
El estado prechoque, en el s.d.r. de la onda de choque, es supersónico.
Discontinuidad de contacto: No hay flujo de masa
![\fbox{\parbox[b]{5.0in}{
{\bf Condiciones de salto :}
\begin{displaymath}[v] ...
... , [p] = 0 ,
[\rho] arbitrario
\end{displaymath}}}](img290.png)