4.1.2 Exact solution of a Riemann problem

• Self-similar solution: $$\xi=\frac{x-x_0}{t}$$

• 5 regions, 3 elementary waves

• State 1: initial left state (with respect to $x_0$) $x_1=x_0+\xi_1 t$ ($\xi_1<0$)

• State 2: rarefaction $v=v_2(\xi), \rho=\rho_2((\xi), p=p_2(\xi)$, $x_2=x_0+\xi_2 t$

• States 3 and 4: constant states separated by a contact discontinuity, $x_3=x_0+\xi_3 t$

• State 5: initial right state. Its leftmost part is limited by the shock wave moving with speed $\xi_4$

• Unknowns: $v_3, p_3, \rho_3, v_4, p_4, \rho_4$ (constants), $v_2(\xi), p_2(\xi), \rho_2(\xi)$ (functions) and $\xi_1, \xi_2, \xi_3, \xi_4$ (velocity of points separating the regions)

• Solution procedure:

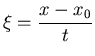
  First: the RH conditions accross discontinuities provide 6 equations to solve for 6 variables

  Second: the rest of relations are obtained from the condition of self-similar flow accross the rarefaction wave

SRH equations (Cartesian coordinates, planar symmetry):

$$\begin{eqnarray*} \frac{\partial(\rho W)}{\partial t} + \frac{\partial(\rho W v... ...)}{\partial t} + \frac{\partial(\rho h W^2 v)}{\partial x} &=& 0 \end{eqnarray*}$$

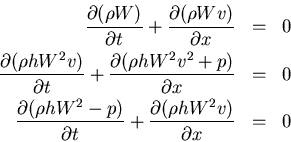
self-similarity ( 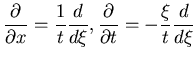$$\frac{\partial}{\partial x}=\frac{1}{t}\frac{d}{d\xi}, \frac{\partial}{\partial t} = -\frac{\xi}{t}\frac{d}{d\xi}$$) and some algebra lead to

$$\begin{eqnarray*} (v-\xi)\frac{d\rho}{d\xi} + (1-v\xi)\rho W^2 \frac{dv}{d\xi} &... ...-\xi)W^2 \rho h \frac{dv}{d\xi} + (1-v\xi) \frac{dp}{d\xi} &=& 0 \end{eqnarray*}$$

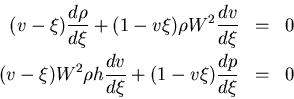
A self-similar flow is isentropic: $$\frac{dp}{d\xi} = c_s^2 h \frac{d\rho}{d\xi}$$

$$\begin{eqnarray*} (v-\xi)\frac{d\rho}{d\xi} + (1-v\xi)\rho W^2 \frac{dv}{d\xi} &... ...ho W^2 \frac{dv}{d\xi} + (1-v\xi) c_s^2 \frac{d\rho}{d\xi} &=& 0 \end{eqnarray*}$$

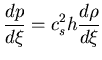
whose solution is $\begin{array}{\vert c\vert}\hline \displaystyle \xi=\frac{v\mp c_s}{1\mp v c_s} \hspace{1cm} (\dagger) \hline \end{array}$

$v_1=0 \rightarrow \xi_1=-c_{s_1}$

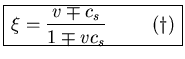
In Eq. ($\ast$) $$\rightarrow W^2 dv = -\frac{c_s}{\rho} d\rho$$

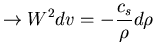
$$\begin{eqnarray*} \frac{1}{2}\left[\ln\frac{1+v}{1-v}\right]_{v_1}^{v} = -\displaystyle\int_{\rho_1}^{\rho}\frac{c_s}{\rho}d\rho \end{eqnarray*}$$

Adiabatic flow: $p=K\rho^{\gamma}$, $$c_s^2=\frac{\gamma (\gamma-1) p} {\rho(\gamma-1) + \gamma p}$$

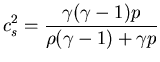
Hence, two arbitrary states are related according to: $$\rho=\rho_1\left[\frac{c_s^2(\gamma-1-c^2_{s_1})}{c^2_{s_1} (\gamma-1-c^2_{s})} \right]^{\frac{1}{\gamma-1}}$$

$$\begin{eqnarray*} \rightarrow \frac{1}{2}\left[\ln\frac{1+v}{1-v}\right]_{v_1}^{... ...mma,c_{s_1},v_1,v) \hspace{1cm} (\ddagger) \hline \end{array}\end{eqnarray*}$$

Solving Eqs. ($\dagger$) and ($\ddagger$) allows to obtain $v(x,t)$ and $c_s(x,t)$ in state 2, and hence $\rho$ and $p$

Finally, the continuity of the flow guarantees: $v_3=v(\xi_2), p_3=p(\xi_2)$ and $\rho_3=\rho(\xi_2)$