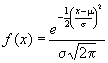DISTRIBUCIÓN NORMAL
(ir a distribucción normal desarrollada)

ir a script de la normal

La distribución normal es la más importante de todas las distribuciones de probabilidad.Es una distribución de variable continua con campo de variación [-¥ ,¥ ], que queda especificada a través de dos parámetros ( que acaban siendo la media y la desviación típica de la distribución).

Una variable aleatoria continua, X, definida en [-¥ ,¥ ] seguirá una distribución normal de parámetros m y s , ( X ~ N(m ; s ) ) , si su función de densidad es :

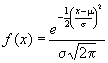para x Î [-¥ ,¥ ]

cuya representación gráfica es:

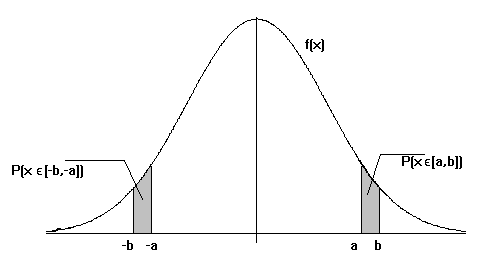
Importancia de la distribución Normal.

a) Enorme número de fenómenos que puede modelizar: Casi todas las características cuantitativas de las poblaciones muy grades tienden a aproximar su distribución a una distribución normal.

b) Muchas de las demás distribuciones de uso frecuente, tienden a distribuirse según una Normal, bajo ciertas condiciones.

c) (En virtud del teorema central del límite).Todas aquellas variables que pueden considerarse causadas por un gran número de pequeños efectos (como pueden ser los errores de medida) tienden a distribuirse según una distribución normal.

La probabilidad de cualquier intervalo se calcularía integrando la función de densidad a lo largo de ese de intervalo, pero no es necesario nunca resolver la integral pues existen tablas que nos evitan este problema.

F.G.M.: puede probarse que la función generatriz de momentos de una distribución N(m ; s ) es:

                                                                        f (t) = E(e^tx) = e(^{m t + ½ s2t2})

A partir de ella es fácil comprobar como efectivamente la media de la distribución es el parámetro m y, cómo su varianza es el parámetro s .

Igualmente puede comprobarse que la distribución es simétrica y que su curtósis es nula.

Propiedad importante: "CUALQUIER TRANSFORMACIÓN LINEAL DE UNA VARIABLE ALEATORIA NORMAL TIENE TAMBIÉN UNA DISTRIBUCIÓN NORMAL DONDE LA MEDIA DE LA NUEVA VARIABLE ES LA MISMA TRANSFORMACIÓN LINEAL DE LA MEDIA DE LA ANTIGUA Y DONDE LA DESVIACIÓN TÍPICA ES LA DESVIACIÓN TÍPICA ANTIGUA MULTIPLICADA POR EL COEFICIENTE ANGULAR DE LA TRANSFORMACIÓN":

Dada una variable X ~ N(m ; s ) si la nueva variable Y es Y = a+bX

Y~ N(a+bm ; bs ) :

en efecto: la F.G.M de la distribución de X será:

E(e^tx) = e(^{m t + ½ s2t2})

y la F.G.M. de la distribución de Y será:

fy(t)= e^at.f_x(bt) = e^at .e(^{m bt + ½ s2b2t2}) = e(^(a+bm )t + (bs )²t²)

que es la F.G.M de una distribución N(a+bm ; bs ) //*q.e.d.*//

Consecuencia importante de esto es que si se tipifica una variable X / X ~ N(m ; s ) la nueva variable Z = tendrá una distribución N(0,1).

La distribución N(0,1) se conoce con el nombre de Normal tipificada o reducida y tiene una importancia teórica y práctica fundamental.Su Función de distribución está tabulada y ello nos permite calcular directamente cualquier probabilidad de cualquier intervalo de cualquier distribución normal ( X ~ N(m ; s )), sin necesidad de integrar.

En efecto: si X ~ N(m ; s ) y queremos calcular P(XÎ [a,b])==P(a£ X £ b) =

donde F es la F. de distribución de una Normal tipificada, que puede evaluarse a través de las tablas.

ir a modelos de probabilidad