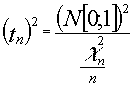es
decir una chi2 con m grados de libertad es
decir una chi2 con m grados de libertad
es
decir una chi2 con n grados de libertad ;
de manera que si establecemos el cociente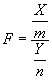 
, es decir el cociente entre ambas chi2 divididas a su vez, por sus correspondientes grados de
libertad tendremos que la función F corresponde a una distribución F de Snedecor con m y
n grados de libertad ; es decir una 
Queda claro por tanto que la distribución F de Snedecor tiene dos parámetros , que son m y n ; grados de libertad del numerador , grados de libertad del denominador.
Dado que se trata de un cociente entre dos chi2 su forma (gráfica de la función de densidad)será parecida a la de ésta distribución , por lo que estará sólo definida para el campo positivo de la variable y su apariencia variará según los grados de libertad ; estando más próxima la densidad de probabilidad a los valores próximos a cero de la variable , cuando los grados de libertad ( sus parámetros) sean bajos.
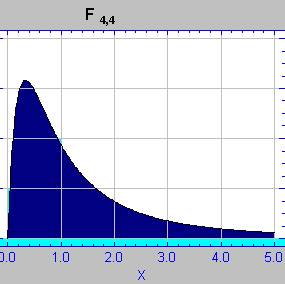
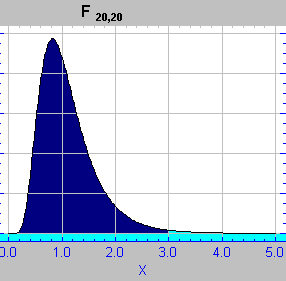
La función de densidad de la F de Snedecor viene dada por
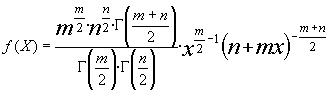
siendo m y n los parámetros de la función(distribución) y 
la función gamma de Euler
la media de la distribución es 
si n > 2 siendo la
varianza cuando n> 4
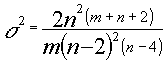
Lógicamente si 
su inversa 
lo que ayuda al cálculo de probabilidades para distintos valores de la
variable mediante la utilización de tablas , caso que no es el nuestro pues estos los realizamos mediante un programa que incluimos , no
obstante ,a modo de ejemplo , plantemos:
Si X 
y nos interesa el
cálculo de 
dicho
resultado es 0,13
Luego 
luego 
Como curiosidad tenemos que una F con un grado de libertad en el numerador y n en el denominador , no es más que el cuadrado de una t de student con n grados de libertadad dado que :
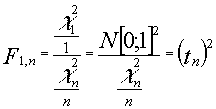dado que :
una 
luego una :
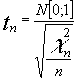siendo una 
una
