Teorema de Bernouilli. (ley débil de los grandes números)
Con el mismo planteamiento que el teorema de Khintchine , es decir ;
Dada una sucesión de variables aleatorias {Xn}
y
estableciendo una nueva variable ![]()
y siendo ,en este caso, las variables que forman la sucesión dicotómicas de parámetro p
El
teorema de Bernouilli plantea que ![]()
o , de otra manera 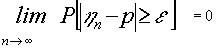
Es decir , que la variable media de la sucesión de dicotómicas de parámetro p converge en probabilidad al parámetro p común a todas ellas
De otro modo podríamos plantear la sucesión
de (n) dicotómicas de parámetro p como una binomial y así:
la sucesión {Xn} sería una B(X, n, p)
donde la variable aleatoria anterior ![]() sería ,
ahora , la razón frecuencial de éxitos o frecuencia relativa del suceso , X/n ; de
esta manera el teorema de Bernouilli nos diría que:
sería ,
ahora , la razón frecuencial de éxitos o frecuencia relativa del suceso , X/n ; de
esta manera el teorema de Bernouilli nos diría que:
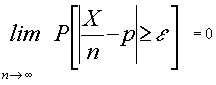
es decir, "la razón frecuencial de éxitos converge en probabilidad a la probabilidad de éxito de una binomial"
Para demostrarlo partimos de la conocida desigualdad de Chebyshev , así:
![]()
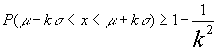 haciendo
haciendo
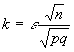
y
dado que conocemos que en la binomial
m
=p·q y ![]()
tendremos que : 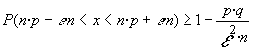
dividiendo por n (los miembros del primer término) y despejando tendríamos:
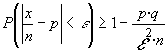 o , lo que
es lo mismo
o , lo que
es lo mismo
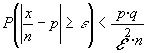 y , dado que el
valor máximo de p·q=0,4
y , dado que el
valor máximo de p·q=0,4
tendremos que:
(1)![]()
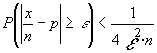 y que evidentemente tiende a 0 cuando n tiende a infinito :
y que evidentemente tiende a 0 cuando n tiende a infinito :
demostrando que ![]()
Como curiosidad ,se ha establecido en (1) una cota de probabilidad que nos permite calcular la probabilidad máxima con la que diferirán en una determinada cantidad la "razón frecuencial de éxitos" y la "probabilidad de éxito" de una binomial .
Así , y como ejemplo , nos planteamos;
Si nos planteamos que la probabilidad sea
inferior a 0,10 , para el hecho de que , al lanzar una moneda con el ánimo de conseguir
caras , la diferencia entre las que han salido y las que debieran haber salido (la mitad)
sea superior al 2% ,
¿Cuántas veces debemos de lanzar la moneda?
Nos planteamos conocer n (número de lanzamientos) , despejando de (1)
Tendremos 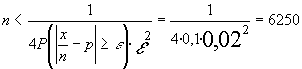 veces lanzaremos para que la diferencia entre el número de caras que han de salir (3125)
y las que verdaderamente saldrán , sea mayor del 2% (mas, menos 125 caras) ,con una
probabilidad inferior a 0,1.
veces lanzaremos para que la diferencia entre el número de caras que han de salir (3125)
y las que verdaderamente saldrán , sea mayor del 2% (mas, menos 125 caras) ,con una
probabilidad inferior a 0,1.
Es conveniente , por último , precisar , que el teorema de Bernouilli demuestra la estabilidad de las frecuencias relativas de éxito entorno a la probabilidad de éxito , no asegurando que sea la verdadera probabilidad de éxito la derivada de las frecuencias relativas de éxito