| Signo del número real x: | 1 bit |
| Signo del exponente m: | 1 bit |
| Exponente (entero |m|): | 7 bits |
| Mantisa (número real |q|): | 23 bits |
Dado que la mantisa siempre se representa normalizada, el primer bit en q es siempre 1, por lo que no es necesario almacenarlo proporcionando un bit significativo adicional. Esta forma de almacenar un número en punto flotante se conoce con el nombre de técnica del 'bit fantasma'.
Se dice que un número real expresado como aparece en la ecuación (18) y que satisface la ecuación (19) tiene la forma de punto flotante normalizado. Si además puede representarse exactamente con |m| ocupando 7 bits y |q| ocupando 24 bits, entonces es un número de máquina en el MARC-323
La restricción de que |m| no requiera más de 7 bits significa que:
Ya que ![]() ,
la MARC-32 puede manejar números tan pequeños como
10-38 y tan grandes como 1038. Este no es un intervalo
de valores suficientemente generoso, por lo que en muchos casos debemos
recurrir a programas escritos en aritmética de doble precisión
e incluso de precisión extendida.
,
la MARC-32 puede manejar números tan pequeños como
10-38 y tan grandes como 1038. Este no es un intervalo
de valores suficientemente generoso, por lo que en muchos casos debemos
recurrir a programas escritos en aritmética de doble precisión
e incluso de precisión extendida.
Como q debe representarse empleando no más de 24 bits
significa que nuestros números de máquina tienen una precisión
limitada cercana a las siete cifras decimales, ya que el bit menos significativo
de la mantisa representa unidades de ![]() .
Por tanto, los números expresados mediante más de siete dígitos
decimales serán objeto de aproximación cuando se almacenen
en el ordenador.
.
Por tanto, los números expresados mediante más de siete dígitos
decimales serán objeto de aproximación cuando se almacenen
en el ordenador.
Por ejemplo: 0.5 representado en punto flotante en el MARC-32 (longitud de palabra de 32 bits) se almacena en la memoria del siguiente modo:
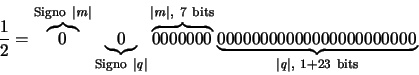
Ejemplo 5: Suponga un ordenador cuya notación de punto fijo consiste
en palabras de longitud 32 bits repartidas del siguiente modo: 1 bit para
el signo, 15 bits para la parte entera y 16 bits para la parte fraccionaria.
Represente los números 26.32, ![]() y 12542.29301 en base 2 empleando esta
notación de punto fijo y notación de punto flotante MARC-32
con 32 bits. Calcule el error de almacenamiento cometido en cada caso.
y 12542.29301 en base 2 empleando esta
notación de punto fijo y notación de punto flotante MARC-32
con 32 bits. Calcule el error de almacenamiento cometido en cada caso.
Solución: El número 26.32 en binario se escribe del siguiente modo:
Empleando las representaciones comentadas, obtenemos:
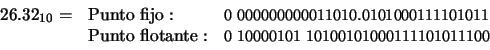
Si expresamos el error como la diferencia entre el valor y el número realmente almacenado en el ordenador, obtenemos:
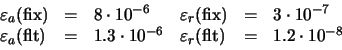
En cuanto a los otros dos números, obtenemos:
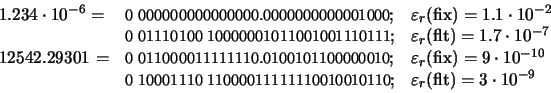
Antes de entrar con detalle en la aritmética de los números
en punto flotante, es interesante notar una propiedad de estos números
de especial importancia en los cálculos numéricos y que hace
referencia a su densidad en la línea real. Supongamos que p,
el número de bits de la mantisa, sea 24. En el intervalo ![]() (exponente f = 0) es posible representar 224 números
igualmente espaciados y separados por una distancia 1/224. De
modo análogo, en cualquier intervalo
(exponente f = 0) es posible representar 224 números
igualmente espaciados y separados por una distancia 1/224. De
modo análogo, en cualquier intervalo ![]() hay 224 números equiespaciados, pero su densidad en este
caso es 2f/224.
Por ejemplo, entre 220
= 1048576 y 221 = 2097152
hay 224 = 16777216 números,
pero el espaciado entre dos números sucesivos es de sólo
hay 224 números equiespaciados, pero su densidad en este
caso es 2f/224.
Por ejemplo, entre 220
= 1048576 y 221 = 2097152
hay 224 = 16777216 números,
pero el espaciado entre dos números sucesivos es de sólo ![]() .
De este hecho se deriva inmediatamente una regla práctica: cuando
es necesario comparar dos números en punto flotante relativamente
grandes, es siempre preferible comparar la diferencia relativa a la magnitud
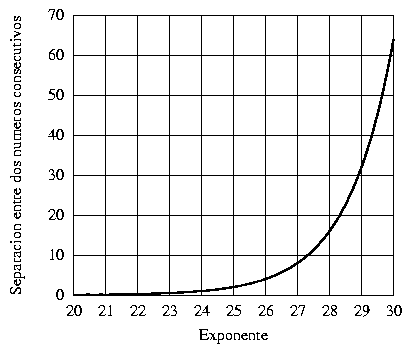
de los números. En la figura (1)
se representa gráficamente la separación entre dos números
consecutivos en función del exponente f en el rango f
= [20,30].
.
De este hecho se deriva inmediatamente una regla práctica: cuando
es necesario comparar dos números en punto flotante relativamente
grandes, es siempre preferible comparar la diferencia relativa a la magnitud
de los números. En la figura (1)
se representa gráficamente la separación entre dos números
consecutivos en función del exponente f en el rango f
= [20,30].
|
|