P1-Difracción de electrones
Introducción
La
naturaleza cuántica de los sistemas físicos, descritos por ondas de
probabilidad, implica una relación entre su longitud de onda λ y su
momento lineal p (medidos en un sistema de referencia dado). Esta
relación, propuesta por Louis De Broglie en 1914, antes de la
formulación de la teoría cuántica, se expresa en la forma:
λ = h/p
[Ec. 1]
siendo h la llamada constante de Planck: h = 6.626 x 10-34 J.s.
Según
esta expresión un electrón (masa del electrón: mc2 = 511 keV) acelerado
por una diferencia de potencial entre 1 y 10 kV, es decir con una
energía cinética entre 1 y 10 keV, a la cual corresponde un momento p
entre 32 y 101 keV/c, tiene una longitud de onda λ entre 0.39 A y 0.12
A. En el caso de fotones estos valores para λ están en el rango de los
rayos X. Por tanto electrones con estas energías podrán exhibir
fenómenos de interferencia análogos a los que presentan los rayos X.
Uno
de los fenómenos ondulatorios más característicos de los rayos X es su
dispersión por cristales (sólidos cristalinos) con distancias
interatómicas comparables a su longitud de onda. Se trata de la
denominada dispersión o difracción de Bragg que analizaremos para su aplicación a electrones.
Dispersión o difracción de Bragg
En
1912, W. Friedrich y P. Knipping, a partir de una sugerencia de M. Von
Laue, hicieron que un haz colimado de rayos X pasase a través de un
cristal detrás del cual se había colocado una placa fotográfica. Además
de un haz central (correspondiente a la dirección incidente) observaron
en la placa una distribución regular de puntos. Este patrón fue
explicado ese mismo año por William Lawrence Bragg por lo que al
fenómeno se le dio el nombre de dispersión o difracción de Bragg.
Este
experimento confirmó dos hipótesis importantes: i) que los rayos X son
una forma de radiación electromagnética y ii) que los átomos de un
cristal están distribuidos en una red regular.
La interferencia de dos rayos puede darse después de
ser dispersados por una serie de planos paralelos en los que se
encuentran los átomos de un cristal. (hay diversas series de planos
paralelos, ver Fig. 2). Dicha interferencia será constructiva (los
rayos estarán en fase, intensidad máxima resultante, punto “brillante”
en la pantalla) en las siguientes condiciones:
- Ambos rayos han de ser dispersados con el mismo
ángulo con el que incidieron (α en la figura 1) independientemente de
la longitud de onda, según la ley de reflexión de las ondas
electromagnéticas.
- Entre los dos rayos dispersados por dos átomos en
planos paralelos (incluyendo el caso del mismo plano) con ángulos
iguales ha de haber una diferencia de caminos recorridos de un número
entero de longitudes de onda, con lo cual, como muestra la figura 1, es
fácil ver que:
2d
sinѲ = n λ
[Ec.
2]
siendo d la distancia interplanar para la serie de
planos considerada, Ѳ = (π/2 - α) y n un número entero
indicador del orden de la interferencia.
La Ec. 2 se conoce como condición de Bragg. Notar
que para el orden dominante, n = 1 y λ dada, cada serie de planos
paralelos, caracterizada por su distancia interplanar, sólo da lugar a
interferencia constructiva (un punto en la pantalla) para un
determinado angulo Ѳ.
| Fig. 1.- Esquema donde se muestra
que para interferencia constructiva entre dos rayos, que son
dispersados por átomos en dos planos atómicos paralelos, la diferencia
de caminos – línea gruesa en color azul – es 2dsinѲ |
Difracción de electrones
Análogamente a los rayos X los electrones pueden
experimentar dispersión de Bragg. Si en vez de un cristal se usa como
dispersor un sólido como el grafito, formado por microcristales con
todas las orientaciones posibles, en la pantalla se observarán anillos
de interferencia constructiva en lugar de puntos. Ello se debe a un
efecto acumulativo: la dispersión por una serie de planos paralelos en
un microcristal producirá, para un orden dado, un punto de
interferencia constructiva en la pantalla; el conjunto de
microcristales orientado simétricamente alrededor del eje determinado
por la dirección del haz inicial dará lugar a la formación de un
anillo. Por tanto por cada serie de planos paralelos (caracterizada por
su distancia interplanar) en un microcristal se tendrá un conjunto de
anillos, un anillo por cada orden de la interferencia.
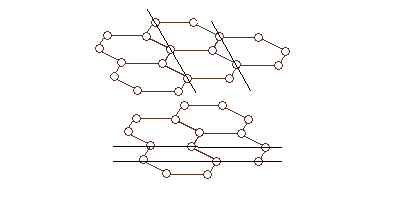 Fig. 2.- Dibujo esquemático de un
conjunto de átomos en un microcristal de grafito. En la distribución
superior se observa una serie deplanos atómicos diferente a la de la
distribución inferior. La distancia entre los dos planos de la
distribución superior es la que llamamos d1, mientras que la de la inferior es d2.
|
Observación experimental: tubo de rayos catódicos
Un Tubo de difracción de electrones es
un tubo de rayos catódicos en el cual electrones producidos
mediante efecto termoiónico, por calentamiento de un filamento, son
acelerados por una diferencia de potencial V y dispersados por una
lámina de grafito. Los electrones salientes viajan por el interior de
una ampolla esférica de vidrio en la que se ha hecho el vacío (para
evitar colisiones de los mismos con moléculas de aire) hasta alcanzar
el extremo de la ampolla en el cual hay una película de un material
fluorescente. Cada impacto electrónico en ésta produce un punto
luminoso por lo que la película juega el papel de pantalla en la que se
proyectará el patrón de difracción.
Fig. 3.- Dibujo esquemático del Tubo de difracción de electrones.
En el laboratorio, el Tubo de difracción se encuentra sujeto a un soporte a través del cual se establecen las conexiones eléctricas a una fuente de alimentación y a un generador de alto voltaje. Para medir la tensión en el generador de alto voltaje mediante un polímetro
estándar se puede disponer de una punta de prueba tal que la lectura en
el polímetro sea de un voltaje 2000 veces menor que el que proporciona
el generador de alto voltaje. Los diámetros de los anillos de difracción se pueden medir con un pie de rey.
Fig. 4.- Montaje de la práctica en el laboratorio
|

