Programa:

• Complementos de Cálculo Diferencial.
• Principios fundamentales de existencia.
• Problemas extremales sin restricciones.
• Problemas extremales para funcionales convexos.
• Problemas extremales con restricciones suaves.
• Desigualdades variacionales.

Objetivos pedagógicos:

La determinación de puntos críticos, eventualmente extremos, de funcionales reales definidos en ciertos espacios de funciones está en la raíz de muchos problemas de economía, mecánica, hidrodinámica, elasticidad, etc.
El cálculo variacional clásico estudia funcionales del tipo




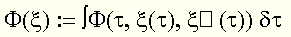
(donde psi pertenece a cierto conjunto admisible de funciones), y muchas de sus generalizaciones. Tiene su origen en determinados problemas físicos planteados en el siglo XVII.
El objetivo del cálculo variacional es el estudio de la posible existencia de extremos de funcionales similares al anterior, así como, en su caso el cálculo efectivo o la aproximación de éstos. Estamos ante una extensa área dentro del Análisis Funcional no Lineal
Los objetivos del curso que nos ocupa son:

• Conocimiento de algunas de las técnicas básicas del tema, que sean accesibles desde los cursos de la licenciatura, con especial hincapié en el Teorema de Euler-Lagrange, y sus pre-requisitos.
• Familiaridad con la resolución de algunos de los ejemplos clásicos (braquistócrona líneas más cortas etc.). Capacidad de modelizar otros problemas físicos sencillos.
• Conocimiento de algunas de las conexiones de los problemas de desigualdades variacionales con otros teoremas de existencia clásicos en Análisis.

Bibliografía recomendada:

• E. Giusti, Direct Methods in the Calculus of Variations, World. Scientific,  2003.
• J. L. Troutman, Variational Calculus with Elementary Convexity,  Springer-Verlag, 1983.
• B. van Brunt,  The calculus of variations. Universitext. Springer-Verlag,  2004.
• E. Zeidler, Applied Functional Análisis, Main Principles and their applicatoions, Col. Applied Mathematical Sciences, vols. 108 y 109, Springer Verlag, 1995.
• E. Zeidler, Nonlinear Functional Analysis and its Applicacions III, Variational Methods and Optimization, Springer Verlag, 1984.

Metodología:

Exposición tradicional, combinada con la realización por parte del alumno de prácticas consistentes fundamentalmente en la resolución de ejercicios temáticos y problemas. 

Criterios de evaluación:

Se valorará la solución por parte de cada uno de los estudiantes de una colección individualizada de ejercicios que entregarán los profesores, así como la exposición oral de alguno de estos ejercicios.