Ejemplos de diseño de un PID

Teniendo el proceso:

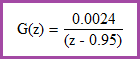Con T = 0.1seg

y con especificaciones:

Te(98%) ≤ 2 seg.

δ ≤ 5%

ep=0%

Siguiendo los pasos vistos en el tema "Reguladores PID":

Paso uno: dibujamos el lugar de las raíces con Scilab:

Dibujado del lugar de las raíces

Paso dos: pasar las especificaciones a discreto:

Te = 4/σ ≈ σ = 2

δ ≤ 5% ≈

Sobreoscilación

ξ = 0.69

arcosξ = Φ

Φ = 46.36

Las especificaciones obtenidas se ven más claramente en el plano S:

Zona de eEspecificaciones en S

Del punto que queremos obtener “s = σ ± w_pj” tenemos ya el “σ” que es igual a 2.

Con un poco de trigonometría básica obtenemos el w_p

w_p= tg(Φ) * σ

w_p= 2.097

Nuestro punto en el plano S es “s = 2 ± 2.097j”

Pasando con el cambio z = e^sT≈ e^-2*0.1 (cos(2.097*0.1) ± sen(2.097*0.1)*j)

z = 0.8 ± 0.17j

Para imaginar un poco como serán las especificaciones en el plano Z, hacemos el modulo de nuestro punto de especificaciones y obtenemos que es 0.81. El tiempo de especificación es circular, mientras que la sobreoscilación es en forma de corazón tumbado. La línea verde es el tiempo de establecimiento, y la roja la sobreoscilación. Y la línea amarilla es la zona que coincide con la zona de especificaciones con el lugar de las raíces.

Corte de especificaciones con lugar de las raíces

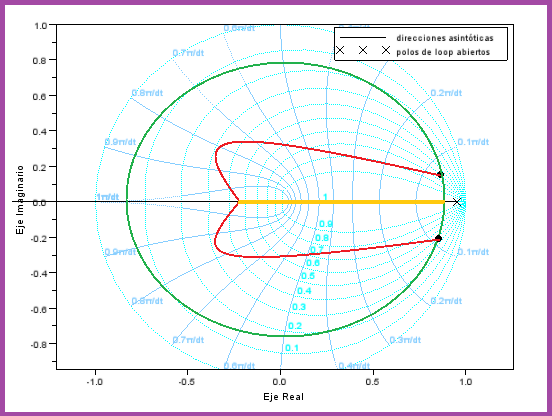Paso tres: seguimos el árbol de decisiones.

Partimos desde la K. Y continuamos hasta la decisión TMR-TS

Como vemos, necesitamos tener un “z-1” por la especificación de tener un error de posición nulo. Pero no tenemos ningún “z-1” en nuestro proceso, así que debemos añadir acción integral, porque la resta del TMR-TS nos da 1.

Como el lugar de las raíces si que se nos corta con nuestra zona de especificaciones, no añadimos parte D. Como vemos se ha seguido el siguiente camino en el árbol de decisiones:

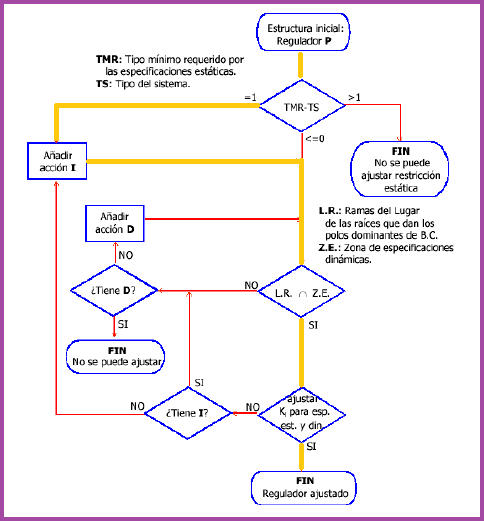Paso cuatro: ajustamos los parámetros del regulador.

Nuestro regulador tendrá una estructura PI = K*(z - a)/(z - 1)

En este caso la “a” la asignamos por cancelación, con lo que valdrá 0.95

De este modo la ecuación característica tendrá la siguiente forma:

Ecuacion caracteristica del ejemplo

El “z - 0.95” se despejan y nos queda que la ecuación característica es:

1 + (0.0024*K)/(z - 1)

Para facilitar calculos, tomamos por K_L=0.0024*K

Y ajustamos la K_L con el criterio del modulo despejando la ecuación característica, obtenemos la siguiente expresión:

|K_L| = |z – 1|

Particularizamos, para cuando la z vale 0.81 (que es el modulo del punto de especificaciones “z = 0.8 ± 0.17j”) y obtenemos que K_Lvale 0.183

Sustituyendo en la formula anterior: K_L=0.0024*K tenemos que la K vale 75.54

Es decir que nuestro PI final es:

PI = 75.54(z - 0.95)/(z - 1)

Paso cinco: Validarlo con el simulador.

En este caso lo validaríamos con el xcos de Scilab, y nos da algo similar a esto:

Simulación

Como vemos, no hay nada de sobreoscilación, además el tiempo de establecimiento es menor de 2 segundos y el error de posición es cero.

Hemos obtenido un regulador, que cumple nuestras especificaciones, y que nos controla el sistema. Ahora solo faltaria el paso ultimo, que es la implementacion de este regulador a la realidad, y ver si funciona.