

Para este tema es muy importante recordar los temarios de: lugar de las raíces, error en régimen permanente y especificaciones de un sistema; dado que en este tema se usaran bastante. |
| Bien, el PID consta
de una estructura con tres parámetros ajustables. La parte P, la parte I y la
D. La parte P es la más simple. La señal de control es proporcional al error
con el constante proporcional Kp. Esta constante determina la velocidad con la
que el regulador eliminará el error. En cuanto a la parte integral, la Ki
determina la magnitud de la influencia de la parte integral. Esto afecta en que
cuanto mas parte integral se tiene el regulador crece mientras la señal de
salida es menor que la señal de referencia(al contrario si es menor). En cuanto
a la parte derivativa, tiene en cuenta cambios del error. La constante Kd
determina la magnitud de neutralización y hace al sistema más estable pero a
cambio más lento. |
| El total da la
siguiente función discreta: |
 |
| La de arriba es la
función en función del tiempo, y la de abajo la que nos interesa: en discreto.
Para poder diseñar un PID deberemos seguir los siguientes pasos: |
| 1) Dibujar el lugar de las raíces de nuestro proceso G(z) |
| 2) Pasar las especificaciones al plano discreto (visto en
el tema de especificaciones de un sistema) |
|
3) Seleccionar la estructura de nuestro PID. Nuestro PID puede ser un P, PD, PI o PID. Es decir, podemos seleccionar las partes que le hacen falta, y no ponerlas todas. La importancia de ponerle solo lo que necesitamos erradica en que estaríamos quizás si usamos un PID entero en el caso de usar solo un P estaremos usando cosas que no necesitamos. El saber elegir adecuadamente entre un P y PID esta en el siguiente árbol de decisión: |
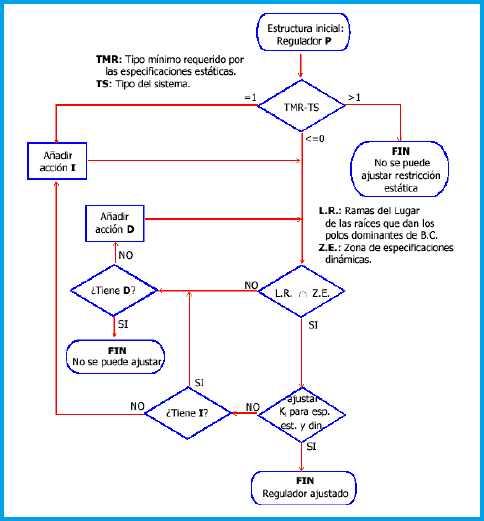 |
| Este árbol de decisión se explica
del siguiente modo. En un principio siempre aplicamos parte P. El primer paso
es el TMR-TS. Esto quiere decir: cantidad de polos en “z=1” menos los que
necesito. Por ejemplo si nuestro sistema Gp(z) tiene un polo en z=1 y
necesitamos que el error de posición sea cero, el TMR-TS será uno menos uno y
tendremos como resultado cero y continuaríamos hacia abajo hasta llegar al
cuadro L.R. ∩ Z.E. Si la resta TMR-TS da 1 deberemos añadir acción integral, y
una vez añadida seguiremos hasta el cuadro L.R. ∩ Z.E. Si el TMR-TS da mayor
que uno, el regulador no es viable. |
| El cuadro L.R. ∩ Z.E significa
que si nuestra zona de especificaciones corta con nuestro lugar de las raíces
podremos seguir adelante. Si no se cumple habrá que añadir acción derivativa
para que el lugar de las raíces se corte con la zona de especificaciones. |
| Una vez echo todo esto, y añadido
o no parte integral y derivativa, ajustamos una K dentro de la zona de
especificaciones y del lugar de las raíces, y nuestro regulador estará
ajustado. |
| 4) Ajustamos
los parámetros del regulador. En caso del P se elige la K por el criterio del
modulo. En el PI el cero se elige con el criterio del 1/10 o con cancelación y la K con el
criterio del modulo. En el PD el cero se elige con el criterio del argumento, y
la K con el criterio del modulo. Y el PID como el PI y el PD juntos. |
| 5) Se
valida el regulador con un simulador |
| 6) Se
simula el regulador en la vida real |
| A
continuación mostraremos unos cuantos ejemplos de como realizar
reguladores PID. Los reguladores algebraicos no mostraremos ejemplos,
puesto que son muy costosos de realizar, y cada vez más están en
desuso. Y con esto, daremos por finalizada esta unidad didactica. A
continuación hay un ejemplo de como diseñar un PID con un proceso
sencillo. |
 |
|
 |
 |
 |
|
 |
|