

| En cuanto al diseño
de los reguladores, los PID son los más utilizados por ser muy sencillos (tan
solo tienen tres parámetros ajustables) tanto como de utilizar como de
implementar. Sin embargo los PID están limitados para especificaciones muy
estrictas. Los reguladores algebraicos permiten mitigar los problemas del PID,
pero conllevan más problemas, como por ejemplo oscilaciones ocultas. A
continuación mencionaremos los cuatro reguladores algebraicos más importantes: asignación
de polos, cancelación, tiempo finito y tiempo mínimo. |
| -Asignación de
polos: Tratan que los polos de la función de transferencia directa
coincidan con las especificaciones que nosotros deseamos, y además cancela ceros, siempre que sean estables. |
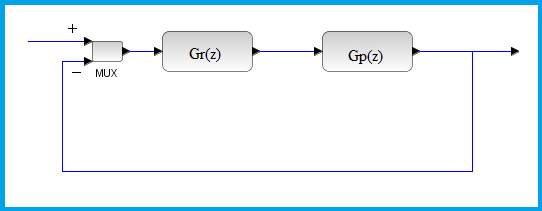
| Si la ecuación característica
es 1 + Gr(z)*Gp(z) = 0 |
 |
|
Si asignamos a Gp(z) =
B(z)/A(z) y a Gr(z) = Q(z)/P(z) |
| La ecuación característica
se nos queda como: 1 + [B(z)/A(z)]*[Q(z)/P(z)] o lo que es lo mismo: A(z)*P(z)
+ B(z)*Q(z) = 0 |
| Lo que nos restara es
encontrar los polinomios incógnita P(z) y Q(z) |
|
Esto se resuelve igualando coeficiente a coeficiente los polinomios que aparecen en la ecuación característica, ajustándolos con las especificaciones discretizadas que hayamos elegido u obtenido. Obviamente habrá solución única si el número de ecuaciones es igual al número de incógnitas.
|
| -Cancelación: Se
basan en la cancelación dinámica del proceso para sustituirla por una nueva
dada por la función de transferencia directa del sistema. Se cancelan tantos polos como ceros estables. |
|
| Despejando la
expresión que vemos para aislar Gr(z), que es el regulador que deseamos
obtener, tenemos esta expresión: |
 |
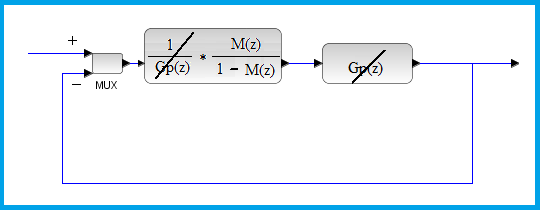
| Pero queda mucho más claro viéndolo en el bucle de
control: |
 |
| -Tiempo mínimo:
Ante cualquier referencia pretende anular la señal de error en régimen
permanente
en un número mínimo de periodos de muestreo. Cancela polos y ceros que
sean estables. Además elimina el error de posición y el de velocidad.
Tiene el inconveniente de poder presentar oscilaciones ocultas.
Para solucionarlo se recomienda no cancelar los ceros del sistema. |
| -Tiempo finito:
Son muy similares a la asignación de polos. Estos asignan los polos de
bucle
cerrado en el origen del plano Z. Cancelan los polos estables del
sistema, y anulan el error de posición de velocidad. No obstante no
cancelan los ceros. |
 |
 |
 |
|
 |
|