Para poder ver mejor las diferencias entre los retenedores que hemos mencionado en el tema de reconstrucción, vamos a poner, con Matlab, tres ejemplos: un retenedor de orden cero, otro de primer orden y por ultimo un retenedor poligonal.

EJEMPLO RETENEDOR ORDEN CERO
En primer lugar en el entorno de simulink ponemos el bloque del retenedor del orden cero:
Simulink retenedor de orden cero

Comparando las dos señales podemos ver como se reconstruye una imagen con un retenedor de orden cero en la siguiente secuencia de imagenes:
Reconstrucción por un orden cero
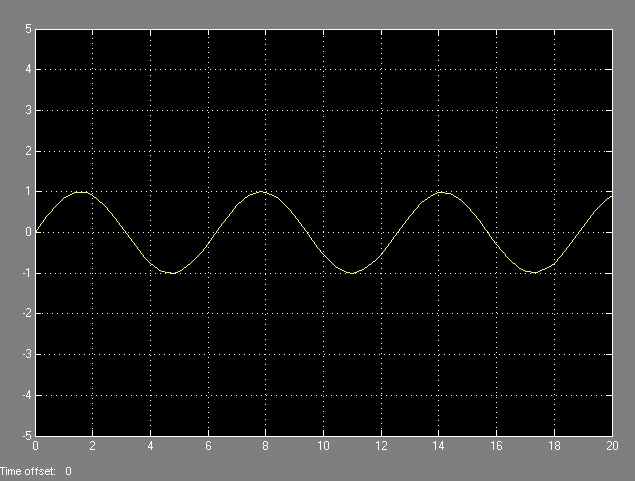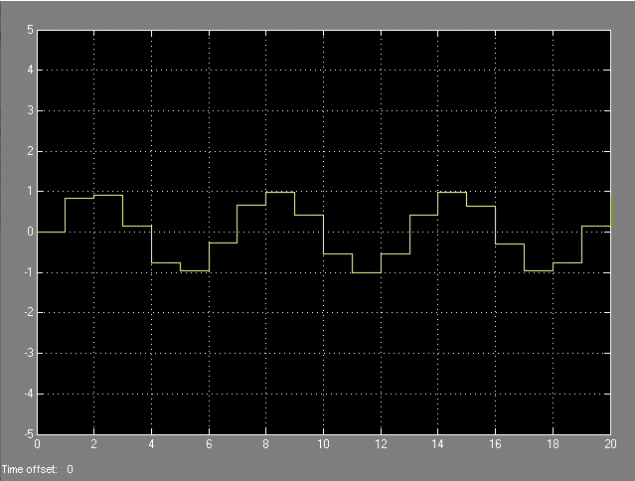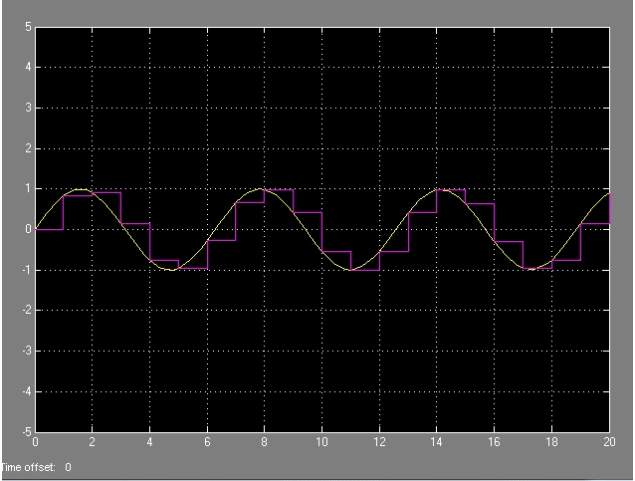Como hemos mencionado, la reconstrucción no es exacta, pero puede ser una buena aproximación si lo que nos interesa es la rapidez.


EJEMPLO RETENEDOR PRIMER ORDEN
Como en el ejemplo anterior empezamos poniendo el bloque adecuado antes, y tenemos lo siguiente:
Simulink retenedor de primer orden
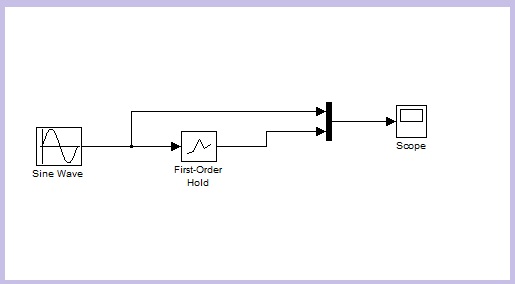Comparando las dos señales, la original junto a la muestreada, podemos ver como se reconstruye una imagen con un retenedor de primer orden en la siguiente secuencia de imagenes:
Reconstrucción por un primer orden


EJEMPLO RETENEDOR POLIGONAL
Como hemos echo en los anteriores ejemplos hacemos el simulink del retenedor poligonal, incluyendo tras un retenedor de orden cero la función: (1/T)/[(s+1)*T]:
Simulink retenedor poligonal
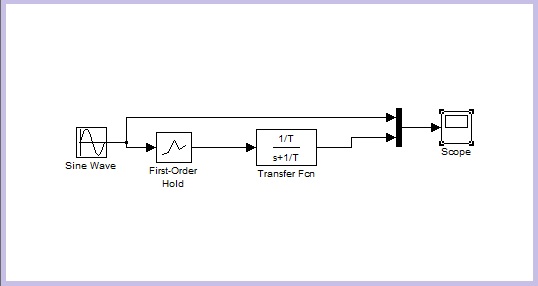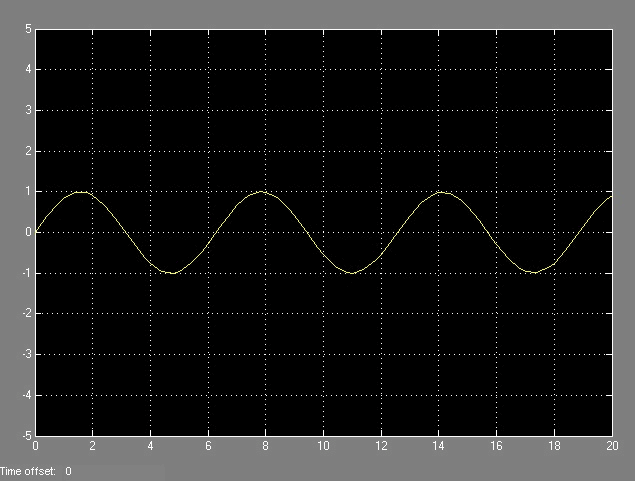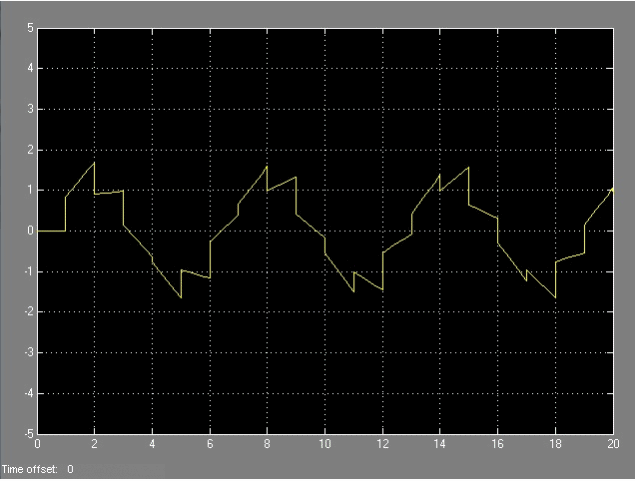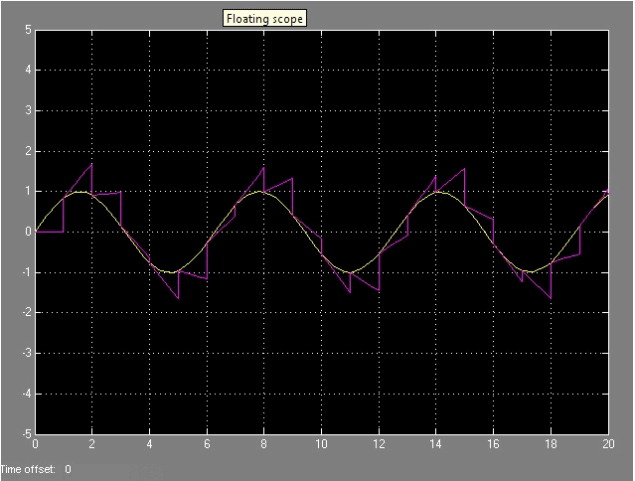
Comparando las dos señales podemos ver como se reconstruye una imagen con un retenedor poligonal en esta secuencia de imagenes:
Reconstrucción por un poligonal
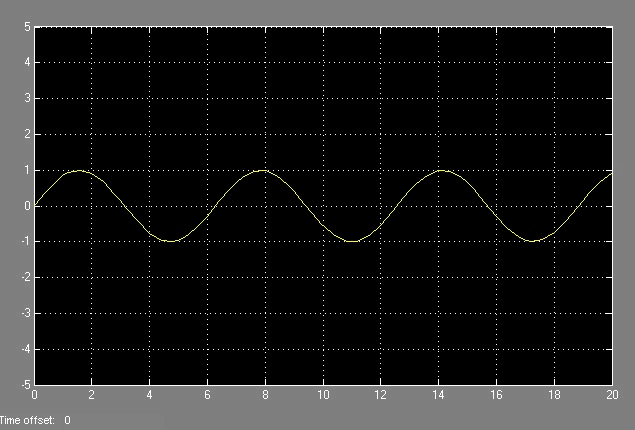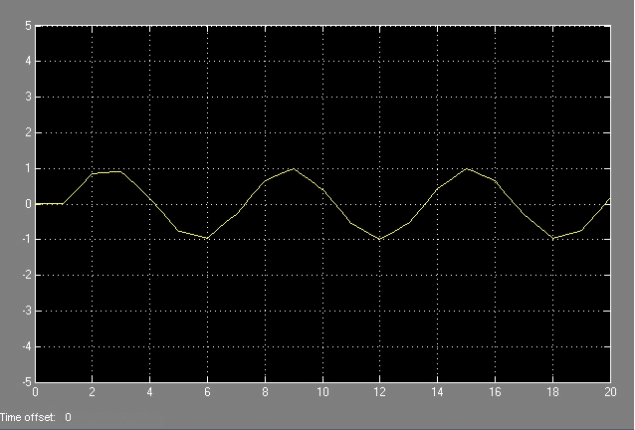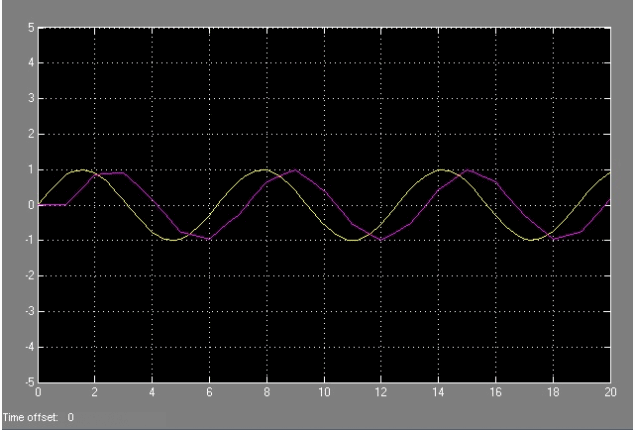Como vemos, de los tres el mejor es el retenedor poligonal, pero tiene el problema que se aprecia en esta ultima sencuencia. Al superponer las dos imagenes vemos que se obtiene un retraso, y la señal no sale al mismo tiempo, puesto que tarda más en calcularse. Ademas tiene el problema añadido de que requiere una elaboración más compleja. A priori el que mas se usa siempre es el retenedor de orden cero. No obstante, si necesitamos precisión, el retenedor poligonal seria el más adecuado.

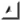Reconstrucción

Inicio de página

Inicio